
20、(2006陕西卷)
已知函数f(x)=x3-x2+ + , 且存在x0∈(0, ) ,使f(x0)=x0.
(I)证明:f(x)是R上的单调增函数;设x1=0, xn+1=f(xn); y1=, yn+1=f(yn), 其中 n=1,2,……
(II)证明:xn<xn+1<x0<yn+1<yn;
(III)证明: <
19、(2006山东卷)
设函数f(x)=ax-(a+1)ln(x+1),其中a -1,求f(x)的单调区间。
-1,求f(x)的单调区间。
18、(2006全国II)
设函数f(x)=(x+1)ln(x+1),若对所有的x≥0,都有f(x)≥ax成立,求实数a的取值范围.
17、(2006全国卷I)
已知函数 。
。
(Ⅰ)设 ,讨论
,讨论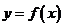 的单调性;
的单调性;
(Ⅱ)若对任意 恒有
恒有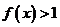 ,求
,求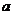 的取值范围。
的取值范围。
16、(2006辽宁卷)
已知函数f(x)= ,其中a , b , c是以d为公差的等差数列,,且a>0,d>0.设
,其中a , b , c是以d为公差的等差数列,,且a>0,d>0.设 [1-
[1- ]上,
]上, ,在
,在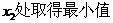 ,将点
,将点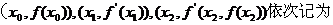 A, B, C
A, B, C
(I)求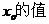
(II)若⊿ABC有一边平行于x轴,且面积为 ,求a ,d的值
,求a ,d的值
15、(2006湖南卷)
已知函数 ,数列{
,数列{ }满足:
}满足:
证明:(ⅰ) ;
(ⅱ)
;
(ⅱ) .
.
14、(2006湖北卷)
设 是函数
是函数 的一个极值点。
的一个极值点。
(Ⅰ)、求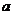 与
与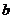 的关系式(用
的关系式(用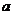 表示
表示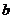 ),并求
),并求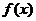 的单调区间;
的单调区间;
(Ⅱ)、设 ,
, 。若存在
。若存在 使得
使得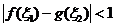 成立,求
成立,求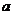 的取值范围。
的取值范围。
13、(2006广东卷)
设函数 分别在
分别在 处取得极小值、极大值.
处取得极小值、极大值. 平面上点
平面上点 的坐标分别为
的坐标分别为 、
、 ,该平面上动点
,该平面上动点 满足
满足 ,点
,点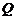 是点
是点 关于直线
关于直线 的对称点.求
的对称点.求
(I)求点 的坐标;
的坐标;
(II)求动点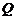 的轨迹方程.
的轨迹方程.
12、(2006福建卷)
已知函数f(x)=-x +8x,g(x)=6lnx+m
+8x,g(x)=6lnx+m
(Ⅰ)求f(x)在区间[t,t+1]上的最大值h(t);
(Ⅱ)是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有三个不同的交点?若存在,求出m的取值范围;,若不存在,说明理由。
10、(2006江苏卷)
已知 函数
函数
(Ⅰ)当a=2时,求使f(x)=x成立的x的集合;
(Ⅱ)求函数y=f (x)在区间[1,2]上的最小值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com