
 例题6.一物体在斜面上以一定的初速度向上运动,斜面的倾角
例题6.一物体在斜面上以一定的初速度向上运动,斜面的倾角 可在
可在 -
- 之间变化,设物体所能达到的最大位移
之间变化,设物体所能达到的最大位移 与斜面倾角
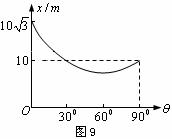
与斜面倾角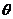 之间的关系如图9所示,试求当
之间的关系如图9所示,试求当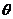 多大时
多大时 有最小值?这个最小值是多大?
有最小值?这个最小值是多大?
解析:设物体的初速度为 ,在斜面上滑行时的加速度大小为
,在斜面上滑行时的加速度大小为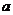 ,则
,则


当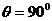 时,物体做竖直上抛运动,由图可知上升的最大高度为
时,物体做竖直上抛运动,由图可知上升的最大高度为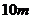 ,则
,则

所以 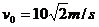
当 时,物体沿水平面作匀减速直线运动,由图可知此时滑行的最大距离为
时,物体沿水平面作匀减速直线运动,由图可知此时滑行的最大距离为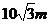 ,则
,则
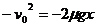
故 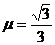
将 和
和 的值代入上面
的值代入上面 的表达式,在利用数学知识整理可得当
的表达式,在利用数学知识整理可得当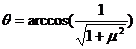 时,位移
时,位移 有最小值,将
有最小值,将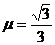 代入得
代入得
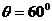
所以物体最大位移的最小值为
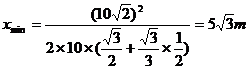
命题解读:应用数学知识解决物理问题是高考考察的能力之一,除本题应用的三角函数变换以外,还有如数学归纳法、二次函数极值等都是解决物理问题的强有力工具,不论是在力学还是电学,好多的物理应用题中都有所涉及,高考计算题中也多次出现,平常学习时请注意掌握。
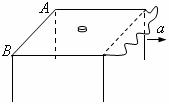 例题5.如图8所示,一小圆盘静止在桌布上,位于方桌水平面的中央,桌布的一边与方桌的
例题5.如图8所示,一小圆盘静止在桌布上,位于方桌水平面的中央,桌布的一边与方桌的 边重合,已知盘与桌布间的动摩擦因数为
边重合,已知盘与桌布间的动摩擦因数为 ,盘与桌面间的动摩擦因数为
,盘与桌面间的动摩擦因数为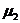 ,现突然以恒定加速度
,现突然以恒定加速度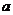 将桌布抽离桌面,加速度方向是水平的且垂直于
将桌布抽离桌面,加速度方向是水平的且垂直于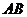 ,若圆盘最后没从桌面上掉下,则加速度
,若圆盘最后没从桌面上掉下,则加速度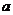 应满足的条件是什么?(以
应满足的条件是什么?(以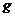 表示重力加速度)
表示重力加速度)
|
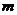 ,方桌边长为
,方桌边长为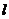 ,圆盘在桌布上时,由牛顿第二定律得
,圆盘在桌布上时,由牛顿第二定律得
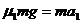
桌布抽出后,圆盘在桌面上时,又有

设圆盘刚离开桌布时的速度为 ,移动的位移为
,移动的位移为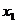 ,离开桌布后在桌面上再运动
,离开桌布后在桌面上再运动 后便停下,由匀变速直线运动规律公式,得
后便停下,由匀变速直线运动规律公式,得
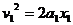
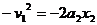
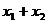 ≤
≤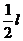
设桌布从圆盘下抽出所经历的时间为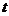 在这段时间内桌布发生的位移为
在这段时间内桌布发生的位移为 ,则
,则

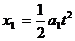
解以上各式,得
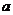 ≥
≥
命题解读:本题是一道牛顿第二定律的应用题,解题的其中一个关键就是要分析出圆盘在两个运动阶段的加速度不同;另一个关键则是要分析出圆盘布从桌面掉下的临界条件是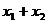 ≤
≤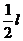 ,这才是解题的难点。
,这才是解题的难点。
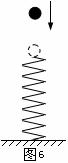 例题4.如图6所示,一个小球从直立在地面上的轻弹簧的上方某处自由落下,接触弹簧后将弹簧压缩,在压缩的整个过程中,弹簧均为弹性形变,那么当弹簧的压缩量最大时
例题4.如图6所示,一个小球从直立在地面上的轻弹簧的上方某处自由落下,接触弹簧后将弹簧压缩,在压缩的整个过程中,弹簧均为弹性形变,那么当弹簧的压缩量最大时
 .小球所受合力最大,但不一定大于重力值
.小球所受合力最大,但不一定大于重力值
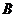 .小球的加速度最大,且一定大于重力加速度
.小球的加速度最大,且一定大于重力加速度
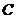 .小球的加速度最大,有可能小于重力加速度
.小球的加速度最大,有可能小于重力加速度
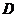 .小球所受弹力最大,但不一定大于重力值
.小球所受弹力最大,但不一定大于重力值
解析:本题的四个选项中,要求对两个量的大小进行判断,一个是力,另一个是加速度。根据牛顿第二定律可知,加速度由力决定,所以按照通常的做法,只要解决了弹簧被压缩过程中弹力大小的变化情况的判断,就可以很顺利的进行小球加速度大小的判断,实际上是这样吗?当弹簧的压缩量最大时,弹簧的弹力究竟和重力是个什么样的关系?
小球从弹簧上端的某处自由落下,以某一速度刚接触弹簧时,只受重力作用,从而此时小球的加速度为重力加速度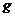 。小球一旦开始压缩弹簧,弹簧便会产生弹力,但开始时弹力很小,随着压缩量逐渐增大,弹簧产生的弹力也会逐渐增大,当弹力增大到和重力相等时,合力为零,加速度也为零,此时小球的速度达到最大值。这一时刻过后,小球还会继续压缩弹簧,弹力也将会大于小球的重力,当小球的速度减小到零时,弹簧被压缩到最短,弹力最大。分析到此,好象只能判断出弹簧被压缩到最短时,弹簧的弹力最大(此时小球所受合力也是最大的),并且一定大于小球的重力,从而答案
。小球一旦开始压缩弹簧,弹簧便会产生弹力,但开始时弹力很小,随着压缩量逐渐增大,弹簧产生的弹力也会逐渐增大,当弹力增大到和重力相等时,合力为零,加速度也为零,此时小球的速度达到最大值。这一时刻过后,小球还会继续压缩弹簧,弹力也将会大于小球的重力,当小球的速度减小到零时,弹簧被压缩到最短,弹力最大。分析到此,好象只能判断出弹簧被压缩到最短时,弹簧的弹力最大(此时小球所受合力也是最大的),并且一定大于小球的重力,从而答案 是错误的。至于弹簧的弹力到底比小球的重力大多少?合力是否“一定大于重力”?“加速度一定大于重力加速度”?答案不是一下子就能判断出来的,甚至解决不了!
是错误的。至于弹簧的弹力到底比小球的重力大多少?合力是否“一定大于重力”?“加速度一定大于重力加速度”?答案不是一下子就能判断出来的,甚至解决不了!
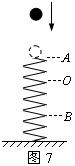 这时,就应该改变思维方式,把“由力判断加速度”改作“对加速度直接判断”。根据学过的弹簧振子模型,当弹簧振子在最大位移处时,加速度最大,并且关于平衡位置对称的位置上,加速度、速度和位移等都有对称关系。此题中,弹簧被压缩到最短的位置
这时,就应该改变思维方式,把“由力判断加速度”改作“对加速度直接判断”。根据学过的弹簧振子模型,当弹簧振子在最大位移处时,加速度最大,并且关于平衡位置对称的位置上,加速度、速度和位移等都有对称关系。此题中,弹簧被压缩到最短的位置 ,就是“振子”的最大位移处;小球受力平衡,即其加速度为零的位置就是“振子”的平衡位置
,就是“振子”的最大位移处;小球受力平衡,即其加速度为零的位置就是“振子”的平衡位置 处;而和小球刚接触弹簧位置
处;而和小球刚接触弹簧位置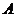 关于平衡位置对称的位置,应该在
关于平衡位置对称的位置,应该在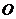 和
和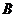 之间,如图7 所示。因为小球刚接触弹簧时其加速度为重力加速度,
之间,如图7 所示。因为小球刚接触弹簧时其加速度为重力加速度,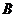 位置处的加速度又是最大的,故
位置处的加速度又是最大的,故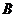 处的加速度大于重力加速度,本题的正确答案是
处的加速度大于重力加速度,本题的正确答案是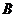 。
。
命题解读:分析本题时,如果一个思路走下去可能就是死胡同一条,可巧妙的利用了弹簧振子模型后,问题的解决变得既简洁又准确,平常的学习中就要多类比、多联想、多变换,使平常学过的知识能够被灵活的运用。
2.正交分解法:
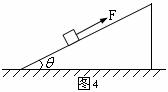 例题3.如图4所示,在倾角为
例题3.如图4所示,在倾角为 的足够长的斜面上,有一质量
的足够长的斜面上,有一质量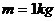 的物体,物体与斜面之间的动摩擦因数为
的物体,物体与斜面之间的动摩擦因数为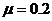 ,物体受到沿斜面向上的拉力
,物体受到沿斜面向上的拉力 的作用,并从静止开始运动,经过
的作用,并从静止开始运动,经过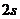 绳子突然断了,试求:断绳后多长时间物体的速度大小达到
绳子突然断了,试求:断绳后多长时间物体的速度大小达到 ?
?
解析:在最初的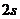 内,物体在
内,物体在 的拉力作用下,从静止开始沿斜面做匀加速直线运动,据受力分析(如图5所示),根据牛顿第二定律和物体的平衡条件可知
的拉力作用下,从静止开始沿斜面做匀加速直线运动,据受力分析(如图5所示),根据牛顿第二定律和物体的平衡条件可知
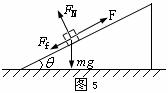
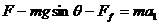 ①
①
 ②
②
且  ③
③
由①--③式可得
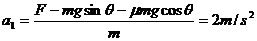
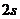 末断绳,物体的瞬时速度达到
末断绳,物体的瞬时速度达到
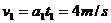
从绳子断开,物体继续沿斜面向上运动达到最高点速度为零的过程,设加速度为 ,经过的时间为
,经过的时间为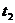 ,则
,则
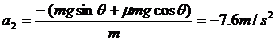
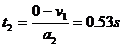
再设物体从最高点沿斜面下滑过程中加速度为 ,到物体的速度大小达到
,到物体的速度大小达到 所用时间为
所用时间为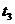 ,则由牛顿第二定律和运动学的基本公式,得
,则由牛顿第二定律和运动学的基本公式,得
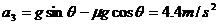

综上所述,从断绳到物体速度达到 所经历的总时间为
所经历的总时间为
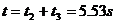
思考:如果题目要求“断绳后多长时间物体的速度大小达到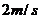 ?”呢?这个速度对应的时间因该有两个,即两个解,一个是从断绳到速度减小到
?”呢?这个速度对应的时间因该有两个,即两个解,一个是从断绳到速度减小到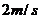 经过的时间,另一个则是从断绳到物体反向加速到
经过的时间,另一个则是从断绳到物体反向加速到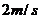 。不妨求一下试试?
。不妨求一下试试?
命题解读:在物体受力较多(3个以上)的情况下,受力分析完了以后,一般采取的都是正交分解的办法,即沿两个互相垂直的方向将力进行分解,然后列出相对应的方程。正交分解在处理多力问题时有它的优越性,需要解决的问题就是取“怎样的两个相互垂直的方向”?一般情况下,选取的其中一个方向就是物体的运动方向,另一个则是和物体运动方向垂直的方向。
1.合成法:
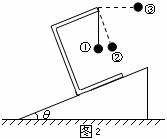 例题2.如图2所示,一倾角为
例题2.如图2所示,一倾角为 的斜面上放一滑块,滑块上固定一支架,支架末端用细绳悬挂一小球,滑块在斜面上下滑时小球与滑块相对静止一起运动,当细线:①沿竖直方向、②与斜面方向垂直、③沿水平方向,试求上述三种情况下滑块下滑的加速度.
的斜面上放一滑块,滑块上固定一支架,支架末端用细绳悬挂一小球,滑块在斜面上下滑时小球与滑块相对静止一起运动,当细线:①沿竖直方向、②与斜面方向垂直、③沿水平方向,试求上述三种情况下滑块下滑的加速度.
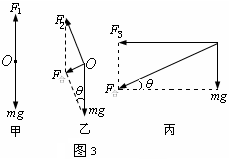 解析:由题意知,小球与滑块的加速度相同,都是沿斜面向下的。对几种情况下的小球进行受力分析,分别如图3中的甲、乙和丙所示。
解析:由题意知,小球与滑块的加速度相同,都是沿斜面向下的。对几种情况下的小球进行受力分析,分别如图3中的甲、乙和丙所示。
①图甲中,细线对小球的拉力 和小球的重力
和小球的重力 都在竖直方向上,故不可能有加速度,
都在竖直方向上,故不可能有加速度,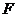 =
= ,所以
,所以 ,说明滑块沿斜面匀速下滑。
,说明滑块沿斜面匀速下滑。
②图乙中,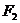 和
和 的合力方向就是加速度的方向,即沿斜面方向,做出平行四边形,求得合力为
的合力方向就是加速度的方向,即沿斜面方向,做出平行四边形,求得合力为
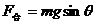
由牛顿第二定律,得
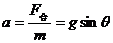
即加速度的大小为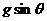 ,方向沿斜面向下。
,方向沿斜面向下。
③图丙中,细绳产生的拉力方向如图所示,故小球所受的合力为
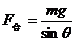
所以,此时的加速度为

方向沿斜面向下。
命题解读:这道题的解题过程并不复杂,但它反映了利用牛顿第二定律解题的一种类型,即在物体受力不太多的情况下,分析完物体的受力情况后,一般是利用平行四边形定则求出合力,然后利用牛顿第二定律求出加速度。
4.DNA分子一条链中(A+T)/(C+G)的比值等于其互补链和整个DNA分子中该种比例的比值。
3. DNA分子一条链中(A+G)/(C+T)的比值的倒数等于其互补链中该种碱基的比值。
2.在双链DNA分子中,互补的两碱基之和(如A+T或C+G)占全部碱基的比等于其任何一条单链中该种碱基比例的比值,且等于其转录形成的mRNA中该种比例的比值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com