
8.已知偶函数y=f(x)在[-1,0]上为单调递减函数,又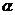 、
、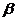 为锐角三角形的两内角,则( )
为锐角三角形的两内角,则( )
A.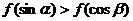 B.
B.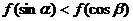 C.
C.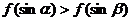 D.
D.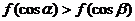
7.已知向量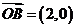 ,向量
,向量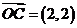 ,向量
,向量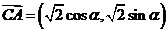 ,则向量
,则向量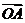 与
与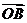 的夹角的范围为( )A.
的夹角的范围为( )A.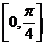 B.
B.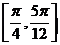 C.
C. 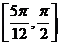 D.
D.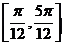
6. 已知向量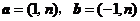 ,若
,若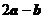 与
与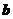 垂直,则
垂直,则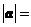 ( )
( )
A.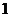 B.
B.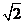 C.
C.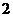 D.4
D.4
5. 已知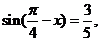 则
则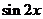 的值为( )
的值为( )
A.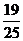 B.
B.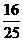 C.
C.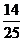 D.
D.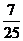
4.设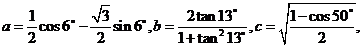 则有( )
则有( )
A.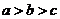 B.
B.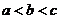 C.
C.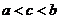 D.
D.
3.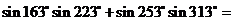 ( )
( )
A.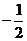 B.
B.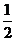 C.
C.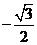 D.
D.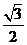
2.设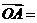
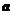 ,
,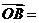
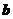 ,
,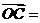
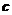 ,当
,当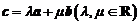 ,且
,且 时,点
时,点 在( )
在( )
A.线段AB上 B.直线AB上 C.直线AB上,但除去A点 D.直线AB上,但除去B点
1. ( )
( )
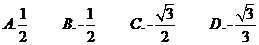
例题8.如图12所示,长为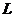 、质量为
、质量为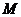 的圆柱形木棒竖直放置,在其顶部套有一质量为
的圆柱形木棒竖直放置,在其顶部套有一质量为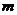 的薄铁环,当棒和环有相对运动时,棒和环之间有大小恒为
的薄铁环,当棒和环有相对运动时,棒和环之间有大小恒为 (
(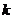 >
> )的摩擦力。现突然在棒的下端给棒一个很大的冲击力,使棒瞬间具有竖直向上的初速度
)的摩擦力。现突然在棒的下端给棒一个很大的冲击力,使棒瞬间具有竖直向上的初速度 ,试求:
,试求:
⑴若要使铁环在木棒落地之前不滑离木棒,此木棒的长度不能少于多少?
⑵设木棒足够长,求棒上升的最大高度?
解析:⑴经过分析可知,为使铁环在木棒落地之前不滑离木棒,只需铁环与木棒具有向上的共同速度时不滑离木棒即可。
设铁环的加速度大小为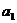 ,由于
,由于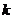 >1,故方向向上;木棒的加速度大小为
>1,故方向向上;木棒的加速度大小为 ,方向向下。则有
,方向向下。则有
对于铁环 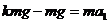
对于木棒 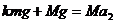
木棒相对于铁环的加速度为
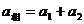
解以上几式得
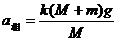
再由匀变速直线运动规律公式得
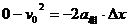
解得 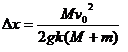
木棒的长度为
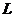 ≥
≥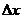
所以木棒的最小长度为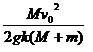
⑵铁环和木棒的速度相等时,对于铁环和木棒分别有
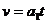
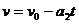
解得 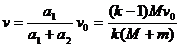
设此时木棒上升的高度为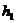 ,以木棒的初速度方向为正方向,则
,以木棒的初速度方向为正方向,则
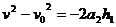
解得 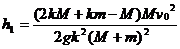
命题解读:本题涉及到物体的受力分析、牛顿第二定律、运动学规律和相对运动等规律,是典型的综合问题,重在考查灵活运用牛顿定律和运动学规律求解关联问题的能力,这也是高考综合分析计算题命题的重点和热点。
 例题7.用质量为
例题7.用质量为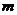 、长度为
、长度为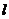 的绳子沿光滑水平面拉动质量为
的绳子沿光滑水平面拉动质量为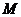 的物体,在绳子的一端施加的水平拉力为
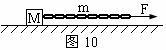
的物体,在绳子的一端施加的水平拉力为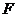 ,如图10所示,试求:
,如图10所示,试求:
⑴物体与绳子的加速度;
⑵绳子中各处张力的大小(假定绳子的质量分布均匀,下垂可以忽略)。
解析:⑴以物体和绳子为研究对象,根据牛顿第二定律得
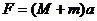
所以
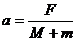
方向与力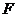 的方向是相同的,即水平向右。
的方向是相同的,即水平向右。
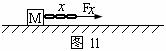 ⑵再以物体和靠近物体的长度为
⑵再以物体和靠近物体的长度为 的一部分绳子为研究对象如图11所示。根据牛顿第二定律,得
的一部分绳子为研究对象如图11所示。根据牛顿第二定律,得
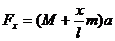
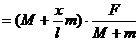
由上式可知,绳子中各处张力的大小是不同的,离物体越近的地方张力越小,当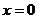 时,绳子施加于物体上的力为
时,绳子施加于物体上的力为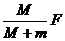 。
。
命题解读:一般情况下我们研究的都是轻绳,其质量是可以忽略不计的,只考虑它由于发生弹性形变而产生的弹力,从这道题可以看出,绳子的质量不能忽略时,是可以把它和其它的物体一样对待的;整体分析法也不是万能的,隔离法乃是解决牛顿运动定律问题的基本方法,在分析整体内部各部分之间的相互作用时必须应用隔离法,在解决具体问题时要具体分析,两种方法要灵活运用。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com