
3.利用三角形知识巧解多力的合力
 例题5.如图16所示,
例题5.如图16所示,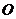 点为三角形
点为三角形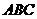 的重心,并且有三个共点力
的重心,并且有三个共点力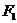 、
、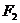 和
和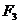 作用在
作用在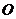 点,试证明三个力的合力为零。
点,试证明三个力的合力为零。
解析:如图17所示,将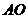 延长,交
延长,交 于
于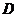 点,并继续延长至
点,并继续延长至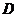 点,截取
点,截取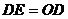 ,因为
,因为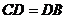 (三角形重心的性质),所以,连接
(三角形重心的性质),所以,连接 、
、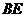 得到的四边形
得到的四边形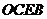 为平行四边形,从而力
为平行四边形,从而力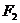 、
、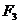 的合力等于
的合力等于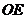 长度对应的力。而
长度对应的力。而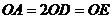 ,所以三个力
,所以三个力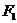 、
、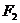 和
和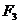 的合力为零。
的合力为零。
思路点拨:求解三个以上力的合成问题称为多力合成。多力合成是力的合成运算中较为复杂的情况,求解多个力的合力,常用“正交分解法”、“特殊规律法”和“几何法”等,其中“几何法”是这几种方法中特别灵活、与数学知识的关系较为密切的,运用这种方法最为关键的是挖掘出问题的几何特点。
2.图解法求解分力的最小值
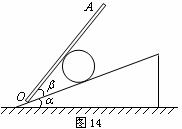 例题4.如图14所示,质量为
例题4.如图14所示,质量为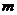 的光滑小球被夹在倾角为
的光滑小球被夹在倾角为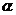 的斜面和挡板
的斜面和挡板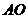 之间,试分析挡板
之间,试分析挡板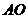 与斜面之间的倾角
与斜面之间的倾角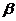 多大时,挡板
多大时,挡板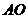 所受的压力最小?
所受的压力最小?
解析:以小球为研究对象,分析其受力情况如图15所示。小球所受的重力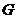 产生了两个作用效果:使小球靠紧挡板和紧压在斜面上,所以将重力
产生了两个作用效果:使小球靠紧挡板和紧压在斜面上,所以将重力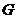 分解为两个分力
分解为两个分力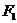 和
和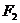 。
。
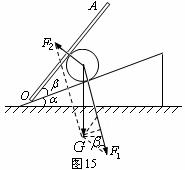 从图15可以看出,当挡板与斜面的夹角
从图15可以看出,当挡板与斜面的夹角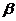 由图示位置变化时,根据平行四边形的变形,就可以判断出两个分力的变化:分力
由图示位置变化时,根据平行四边形的变形,就可以判断出两个分力的变化:分力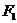 的大小改变,但方向是不变的,始终与斜面垂直,而
的大小改变,但方向是不变的,始终与斜面垂直,而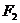 的大小和方向均发生改变,当分力
的大小和方向均发生改变,当分力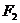 的方向变到与
的方向变到与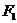 垂直,即
垂直,即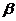
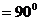 时,挡板
时,挡板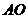 所受的压力最小,最小值为
所受的压力最小,最小值为
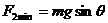
思路点拨:虽然题目问的是挡板所受的压力情况,但若直接以挡板为研究对象,其所受的其它力又不知道,将无法进行讨论。因小球的质量已知,选择它为研究对象,再利用力的分解和牛顿第三定律的知识,就可以得出结论。
1.摩擦力大小的计算----二面角的应用
通常见到的斜面问题,斜面的倾角是已知的,但有时要利用几何知识进行求解,请看下面的例子:
 例题3.如图12所示,在水平桌面
例题3.如图12所示,在水平桌面 上放置一块正方形薄木板
上放置一块正方形薄木板 ,在木板的正中点放置一块质量为
,在木板的正中点放置一块质量为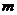 的木块。先以木板的
的木块。先以木板的 边为轴,将木板向上缓慢转动,使木板的
边为轴,将木板向上缓慢转动,使木板的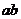 边与桌面的夹角为
边与桌面的夹角为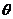 ;再接着以木板的
;再接着以木板的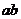 边为轴,将木板向上缓慢转动,使木板的
边为轴,将木板向上缓慢转动,使木板的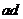 边与桌面的夹角为
边与桌面的夹角为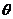 (
(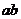 边与桌面的夹角
边与桌面的夹角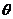 不变),在转动过程中,木块在木板上始终没有滑动。则转动以后木块受到的摩擦力的大小为多少?
不变),在转动过程中,木块在木板上始终没有滑动。则转动以后木块受到的摩擦力的大小为多少?
 解析:设经过两次旋转,最终正方形薄板与水平面之间成一定的夹角
解析:设经过两次旋转,最终正方形薄板与水平面之间成一定的夹角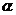 ,画出草图如图13所示。图中,边
,画出草图如图13所示。图中,边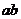 和
和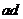 与水平面之间的夹角均为
与水平面之间的夹角均为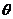 ,
, 为两条对角线
为两条对角线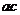 和
和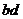 的交点,而
的交点,而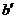 、
、 和
和 分别为
分别为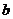 、
、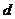 和
和 三点在水平面上的投影,则薄板与水平面之间的夹角
三点在水平面上的投影,则薄板与水平面之间的夹角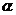 就是
就是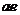 和
和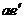 之间的夹角。设正方形的边长为
之间的夹角。设正方形的边长为 ,则由几何知识,得
,则由几何知识,得

所以,此时还静止在斜面上的木块所受到的摩擦力为

思路点拨:显然,解决旋转以后的正方形平面与水平面之间的二面角大小是解题的关键,这是一道利用数学知识解决物理问题的题目,只要解决了角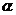 ,即通常做题时的斜面的倾角,后面的运算反而显得十分的简单,这也是这道题的一大特点。
,即通常做题时的斜面的倾角,后面的运算反而显得十分的简单,这也是这道题的一大特点。
最典型的,如弹簧类物体产生的弹力大小,根据胡克定律就可很快求出;但对于一般物体而言,还是要分析受力情况,利用平衡条件或动力学规律进行求解。
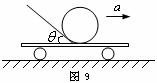 例题3.如图9所示,带斜面的小车在水平地面上,斜面倾角为
例题3.如图9所示,带斜面的小车在水平地面上,斜面倾角为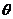 ,仅靠斜面有一质量为
,仅靠斜面有一质量为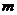 的光滑球,试求在下列状态下斜面对小球的弹力大小:
的光滑球,试求在下列状态下斜面对小球的弹力大小:
⑴小车向右匀速运动;
⑵小车向右以加速度 <
< )做匀加速直线运动;
)做匀加速直线运动;
⑶小车向右以加速度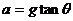 的加速度做匀加速直线运动。
的加速度做匀加速直线运动。
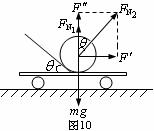 解析:对小球进行受力分析,如图10所示,将斜面对小球的支持力
解析:对小球进行受力分析,如图10所示,将斜面对小球的支持力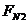 正交分解,则由平衡条件和牛顿第二定律,得
正交分解,则由平衡条件和牛顿第二定律,得
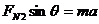 ①
①
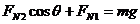 ②
②
由①、②两式,得
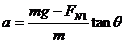 ③
③
由③式可以看出,当 时,
时, ,即此时的加速度
,即此时的加速度 就是小球刚好离开车的上表面所需要的最小加速度值,即临界值。
就是小球刚好离开车的上表面所需要的最小加速度值,即临界值。
⑴当小球向右匀速运动,即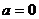 时,由①式得斜面对小球的弹力为
时,由①式得斜面对小球的弹力为

⑵当车运动的加速度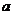 <
< 时,小球还压在车的表面上,此时的小球受力情况和图10是一样的,则由牛顿第二定律和几何知识,得
时,小球还压在车的表面上,此时的小球受力情况和图10是一样的,则由牛顿第二定律和几何知识,得
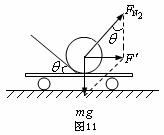
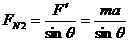
⑶当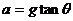 时,就是刚才所讨论的临界情况,即此时小球刚好离开车的表面,小球的受力情况如图11所示,则斜面对小球的弹力为
时,就是刚才所讨论的临界情况,即此时小球刚好离开车的表面,小球的受力情况如图11所示,则斜面对小球的弹力为
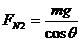
思路点拨:小车运动的加速度比较小时,小球和斜面、小车都有相互作用力,随着加速度的逐渐增大,求和车的上表面之间的压力逐渐减小,刚要离开小车的表面时,加速度达到一个特定的值 ,这个特定的值便是解决此题的关键。
,这个特定的值便是解决此题的关键。
2.根据物体的所处的状态,利用平衡条件或牛顿运动定律进行判断
有些物体(如杆)发生的形变并不明显,根据形变判断弹力方向非常困难,这时就要根据物体所处的状态进行判断。
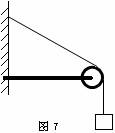 例题2.如图7所示,横梁的一端插在墙上,另一端固定一小的定滑轮,一轻质细绳跨过定滑轮,下面系一质量为
例题2.如图7所示,横梁的一端插在墙上,另一端固定一小的定滑轮,一轻质细绳跨过定滑轮,下面系一质量为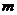 的小球,整个装置处于静止,试分析横梁对滑轮的弹力方向。
的小球,整个装置处于静止,试分析横梁对滑轮的弹力方向。
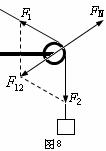 解析:依题意,定滑轮受三个力作用而处于静止,即两段轻绳分别对它产生斜向左上方和竖直向下的拉力
解析:依题意,定滑轮受三个力作用而处于静止,即两段轻绳分别对它产生斜向左上方和竖直向下的拉力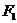 和
和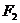 (其大小均为
(其大小均为 ),以及横梁对它产生的弹力
),以及横梁对它产生的弹力 。根据共点力的平衡条件可知,这三个力的合力应该为0,所以
。根据共点力的平衡条件可知,这三个力的合力应该为0,所以 的方向就和拉力
的方向就和拉力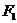 和
和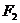 的合力
的合力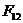 方向相反,如图8所示。
方向相反,如图8所示。
思路点拨:此题容易得出的一个错误结论就是:误认为杆对滑轮的作用力沿杆水平向右。且记:杆对物体的弹力不一定沿杆,要根据物体所处的状态,进行受力分析,从而得出正确的结论。
1.根据物体产生的形变方向进行判断:
⑴弹簧产生的弹力方向:与弹簧的中心轴线重合,指向弹簧形变的反方向,如图1所示。
⑵轻绳类物体产生的弹力方向:沿绳子并指向绳子收缩的方向,如图2所示。
 ⑶“点”和“面”(包括“平面”或“曲面”,下同)接触、“面”与“面”接触时,弹力沿着过接触点、垂直于接触面(或接触面的切面)并指向受力物体,如图3、图4所示。
⑶“点”和“面”(包括“平面”或“曲面”,下同)接触、“面”与“面”接触时,弹力沿着过接触点、垂直于接触面(或接触面的切面)并指向受力物体,如图3、图4所示。
值得注意的是:一定要说清楚是哪一个物体产生的弹力方向,或者说清楚是哪一个物体所受的弹力方向。就像图1中箭头所表示的是弹簧产生的弹力方向(或者是被悬挂物体所受的弹力方向)。
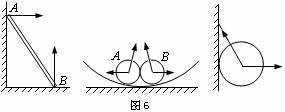
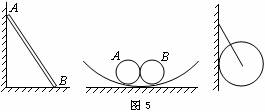 例题1.请在下图5中画出杆或球所受的弹力方向。
例题1.请在下图5中画出杆或球所受的弹力方向。
解析:根据上面的结论,很快画出杆或球所受弹力的方向如图6所示。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com