
8.下列实验说法完全正确的是( )
A配制一定浓度的NaOH溶液:把NaOH放在右盘
B配制一定浓度的HCl溶液:转移时不需要玻璃棒
C测定中和热:环形玻璃棒应上下搅拌
D分离两种互溶的液体:从冷凝器上、下口出水
7.实验室里可用五氧化二磷作为干燥剂来干燥,用排空法收集,多余气体可用水吸收的气体为()A. NH3 B.Cl2 C.CO D.HCl
6. 在氯水中存在多种分子和离子,也可以通过实验的方法加以确定。下列说法错误的是()
A.加入含有NaOH的酚酞试液,红色褪去,说明有H+离子存在
B.加入有色布条后,有色布条褪色,说明有HClO分子存在
C.氯水呈浅黄绿色,且有刺激性气味,说明有C12分子存在
D.加入硝酸酸化的AgNO3溶液产生白色沉淀,说明有Cl-离子存在
2. 老鼠离开洞穴沿直线前进,它的速度与到洞穴的距离成反比,当它行进到离洞穴的距离为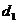 的甲处时速度为
的甲处时速度为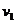 ,试求:⑴老鼠行进到离洞穴的距离为
,试求:⑴老鼠行进到离洞穴的距离为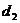 的乙处时速度多大?⑵从甲处到乙处需要多长时间?
的乙处时速度多大?⑵从甲处到乙处需要多长时间?
解析:⑴老鼠行进的速度与它到洞穴的距离成反比,即有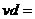 常数
常数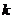 。若设老鼠行进到离洞穴的距离为
。若设老鼠行进到离洞穴的距离为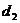 的乙处时速度为
的乙处时速度为 ,则
,则
 常数
常数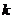
故 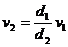
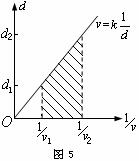 ⑵老鼠的运动速度
⑵老鼠的运动速度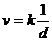 ,如果画它的
,如果画它的 图象,应该是一条双曲线,不利于解决问题。但若是画出
图象,应该是一条双曲线,不利于解决问题。但若是画出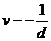 图象,就是一条过原点的倾斜直线(如图5所示)了,对问题的处理就显得简单得多。从图象可以看出,图象与横轴所围面积的单位,即
图象,就是一条过原点的倾斜直线(如图5所示)了,对问题的处理就显得简单得多。从图象可以看出,图象与横轴所围面积的单位,即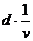 的单位就是时间的单位,所以老鼠从甲处行进到乙处所用的时间等于图中画斜线的梯形面积值,即
的单位就是时间的单位,所以老鼠从甲处行进到乙处所用的时间等于图中画斜线的梯形面积值,即

这其实是一个图象知识的迁移问题,通过思维转换,画出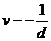 图象,把本来不好解决的问题变得十分简单,这其实也是一个图象的妙用。
图象,把本来不好解决的问题变得十分简单,这其实也是一个图象的妙用。
1. 离地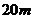 高处有一小球
高处有一小球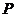 做自由落体运动,此时其正下方地面上有另一小球
做自由落体运动,此时其正下方地面上有另一小球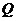 以
以 的初速度竖直上抛,试求:
的初速度竖直上抛,试求:
⑴经多长时间两小球在空中相遇?
⑵若要使两球在空中相遇,球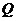 上抛的初速度最小满足什么条件?
上抛的初速度最小满足什么条件?
解析:以小球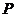 为参照系,则小球
为参照系,则小球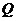 便以
便以 的速度做匀速直线运动。
的速度做匀速直线运动。
⑴设小球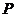 和
和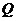 经过时间
经过时间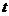 相遇,则
相遇,则

⑵设小球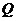 上抛的最小速度为
上抛的最小速度为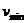 ,则
,则
小球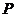 下落到地面所需的时间为
下落到地面所需的时间为

在空中相遇必须满足
 ≤
≤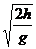
即 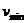 ≥
≥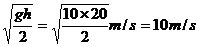
可见,选择小球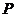 为参照系后,对问题的解决带来了多大的方便。
为参照系后,对问题的解决带来了多大的方便。
4.学会知识的迁移
例题4.在奥运会上,一跳水运动员从离水面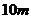 高的平台上向上跃起,举起双臂直立离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高
高的平台上向上跃起,举起双臂直立离开台面,此时其重心位于从手到脚全长的中点,跃起后重心升高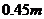 到达最高点,落水时身体直立,手先入水(此过程中运动员水平方向的运动忽略不计),从离开跳台到手触水面,它可用来完成空中动作的时间是多少?(计算时,可以把运动员看作全部质量集中于一点的一个质点,取
到达最高点,落水时身体直立,手先入水(此过程中运动员水平方向的运动忽略不计),从离开跳台到手触水面,它可用来完成空中动作的时间是多少?(计算时,可以把运动员看作全部质量集中于一点的一个质点,取 ,结果保留两位有效数字)
,结果保留两位有效数字)
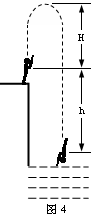 解析:根据题意画出草图如图4所示,运动员从平台跃起到双手接触水面,其重心的高度变化为
解析:根据题意画出草图如图4所示,运动员从平台跃起到双手接触水面,其重心的高度变化为
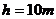
法一:将整个过程分为上升和下降两个阶段考虑,设运动员跃起的初速度为 ,则
,则

故 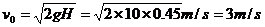
上升的时间为
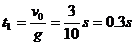
设运动员从最高点到手接触水面的所用的时间为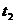 ,则
,则
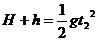
故 
空中完成动作的时间为
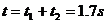
法二:运动员的整个运动过程为竖直上抛运动,设总时间为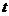 ,由于运动员入水时位于跃起位置下方
,由于运动员入水时位于跃起位置下方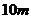 处,故整个过程的位移为
处,故整个过程的位移为

代入数据整理,得
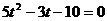
解得 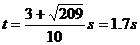 (另一根已舍去)
(另一根已舍去)
点拨:①把实际问题合理取舍,建立物理模型,通过类比,使所学的知识迁移到新的物理情景中去,解决实际问题;②象竖直上抛运动这样,全过程是匀变速直线运动的,分上升和下降阶段讨论虽然易于理解,但不如全过程处理更简便、快捷,只不过此时要注意速度、加速度,特别是位移矢量的方向问题。
[学以致用]
3.谨防温柔的陷阱
例题3.一辆汽车以 的速度行驶,现因故紧急刹车。已知汽车刹车过程中加速度的大小为
的速度行驶,现因故紧急刹车。已知汽车刹车过程中加速度的大小为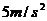 ,则从开始刹车经过
,则从开始刹车经过 ,汽车通过的距离是多少?
,汽车通过的距离是多少?
解析:汽车刹车的过程中作匀减速直线运动,但当汽车停止运动后,加速度就消失,故题中所给的时间内是否汽车一直在做匀减速直线运动,还需要判断。设汽车从刹车到停止运动所用的时间为 ,并选取初速度的方向为正方向,则由速度公式得
,并选取初速度的方向为正方向,则由速度公式得

所以 
可见,汽车刹车后经过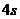 就停止运动,后
就停止运动,后 其实是静止不动的。
其实是静止不动的。
由位移公式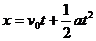 可以求出刹车
可以求出刹车 内通过的位移为
内通过的位移为
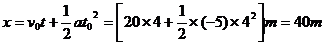
点拨:①此题容易犯如下的错误:直接将 代入位移公式,即
代入位移公式,即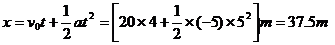 ,乍看这个结果好象符合实际,因为结果不象原来所做的这类问题中结果为负值的情况,不容易引起怀疑,是一个温柔的陷阱。其实把这个结果和上面的答案加以对比,你就会发现
,乍看这个结果好象符合实际,因为结果不象原来所做的这类问题中结果为负值的情况,不容易引起怀疑,是一个温柔的陷阱。其实把这个结果和上面的答案加以对比,你就会发现 实际上就是汽车停止后又反向加速运动
实际上就是汽车停止后又反向加速运动 的总位移,显然与实际情况不符。②此题在做出经过
的总位移,显然与实际情况不符。②此题在做出经过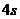 就停止的判断后,也可以用推论公式
就停止的判断后,也可以用推论公式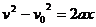 直接求出答案。
直接求出答案。
2.匀变速直线运动问题的求解方法
 例题2.物体以一定的初速度从点
例题2.物体以一定的初速度从点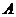 冲上固定的光滑斜面,到达
冲上固定的光滑斜面,到达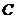 点时的速度恰好减小为0,如图2所示。已知物体运动到
点时的速度恰好减小为0,如图2所示。已知物体运动到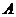 、
、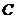 两点间距离的
两点间距离的 处的
处的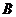 点时,所用的时间为
点时,所用的时间为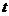 ,试求物体从
,试求物体从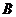 点滑到
点滑到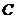 点所用的时间。
点所用的时间。
解法一:逆向思维法
物体向上匀减速冲上斜面,相当于向下匀加速滑下斜面,则
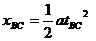

又 
解得 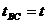
解法二:特殊规律的应用
对于初速度为0的匀加速直线运动,在连续相等时间内通过的位移之比为
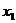 ︰
︰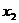 ︰
︰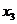 ︰……
︰……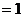 ︰
︰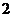 ︰
︰ ︰……
︰……
显然 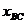 ︰
︰ ︰
︰
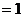 ︰
︰
通过 的时间为
的时间为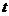 ,故通过
,故通过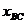 的时间为
的时间为
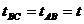
解法三:中间时刻速度法
全段的平均速度为
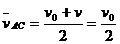
又 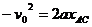 ,
, ,且
,且
解得 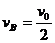
可以看出,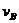 正好等于全段的平均速度
正好等于全段的平均速度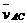 ,因此
,因此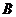 点是全段中间时刻的位置,所以
点是全段中间时刻的位置,所以
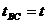
解法四:面积法
 利用相似三角形面积的比等于对应边平方比的方法,作出如图3所示的速度时间图象,则
利用相似三角形面积的比等于对应边平方比的方法,作出如图3所示的速度时间图象,则

且  ,
, ,
,
解得 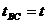
点拨:以上的几种解法,还不包括常规解法,通过对解题方法的挖掘,加强了灵活运用匀变速运动的各种规律推理的能力、逆向思维训练的能力,通过面积法的运用,还加强了灵活运用知识处理物理问题的能力。
1.有关巧选参照系的问题
例题1.轮船在河流中逆流而上,下午7时,船员发现轮船上的一橡皮艇已失落水中,船长马上命令调转船头寻找橡皮艇,经过一个小时的追寻,终于追上了顺流而下的橡皮艇。如果轮船在整个过程中相对于水的速度不变,那么据此判断橡皮艇是在何时失落在水中的?
 解析一:以河岸为参照系,如图1所示,假设橡皮艇在
解析一:以河岸为参照系,如图1所示,假设橡皮艇在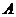 点失落,当轮船航行至
点失落,当轮船航行至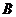 点时才发觉,此时橡皮艇已经随水漂流到
点时才发觉,此时橡皮艇已经随水漂流到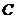 点,轮船调转船头后到
点,轮船调转船头后到 点才追上橡皮艇。从失落起到发现橡皮艇失落经历的时间为
点才追上橡皮艇。从失落起到发现橡皮艇失落经历的时间为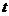 ,则由图中可以看出
,则由图中可以看出

即
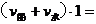
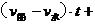



解得 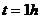
此题若是以流水为参照系,则思路会更简洁:
解析二:以流水为参照系,则橡皮艇相对于流水是静止不动的,而轮船相对于水的速度不变,从失落点到发现点,再从发现点“回到”橡皮艇位置,往返所用的时间是相等的。从发现点经过1个小时追上橡皮艇,那么从失落点到发现点所航行的时间也是一个小时,所以失落的时间就是下午的6时。
点拨:研究物体的运动首先要选取参照系,在一般的问题中都是以地球为参照系。但是在上面的例题中,若是以地球为参照系的话,解题过程将会非常麻烦,这时通过变换参照系的选取,便使得问题的解决大大简化。
(三) .专题预演
专题一:运动学的基本概念
例题1.关于加速度和速度,下列说法中正确的是
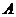 .加速度反映了速度变化的多少
.加速度反映了速度变化的多少
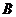 .加速度的方向与速度变化的方向相同
.加速度的方向与速度变化的方向相同
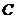 .物体的速度越大,加速度就越大
.物体的速度越大,加速度就越大
 .加速度越大,说明速度变化量越大
.加速度越大,说明速度变化量越大
答案: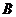
总结:对物理概念,应从以下几个方面加深理解:
①物理概念产生的背景及其描述的意义;
②影响物理概念大小的因素有哪些?
③与其它物理概念的联系和区别;
④在应用的过程中加深对物理概念的理解和巩固。
专题二:匀变速直线运动规律公式的应用
例题2.做匀减速直线运动的物体,经过4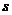 后停止,若在第1
后停止,若在第1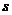 内的位移是14
内的位移是14 ,试求它在最后1
,试求它在最后1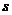 内的位移大小?
内的位移大小?
解析:设运动物体的初速度为 ,加速度大小为
,加速度大小为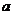 ,1
,1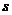 末的速度为
末的速度为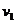 ,3
,3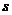 末的速度为
末的速度为 ,运动的总时间为
,运动的总时间为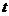 ,则由速度公式得
,则由速度公式得

即 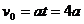
同理  ,
,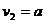
再设第1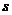 和最后1
和最后1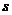 内的位移分别为
内的位移分别为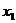 和
和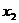 ,再由
,再由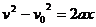 ,得
,得
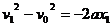 ,
,
代入数据解得

总结:利用匀变速直线运动规律公式解题时,应注意下面的几个问题:
①要快速而准确的找出题目所述的物体的运动过程及初、末状态;
②分析、判断物体的运动性质,有时要画出草图;
③设出正方向,根据题中的已知条件和所求物理量选取合适的公式,列方程求解;
④必要时对结果进行讨论。
专题三:自由落体和竖直上抛运动
例题3.一物体被以 的初速度竖直上抛,试求经过多长时间其离抛出点的高度为
的初速度竖直上抛,试求经过多长时间其离抛出点的高度为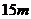 ?取
?取 。
。
解析:因对竖直上抛运动来讲,全过程是一个匀变速运动,故由匀变速运动的位移公式,得
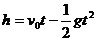
把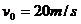 、
、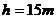 代入上式,得
代入上式,得
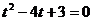
解得
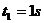 ,
,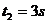
总结:①这其实就是一个匀变速运动中的多解问题,离地面高度为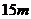 的位置,物体在上升和下降过程中都要经过,所以时间有两个值;
的位置,物体在上升和下降过程中都要经过,所以时间有两个值;
②正方向的匀减速和反方向的匀加速过程合在一起,只要加速度相同,全过程就是一个匀变速运动过程,对这样的运动过程,一般不要分过程考虑,全过程应用匀变速运动规律公式是比较方便的。
专题四:追及和相遇问题
例题4.一辆公共汽车由静止开始以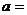
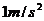 的加速度沿直线前进,车后相距
的加速度沿直线前进,车后相距 处,与车行使方向相同,某人开始以
处,与车行使方向相同,某人开始以 的速度匀速追车,问人能否追上汽车?若能追上,求追上的时间;若追不上,求人、车间的最小距离。
的速度匀速追车,问人能否追上汽车?若能追上,求追上的时间;若追不上,求人、车间的最小距离。
解析:由题意可知,人和车运动的时间相等,设人经过时间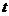 追上汽车,当追上时,人和车的位移关系为
追上汽车,当追上时,人和车的位移关系为

即 
整理得
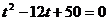
上面的式子有解则能追上,否则追不上。
因 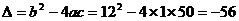 <
<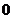 ,
,
故人是追不上汽车的
在人追赶汽车的过程中,当汽车的速度等于人的速度时,人和车之间的距离最小。设从开始追赶到两者距离最小所用时间为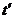 ,则有
,则有
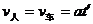
所以
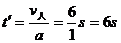
此时人和汽车之间的距离最小为

总结:追及与相遇问题,应从以下面两个方面进行考虑:
①解决这类问题最关键的就是当追及或相遇时,两物体必须在同一位置,则两物体的运动时间、速度和位移就有了确定的关系,要根据各个物体运动的特点,分别列出速度和位移关系式;
②追及物体和被追及物体的速度相等,是此类问题中的重要临界条件。根据不同的题目条件,速度相等往往是两物体相距最远、最近或追上等的临界条件,应根据题目条件具体分析。
专题五:探究匀变速运动的速度随时间的变化
 例题5.在“探究匀变速运动的速度随时间的变化关系”的实验中,某同学在打出的纸带上每5个计时点取一个计数点,共取了7个计数点,测出每两个相邻计数点间的距离分别为
例题5.在“探究匀变速运动的速度随时间的变化关系”的实验中,某同学在打出的纸带上每5个计时点取一个计数点,共取了7个计数点,测出每两个相邻计数点间的距离分别为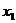 、
、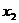 、
、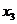 、……
、…… ,然后把它们准确的剪开成6段,按图那样贴在坐标纸上,彼此不留间隙也不重叠,纸带的下端都准确的与横轴重合,第一段纸带
,然后把它们准确的剪开成6段,按图那样贴在坐标纸上,彼此不留间隙也不重叠,纸带的下端都准确的与横轴重合,第一段纸带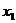 准确的与纵轴重合,横轴为时间轴,纵轴为速度轴。该同学在这个图中利用各段纸带上边沿的中点作出了速度时间如图所示,根据作出的图象是一条倾斜的直线,从而就判断物体所做的是匀变速直线运动,请你说明他判断的依据。
准确的与纵轴重合,横轴为时间轴,纵轴为速度轴。该同学在这个图中利用各段纸带上边沿的中点作出了速度时间如图所示,根据作出的图象是一条倾斜的直线,从而就判断物体所做的是匀变速直线运动,请你说明他判断的依据。
解析:由于各段纸带是等宽的,所以每条纸带的宽度可以表示一个时间单位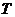 ,每条纸带的高度
,每条纸带的高度 和该单位时间内
和该单位时间内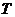 内的平均速度
内的平均速度 的关系为
的关系为
 ,而
,而 等于时间
等于时间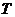 中间时刻的瞬时速度
中间时刻的瞬时速度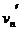 ,即有
,即有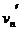 =
=
 ,这样
,这样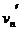 就是第
就是第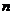 段纸带上边沿中点的速度(当
段纸带上边沿中点的速度(当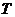 =
= 时,纵轴
时,纵轴 高就表示
高就表示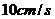 的速度),因此测出各段纸带中点的位置1、2、3、……6,利用这些点便可画出速度时间图象,因为画出的速度时间图象是一条倾斜直线,就证明该物体做的就是匀变速直线运动。(另外,利用图象就可以求出物体运动的加速度了,如利用图中相距较远的
的速度),因此测出各段纸带中点的位置1、2、3、……6,利用这些点便可画出速度时间图象,因为画出的速度时间图象是一条倾斜直线,就证明该物体做的就是匀变速直线运动。(另外,利用图象就可以求出物体运动的加速度了,如利用图中相距较远的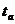 和
和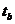 两个时刻所对应的速度
两个时刻所对应的速度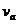 和
和 可以求得加速度)
可以求得加速度)
总结:该题中是如何利用纸带的长度来代替速度的?与常规题相比,这样能使问题作怎样的简化?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com