
(一)认识旧社会的黑暗和不公,学习劳动人民无私的奉献精神。
根据“若a>0,b>0,a>b,n为自然数,则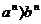 ;反之若a>0,b>0,n为自然数
;反之若a>0,b>0,n为自然数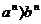 ,则a>b” 来比较两个有理数的大小.
,则a>b” 来比较两个有理数的大小.
例7 比较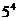 与
与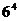 的大小
的大小
解析:因为5与6都是大于0的数,根据“若a>0,b>0,n为自然数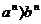 ,则a>b”,于是有
,则a>b”,于是有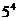 <
<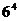 .
.
利用“若 则a<b;若
则a<b;若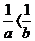 ,则a>b;若
,则a>b;若 ,则a=b.”来比较两个有理数的大小.
,则a=b.”来比较两个有理数的大小.
例6在下列两个数之间填上“ ”或“<”符号.
”或“<”符号.
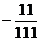
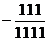
解析:因为 =10+
=10+ ,
, =
=
10+ ,所以
,所以 >
> ,
,
> .于是
.于是
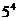 与
与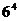
 .
.
故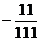 >
> .
.
根据“a、b均为正数,则由 ,
,
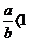 ,得出结论a>b,a=b,a<b.” 来比较两个有理数的大小.
,得出结论a>b,a=b,a<b.” 来比较两个有理数的大小.
例5在下列两个数之间填上“>”或“<”符号.
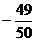

解析:由于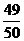
 =
=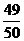

=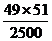 <1,则
<1,则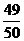
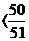 .
.
再根据“两个负数绝对值大的反而小”,
得到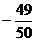
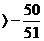 .
.
根据“由a-b>0,则a>b;若a-b=0,则a=b;若a-b<0,a<b.”来比较两个有理数的大小.
例4 在下列两个数之间填上“>”或“<”符号.

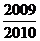
解析:由于
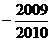
 <0,所以
<0,所以
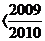 .
.
根据“几个分数,分子(分母)相等,分母(分子)大的反而小(大)”来进行比较.
例3 用“>”连接下列各数:
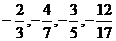
解析:本题若化为同分母的分数相比较,则运算量较大,且复杂烦琐,于是可考虑先将它们化成同分子的分数再比较.
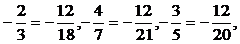 由于
由于 再根据“两个负数绝对值大的反而小”,得到
再根据“两个负数绝对值大的反而小”,得到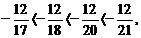 即
即
根据“在数轴上右边的点表示的数总比左边的点表示的数大”可以利用数形结合来比较,这种方法特别适宜用于同时比较多个有理数的大小的情况.
例2 用“<”连接下列各数:
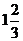 ,-2.5,3,
,-2.5,3,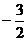 ,0.8,-1,0.
,0.8,-1,0.
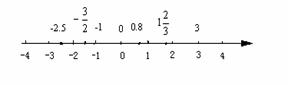 解析:将各数用数轴上的点表示出来,如图所示:
解析:将各数用数轴上的点表示出来,如图所示:
根据“在数轴上右边的点表示的数总比<左边的点表示的数大”,得到-2.5<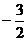 <-1<0<0.8<
<-1<0<0.8<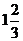 <3.
<3.
根据有理数比较大小的法则“正数大于0,负数都小于0;正数都大于一切负数;两个负数绝对值大的反而小”来进行比较,这是比较有理数大小的最常用的方法.
例1 在冬季的一天我国三个城市的最高气温分别是-10℃、1℃、-7℃,把它们从高到低排列正确的是( )
(A)-10℃、-7℃、1℃
(B)-7℃、-10℃、1℃
(C)1℃、-7℃、-10℃
(D)1℃、-10℃、-7℃
解析:本题目是一道实际问题,题目中的数据经过大小比较,就可以得出结果.根据“正数大于负数”可知,三个量中1℃最大,再根据“两个负数绝对值大的反而小”便可知-7℃>-10℃,于是有把它们从高到低排列为1℃、-7℃、-10℃.故选(C).
20.(I)因 ……………… 2
……………… 2
而函数 在
在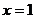 处取得极值2
处取得极值2
所以
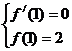
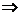

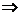
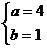
所以
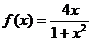 为所求
……………… 4分
为所求
……………… 4分
验证(略) ……………… 6分
(II)由(I)知, 在
在 上为增函数,在
上为增函数,在 上为减函数,
上为减函数,
(1)若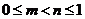 ,则
,则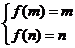 ,无解.……………… 8分
,无解.……………… 8分
(2)若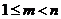 ,则
,则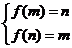 ,无解.……………… 10分
,无解.……………… 10分
(3)若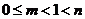 ,则
,则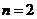 ,而
,而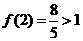 ,所以
,所以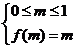 ,解得
,解得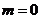 .
.
综合知,满足条件的区间为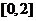 .……………… 12分
.……………… 12分
(Ⅲ)
由条件知,过 的图形上一点
的图形上一点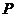 的切线
的切线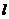 的斜率
的斜率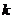 为:
为:
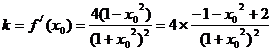
 ………………15分
………………15分
令 ,则
,则 此时 ,
此时 ,
根据二次函数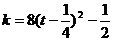 的图象性质知:
的图象性质知:
当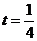 时,
时,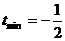 当
当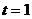 时,
时,
所以,直线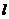 的斜率
的斜率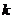 的取值范围是
的取值范围是 . ……………… 18分
. ……………… 18分
20.(18分)已知函数 在
在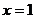 处取得极值
处取得极值 .
.
(I) 求函数 的表达式;
的表达式;
(II)若 的定义域、值域均为
的定义域、值域均为 ,(
,(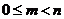 )试求所有满足条件的区间
)试求所有满足条件的区间 ;
;
(Ⅲ)若直线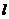 与
与 的图象切于点
的图象切于点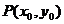 ,求直线
,求直线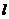 的斜率
的斜率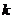 的范围.
的范围.
19解:(1)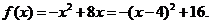
当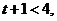 即
即 时,
时, 在
在 上单调递增,
上单调递增, 
当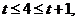 即
即 时,
时,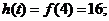
当 时,
时, 在
在 上单调递减,
上单调递减, 
综上,
(2)函数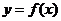 的图象与
的图象与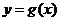 的图象有且只有三个不同的交点,即函数
的图象有且只有三个不同的交点,即函数
 的图象与
的图象与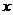 轴的正半轴有且只有三个不同的交点。
轴的正半轴有且只有三个不同的交点。
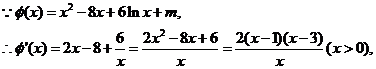
当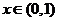 时,
时,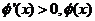 是增函数;当
是增函数;当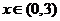 时,
时,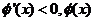 是减函数;
是减函数;
当 时,
时,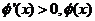 是增函数;当
是增函数;当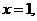 或
或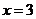 时,
时,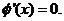

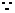 当
当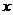 充分接近0时,
充分接近0时,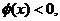 当
当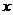 充分大时,
充分大时,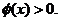
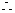 要使
要使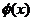 的图象与
的图象与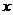 轴正半轴有三个不同的交点,必须且只须
轴正半轴有三个不同的交点,必须且只须
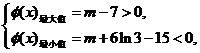 即
即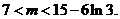 所以存在实数
所以存在实数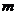 ,使得函数
,使得函数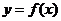 与
与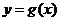 的图象有且只有三个不同的交点,
的图象有且只有三个不同的交点,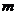
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com