
6.设 的图象可能是 ( )
的图象可能是 ( )

5.为得到函数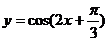 的图象,只需将函数
的图象,只需将函数 的图象 ( )
的图象 ( )
A.向左平移 个长度单位 B.向右平移
个长度单位 B.向右平移 个长度单位
个长度单位
C.向左平移 个长度单位 D.向右平移
个长度单位 D.向右平移 个长度单位
个长度单位
4.在二项式 的项的系数是 ( )
的项的系数是 ( )
A.-10 B.10 C.-5 D.5
3.已知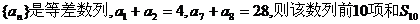 等于 ( )
等于 ( )
A.64 B.100 C.110 D.120
2.定义集合运算: 的所有元素之和为 ( )
的所有元素之和为 ( )
A.0 B.2 C.3 D.6
1.复数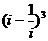 等于 ( )
等于 ( )
A.8 B.-8 C.8i D.-8i
21.解:(1)由题意 即
即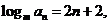
∴ ………………2分
………………2分
∴ ∵m>0且
∵m>0且 ,∴m2为非零常数,
,∴m2为非零常数,
∴数列{an}是以m4为首项,m2为公比的等比数列 …………4分
(2)由题意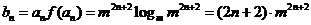 ,
,
当
∴ ①
…………6分
①
…………6分
①式乘以2,得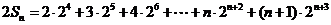 ② …7分
② …7分
②-①并整理,得

=

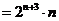 ………… 10分
………… 10分
(3)由题意 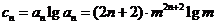 ,要使
,要使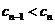 对一切
对一切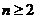 成立,
成立,
即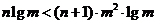 对一切
对一切 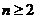 成立,
成立,
①当m>1时, 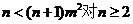 成立;
…………12分
成立;
…………12分
②当0<m<1时,
∴ 对一切
对一切 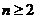 成立,只需
成立,只需 ,
,
解得  , 考虑到0<m<1, ∴0<m<
, 考虑到0<m<1, ∴0<m<
综上,当0<m< 或m>1时,数列
或m>1时,数列 中每一项恒小于它后面的项…………14分
中每一项恒小于它后面的项…………14分
20.解析:(1)依题意,圆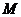 的半径等于圆心
的半径等于圆心 到直线
到直线 的距离,
的距离,
即 .
…………………4分
.
…………………4分
∴圆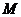 的方程为
的方程为 . …………………6分
. …………………6分
(2)设 ,由
,由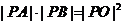 ,
,
得 ,
,
即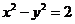 .
……………………………………9分
.
……………………………………9分
 ……11分
……11分
∵点在圆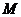 内,∴
内,∴ ,
,
∴的取值范围为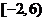 . ……………………………………………14分
. ……………………………………………14分
18.(本小题满分14分)
解:(1)证明:连结 ,则
,则 是
是 的中点,
的中点,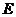 为
为 的中点
的中点
故在△ 中,
中, 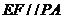 ,
…………3分
,
…………3分
且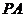
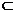 平面PAD,
平面PAD,
 平面PAD,∴
平面PAD,∴ ∥平面PAD …………6分
∥平面PAD …………6分
(2)取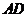 的中点M,连结
的中点M,连结 ,
, ,
,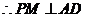 …………8分
…………8分
又平面 ⊥平面
⊥平面 , 平面
, 平面 ∩平面
∩平面 =
=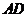 ,
,
 ,
……………10分
,
……………10分
 ……………14分
……………14分
19解:(1)设切线的斜率为k,则 ………2分
………2分
又 ,所以所求切线的方程为:
,所以所求切线的方程为: …………5分
…………5分
即 …………6分
…………6分
(2) , 要使
, 要使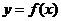 为单调增函数,必须满足
为单调增函数,必须满足
即对任意的 …………8分
…………8分
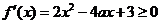
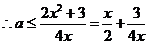 …………11分
…………11分
而 ,当且仅当
,当且仅当 时,等号成立, 所以
时,等号成立, 所以
所求满足条件的a 值为1 …………………………………14分
17.(本小题满分12分)
解:(1) 共有
共有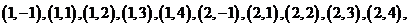
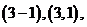
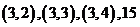 种情况
…………4分
种情况
…………4分
函数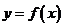 有零点,
有零点, ,有
,有 共6种情况满足条件
………6分
共6种情况满足条件
………6分
所以函数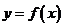 有零点的概率为
有零点的概率为 ………8分
………8分
(2)函数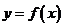 的对称轴为
的对称轴为 在区间
在区间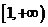 上是增函数则有
上是增函数则有 ,
, 
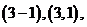
 共13种情况满足条件
……10分
共13种情况满足条件
……10分
所以函数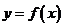 在区间
在区间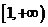 上是增函数的概率为
上是增函数的概率为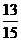 ………12分
………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com