
5.设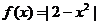 ,若
,若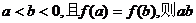 的取值范围是
的取值范围是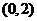 .
.
4.关于函数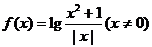 ,有下列命题:①其图象关于
,有下列命题:①其图象关于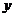 轴对称;②当
轴对称;②当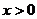 时,
时,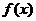 是增函数;当
是增函数;当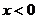 时,
时,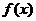 是减函数;③
是减函数;③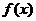 的最小值是
的最小值是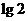 ;④
;④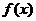 在区间
在区间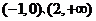 上是增函数;⑤
上是增函数;⑤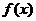 无最大值,也无最小值.
无最大值,也无最小值.
其中所有正确的个数是 3 .
3.设函数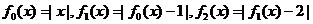 ,则函数
,则函数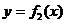 的图象与
的图象与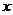 轴所围成的图形中封闭部分的面积为
7 .
轴所围成的图形中封闭部分的面积为
7 .
2.将函数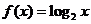 的图象绕原点
的图象绕原点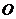 逆时针旋转
逆时针旋转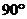 得到函数
得到函数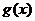 的图象,则
的图象,则 = 4 .
= 4 .
1.二次函数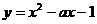 在区间
在区间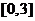 上有最小值
上有最小值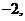 则实数
则实数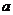 的值为
2 .
的值为
2 .
14.已知t为常数,函数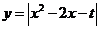 在区间[0,3]上的最大值为2,则t=_1_.
在区间[0,3]上的最大值为2,则t=_1_.
13..对于在区间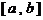 上有意义的两个函数
上有意义的两个函数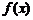 和
和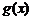 ,如果对任意
,如果对任意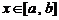 ,均有
,均有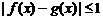 , 那么我们称
, 那么我们称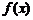 和
和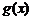 在
在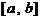 上是接近的.若
上是接近的.若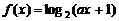 与
与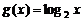 在闭区间
在闭区间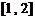 上是接近的,则的取值范围是
上是接近的,则的取值范围是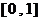 .
.
12.已知二次函数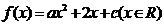 的值域为
的值域为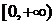 ,则
,则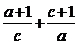 的最小值为4.
的最小值为4.
11.若关于 的不等式
的不等式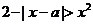 至少有一个负数解,则实数
至少有一个负数解,则实数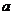 的取值范围是
的取值范围是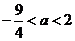 .
.
10.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂价就降低0.02元,但实际出厂价不能低于51元.
(1)当一次订购量为550 个时,零件的实际出厂价恰降为51元?
(2)设一次订购为 个,零件的实际出厂单价为
个,零件的实际出厂单价为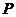 元,函数
元,函数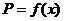 =
=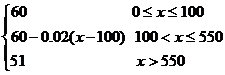 ;
;
(3)当销售量一次订购500个零件时,该厂获得的利润是6000元;如果订购1000个,利润又是1100元.(工厂售出一个零件的利润=实际出厂单价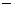 成本)
成本)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com