17．一场晚会有5个唱歌节目和3个舞蹈节目，要求排出一个节目单

　 (1)前4个节目中要有舞蹈，有多少种排法？

　　 (2) 3个舞蹈节目要排在一起，有多少种排法？

　　 (3) 3个舞蹈节目彼此要隔开，有多少种排法？

16．(1)有5本不同的书，从中选3本送给3名同学，每人各一本，共有　　 种

不同的送法；

　　 (2)有5种不同的书，要买3本送给3名同学，每人各一本，共有　　 种不同的送法．

15．将红、黄、蓝、白、黑5种颜色的小球，分别放入红、黄、蓝、白、黑5种颜色的口袋中，但红口袋不能装入红球，则有　　　　　　 种不同的放法．

14．五男二女排成一排，若男生甲必须排在排头或排尾，二女必须排在一起，不同的排法共有　　　　　　　　 种．

13．6个人站一排，甲不在排头，乙不在排尾，共有　　　　 种不同排法．

12．6个人站一排，甲不在排头，共有　　　　　 种不同排法．

22．(14分)

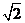设椭圆E: (a,b>0)过M(2，) ，N(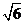,1)两点，O为坐标原点．

　 (Ⅰ)求椭圆E的方程；

　 (Ⅱ)是否存在圆心在原点的圆，使得该圆的任意一条切线与椭圆E恒有两个交点A,B,

　　　　 且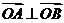？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理

21．(12分)如图，已知椭圆的中心在原点，焦点在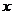轴上，长轴长是短轴长的2倍且经过点M(2,1)，平行于OM的直线l在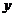轴上的截距为，l交椭圆于A、B两个不同点．

　 (1)求椭圆的方程；

　 (2)求m的取值范围；

　 (3)求证直线MA、MB与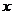轴始终围成一个等腰三角形．

20．(12分)

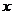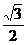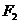已知椭圆G的中心在坐标原点,长轴在轴上,离心率为,两个焦点分别为和,椭

圆G上一点到和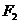的距离之和为12．圆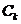: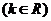的圆心为点．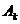

　 (1)求椭圆G的方程

　 (2)求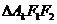的面积

　 (3)问是否存在圆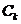包围椭圆G?请说明理由．

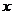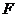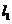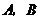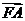19．(12分)双曲线的中心为原点，焦点在轴上，两条渐近线分别为，经过右焦点垂直于的直线分别交于两点．已知成等差数列，且与同向．

　 (Ⅰ)求双曲线的离心率；

　 (Ⅱ)设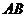被双曲线所截得的线段的长为4，求双曲线的方程．