
第一节:单项选择 (共15小题;每小题1分,满分15分)
从A、B、C、D四个选项中,选出可以填入空白处的最佳选项,并在答题卡上将该项涂黑。
21. At the end of the cross-talk, __ audience present in the hall burst into ___ laughter.
A. an ; the B. the ; a C. an ; / D. the; /
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
创设情境提出问题 |
思考:实数有相关系,大小关系,类比实数之间的关系,联想集合之间是否具备类似的关系. |
师:对两个数a、b,应有a>b或a = b或a<b. 而对于两个集合A、B它们也存在A包含B,或B包含A,或A与B相等的关系. |
类比生疑, 引入课题 |
|
概念形成 |
分析示例: 示例1:考察下列三组集合,并说明两集合内存在怎样的关系  (1)A = {1,2,3}  B = {1,2,3,4,5}  (2)A = {新华中学高(一)6班的全体女生}  B = {新华中学高(一)6 班的全体学生}  (3)C = {x | x是两条边相等的三角形}  D = {x | x是等腰三角形}  1.子集:  一般地,对于两个集合A、B,如果A中任意一个元素都是B的元素,称集合A是集合B的子集,记作 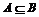 ,读作:“A含于B”(或B包含A) ,读作:“A含于B”(或B包含A) 2.集合相等:  若 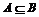 ,且 ,且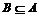 ,则A=B. ,则A=B. |
生:实例(1)、(2)的共同特点是A的每一个元素都是B的元素. 师:具备(1)、(2)的两个集合之间关系的称A是B的子集,那么A是B的子集怎样定义呢?  学生合作:讨论归纳子集的共性.  生:C是D的子集,同时D是C的子集.  师:类似(3)的两个集合称为相等集合.  师生合作得出子集、相等两概念的数学定义. |
通过实例的共性探究、感知子集、相等概念,通过归纳共性,形成子集、相等的概念. 初步了解子集、相等两个概念. |
概念 深化 深化 |
示例1:考察下列各组集合,并指明两集合的关系: (1)A = Z,B = N;  (2)A = {长方形},B = {平行四边形};  (3)A={x| x2–3x+2=0},B ={1,2}.  1.Venn图  用平面上封闭曲线的内部代表集合.  如果 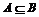 ,则Venn图表示为: ,则Venn图表示为: 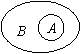   2.真子集  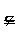 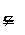 如果集合 如果集合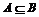 ,但存在元素x∈B,且x ,但存在元素x∈B,且x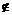 A,称A是B的真子集,记作A A,称A是B的真子集,记作A  B (或B A).  示例3 考察下列集合. 并指出集合中的元素是什么?  (1)A = {(x,y) | x + y =2}.  (2)B = {x | x2 + 1 = 0,x∈R}.  3.空集 称不含任何元素的集合为空集,记作 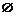 . .规定:空集是任何集合的子集;空集是任何非空集合的真子集. |
示例1
学生思考并回答. 生:(1) 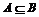 (2) 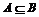 (3)A = B 师:进一步考察(1)、(2) 不难发现:A的任意元素都在B中,而B中存在元素不在A中,具有这种关系时,称A是B的真子集. 示例3 学生思考并回答. 生:(1)直线x+y=2上的所有点 (2)没有元素 师:对于类似(2)的集合称这样的集合为空集. 师生合作归纳空集的定义. |
再次感知子集相等关系,加深对概念的理解,并利用韦恩图从“形”的角度理解包含关系,层层递进形成真子集、空集的概念. |
|
能力 提升 |
一般结论: ① 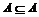 . .②若 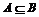 , ,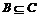 ,则 ,则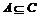 . .③A = B 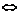 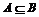 ,且 ,且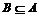 . . |
师:若a≤a,类比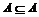 . .若a≤b,b≤c,则a≤c类比. 若 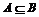 , ,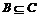 ,则 ,则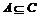 . .师生合作完成: (1)对于集合A,显然A中的任何元素都在A中,故 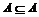 . .(2)已知集合 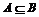 ,同时 ,同时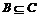 ,即任意x∈A ,即任意x∈A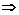 x∈B x∈B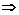 x∈C,故 x∈C,故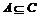 . . |
升华并体会类比数学思想的意义. |
|
应用 举例 |
例1(1)写出集合{a、b}的所有子集; (2)写出集合{a、b、c}的所有子集; (3)写出集合{a、b、c、d}的所有子集; 一般地:集合A含有n个元素 则A的子集共有2n个. A的真子集共有2n – 1个. |
学习练习求解,老师点评总结. 师:根据问题(1)、(2)、(3),子集个数的探究,提出问题: 已知A = {a1,a2,a3…an},求A的子集共有多少个? |
通过练习加深对子集、真子集概念的理解. 培养学生归纳能力. |
|
归纳 总结 |
 子集: 子集: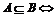 任意x∈A 任意x∈A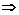 x∈B x∈B真子集:A B 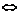 任意x∈A 任意x∈A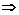 x∈B,但存在x0∈B,且x0 x∈B,但存在x0∈B,且x0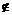 A. A.集合相等:A = B 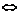 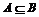 且 且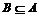 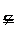 空集( 空集(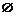 ):不含任何元素的集合 ):不含任何元素的集合性质:① 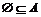 ,若A非空,则 ,若A非空,则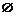 A.
A.② 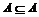 . .③ 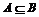 , ,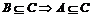 . . |
师生合作共同归纳-总结-交流-完善. 师:请同学合作交流整理本节知识体系 |
引导学生整理知识,体会知识的生成,发展、完善的过程. |
|
课后 作业 |
1.1 第二课时习案 |
学生独立完成 |
巩固基础 提升能力 |
备选训练题
例1
能满足关系{a,b}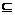 {a,b,c,d,e}的集合的数目是( A )
{a,b,c,d,e}的集合的数目是( A )
A.8个 B.6个 C.4个 D.3个
[解析]由关系式知集合A中必须含有元素a,b,且为{a,b,c,d,e}的子集,所以A中元素就是在a,b元素基础上,把{c,d,e}的子集中元素加上即可,故A = {a,b},A = {a,b,c},A = {a,b,d},A = {a,b,e},A = {a,b,c,d},A = {a,b,c,e},A = {a,b,d,e},A = {a,b,c,d,e},共8个,故应选A.
例2
已知A = {0,1}且B = {x
|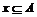 },求B.
},求B.
[解析]集合A的子集共有4个,它们分别是: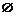 ,{0},{1},{0,1}.
,{0},{1},{0,1}.
由题意可知B = {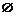 ,{0},{1},{0,1}}.
,{0},{1},{0,1}}.
例3 设集合A = {x – y,x + y,xy},B = {x2 + y2,x2 – y2,0},且A = B,求实数x和y的值及集合A、B.
[解析]∵A = B,0∈B,∴0∈A.
若x + y = 0或x – y = 0,则x2 – y2 = 0,这样集合B = {x2 + y2,0,0},根据集合元素的互异性知:x + y≠0,x – y≠0.
∴ (I) 或
(I) 或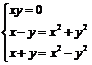 (II)
(II)
由(I)得: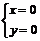 或
或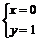 或
或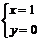
由(II)得: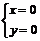 或
或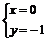 或
或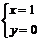
∴当x = 0,y = 0时,x – y = 0,故舍去.
当x = 1,y = 0时,x – y = x + y = 1,故也舍去.
∴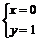 或
或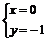 ,
,
∴A = B = {0,1,–1}.
例4
设A = {x | x2
– 8x + 15 = 0},B = {x | ax – 1 = 0},若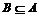 ,求实数a组成的集合,并写出它的所有非空真子集.
,求实数a组成的集合,并写出它的所有非空真子集.
[解析]A = {3,5},∵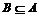 ,所以
,所以
(1)若B =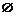 ,则a = 0;
,则a = 0;
(2)若B≠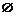 ,则a≠0,这时有
,则a≠0,这时有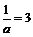 或
或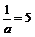 ,即a =
,即a =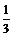 或a =
或a =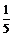 .
.
综上所述,由实数a组成的集合为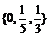 .
.
其所有的非空真子集为:{0},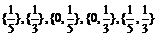 共6个.
共6个.
在从实践到理论,从具体到抽象,从特殊到一般的原则下,一方面注意利用生活实例,引入集合的包含关系. 从而形成子集、真子集、相等集合等概念. 另一方面注意几何直观的应用,即Venn图形象直观地表示、理解集合的包含关系,子集、真子集、集合相等概念及有关性质.
重点:子集的概念;难点:元素与子集,即属于与包含之间的区别.
3.情感、态度与价值观
应用类比思想,在探究两个集合的包含和相等关系的过程中,培养学习的辨证思想,提高学生用数学的思维方式去认识世界,尝试解决问题的能力.
2.过程与方法
(1)通过类比两个实数之间的大小关系,探究两个集合之间的关系.
(2)通过实例分析,获知两个集合间的包含与相等关系,然后给出定义.
(3)从自然语言,符号语言,图形语言三个方面理解包含关系及相关的概念.
1.知识与技能
(1)理解集合的包含和相等的关系.
(2)了解使用Venn图表示集合及其关系.
(3)掌握包含和相等的有关术语、符号,并会使用它们表达集合之间的关系.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com