
5.小明准备参加校运会的跳远比赛,下面是他近期六次跳远的成绩(单位:m):3.6,3.8,4.2,4.0,3.8,4.0.那么,下列结论正确的是
(A)众数是3 .9 m (B)中位数是3.8 m (C)平均数是4.0m (D)极差是0.6m
4.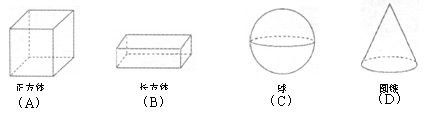 在下面的四个几何体中,左视图与主视图不相同的几何体是
在下面的四个几何体中,左视图与主视图不相同的几何体是
3.据统计,2010年贵阳市参加初中毕业生学业考试的人数约为51000人,将数据51000用科学记数法表示为
(A)5.1×10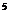 (B)0.51×10
(B)0.51×10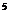 (C)5.1×10
(C)5.1×10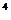 (D)51×10
(D)51×10
2.下列多项式中,能用公式法分解因式的是
(A)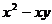 (B)
(B)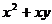 (C)
(C)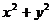 (D)
(D)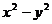
1.-5的绝对值是
(A)5 (B)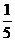 (C) -5 (D) 0.5
(C) -5 (D) 0.5
22.由曲线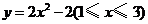 及直线
及直线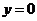 ,绕
,绕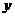 轴旋转所得的旋转体做容器,每秒钟向容器里注水
轴旋转所得的旋转体做容器,每秒钟向容器里注水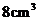 ,问几秒钟后能注满容器?(坐标的长度单位是cm)
,问几秒钟后能注满容器?(坐标的长度单位是cm)
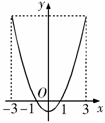 解:如图,底面是
解:如图,底面是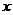 轴上
轴上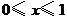 部分的线段绕
部分的线段绕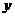 轴旋转所生成的圆,侧面是抛物线
轴旋转所生成的圆,侧面是抛物线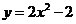 上
上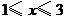 ,
,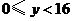 部分绕
部分绕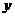 轴旋转所得的曲面.
轴旋转所得的曲面.
由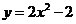 ,得
,得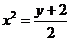 ,
,
注满容器时的体积为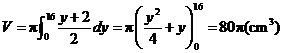 .
.
每秒注水8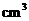 ,充满容器所需时间为
,充满容器所需时间为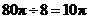 (秒).
(秒).
所以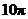 秒钟后能注满容器.
秒钟后能注满容器.
21.甲方是一农场,乙方是一工厂.由于乙方生产须占用甲方的资源,因此甲方有权向乙方索赔以弥补经济损失并获得一定净收入,在乙方不赔付甲方的情况下,乙方的年利润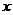 (元)与年产量
(元)与年产量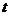 (吨)满足函数关系
(吨)满足函数关系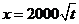 .若乙方每生产一吨产品必须赔付甲方
.若乙方每生产一吨产品必须赔付甲方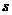 元(以下称
元(以下称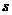 为赔付价格).
为赔付价格).
(1)将乙方的年利润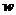 (元)表示为年产量
(元)表示为年产量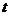 (吨)的函数,并求出乙方获得最大利润的年产量;
(吨)的函数,并求出乙方获得最大利润的年产量;
(2)甲方每年受乙生产影响的经济损失金额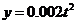 (元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格
(元),在乙方按照获得最大利润的产量进行生产的前提下,甲方要在索赔中获得最大净收入,应向乙方要求的赔付价格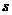 是多少?
是多少?
解:(1)因为赔付价格为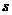 元/吨,所以乙方的实际年利润为
元/吨,所以乙方的实际年利润为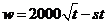 .
.
由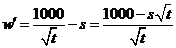 ,
,
令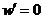 ,得
,得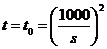 .
.
当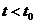 时,
时,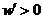 ;当
;当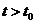 时,
时,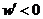 ,
,
所以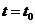 时,
时,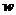 取得最大值.
取得最大值.
因此乙方取得最大年利润的年产量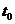 为
为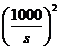 (吨);
(吨);
(2)设甲方净收入为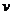 元,则
元,则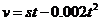 .
.
将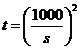 代入上式,得到甲方净收入
代入上式,得到甲方净收入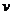 与赔付价格
与赔付价格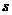 之间的函数关系式
之间的函数关系式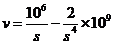 .
.
又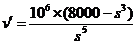 ,
,
令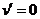 ,得
,得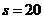 .
.
当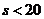 时,
时,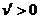 ;当
;当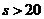 时,
时,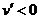 ,
,
所以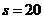 时,
时,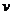 取得最大值.
取得最大值.
因此甲方应向乙方要求赔付价格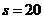 (元/吨)时,获最大净收入.
(元/吨)时,获最大净收入.
20.如图所示,求抛物线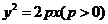 和过它上面的点
和过它上面的点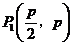 的切线的垂线所围成的平面图形的面积.
的切线的垂线所围成的平面图形的面积.
解:由题意令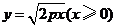 ,
,
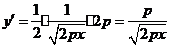 ,
,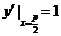 ,
,
所以过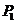 点且垂直于过
点且垂直于过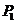 点的抛物线的切线的直线的斜率为
点的抛物线的切线的直线的斜率为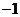 .
.
其方程为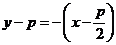 .
.
即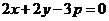 .
.
与抛物线方程联立消去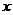 ,得
,得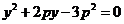 ,
,
解得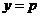 或
或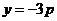 .
.
又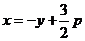 ,所以所求平面图形的面积为
,所以所求平面图形的面积为
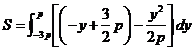
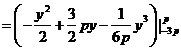
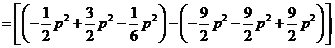
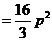 .
.
19.已知函数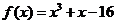 .
.
(1)求曲线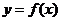 在点
在点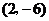 处的切线方程;
处的切线方程;
(2)直线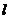 为曲线
为曲线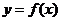 的切线,且经过原点,求直线
的切线,且经过原点,求直线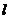 的方程及切点坐标.
的方程及切点坐标.
解:(1)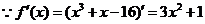 ,
,
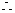 在点
在点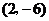 处的切线的斜率
处的切线的斜率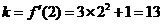 ,
,
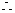 切线的方程为
切线的方程为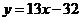 ;
;
(2)设切点为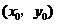 ,则直线
,则直线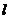 的斜率为
的斜率为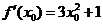 ,
,
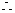 直线
直线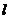 的方程为
的方程为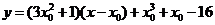 .
.
又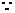 直线
直线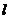 过点
过点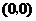 ,
,
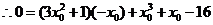 ,
,
整理,得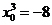 ,
,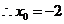 ,
,
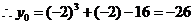 ,
,
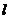 的斜率
的斜率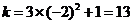 ,
,
 直线
直线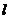 的方程为
的方程为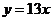 ,切点坐标为
,切点坐标为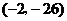 .
.
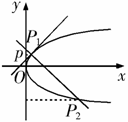
18.已知函数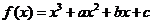 .
.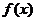 在点
在点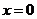 处取得极值,并且在单调区间
处取得极值,并且在单调区间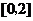 和
和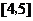 上具有相反的单调性.
上具有相反的单调性.
(1)求实数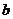 的值;
的值;
(2)求实数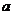 的取值范围.
的取值范围.
解:(1)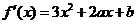 ,因为
,因为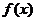 在点
在点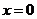 处取得极值,
处取得极值,
所以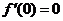 ,即得
,即得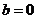 ;
;
(2)令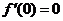 ,即
,即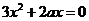 ,
,
解得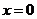 或
或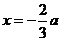 .
.
依题意有 .
.
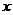 |
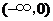 |
0 |
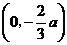 |
 |
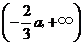 |
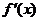 |
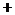 |
0 |
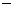 |
0 |
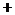 |
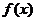 |
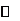 |
极大值 |
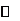 |
极小值 |
 |
因为在函数在单调区间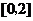 和
和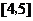 上具有相反的单调性,所以应有
上具有相反的单调性,所以应有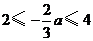 ,
,
解得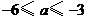 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com