
4.下列各句表意明确,简洁流畅的一句是
A.那位戴博士帽,留短胡须的男老师就是我们的学生科长。
B.在新的形势下,要求我们人人都要学好外语和计算机,只有这样才能适应入世后社会的发展。
C.可怜的阿富汗人民,在遭到残酷的军事打击后又遭受自然灾害--地震,真是祸不单行。
D.我们伟大祖国再也不是一个四分五裂的、任意帝国主义列强侮辱、蹂躏和掠夺的国家了。
3.下面四句中符合语言简明要求的一项是
A.他喜爱冬泳、登山,要把自己锻炼成具有强健体魄的人。
B.进了学校,我们看到同学们正在进行学习,老师们正在进行认真的备课。
C.老师们反复多次地苦口婆心地教导过我们要努力学习。
D.他对我的帮助真是太大了,我真是从内心由衷地感激他。
2.为了使语言简洁流畅,下段文字中,加点的虚词有些应该去掉。根据上下文,应去掉的最恰当的一项是
大约我们的生死不但久已被人随意处置,而且无足轻重,所以自己也看得随随便便,不像欧洲人那样的认真。
A.删去“不但”“所以” B.删去“不但”“而且”“所以”
C.删去“而且”“所以” D.删去“不但”“而且”
1.下列句中加横线的部分都有两个意思,放在句中后,有一处歧义消失了,这一句是
A.天色渐晚,自行车还没修好,修车的急坏了。
B.小刚和小花的爸爸到学校来了。
C.张师傅看到徒弟非常高兴,把他们拉到车间去了。
D.尊敬老师的学生,会得到人们的好评。
22. 解:(I)由图一可得市场售价与时间的函数关系为

由图二可得种植成本与时间的函数关系为
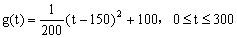
(II)设t时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t),即

当0≤t≤200时,配方整理得

所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得

所以,当t=300时,h(t)取得区间[200,300]上的最大值87.5。
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大。
21.解:当a=0时,函数为f (x)=2x -3,其零点x=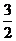 不在区间[-1,1]上。
不在区间[-1,1]上。
当a≠0时,函数f (x) 在区间[-1,1]分为两种情况:
①函数在区间[─1,1]上只有一个零点,此时
 或
或 或
或 或
或 
解得1≤a<5或a=
②函数在区间[─1,1]上有两个零点,此时
 解得a
解得a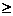 5或a<
5或a<
综上所述,如果函数在区间[─1,1]上有零点,那么实数a的取值范围为(-∞,  ]∪[1, +∞)
]∪[1, +∞)
(别解: ,题意转化为知
,题意转化为知 求
求 的值域,
的值域,
令 得
得 ,
, ,转化为求该函数的值域问题.
,转化为求该函数的值域问题.
20. 解:(1)当 时,
时, ,
,
对任意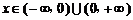 ,
, ,
,
 为偶函数.
为偶函数.
当 时,
时, ,
,
取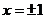 ,得
,得
 ,
,  ,
,
 函数
函数 既不是奇函数,也不是偶函数.
既不是奇函数,也不是偶函数.
(2)解法一:设 ,
,

 ,
,
要使函数 在
在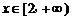 上为增函数,必须
上为增函数,必须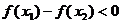 恒成立.
恒成立.
 ,即
,即 恒成立.
恒成立.
又 ,
, .
.
 的取值范围是
的取值范围是 .
.
解法二:当 时,
时, ,显然在
,显然在 为增函数.
为增函数.
当 时,反比例函数
时,反比例函数 在
在 为增函数,
为增函数,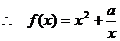 在
在 为增函数.
为增函数.
当 时,同解法一.
时,同解法一.
19.解:(Ⅰ)因为 是奇函数,所以
是奇函数,所以 =0,即
=0,即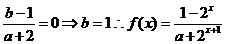
又由f(1)= -f(-1)知
(Ⅱ)解法一:由(Ⅰ)知 ,易知
,易知 在
在 上
上
为减函数。又因 是奇函数,从而不等式:
是奇函数,从而不等式: 
等价于 ,
,
因 为减函数,由上式推得:
为减函数,由上式推得: .即对一切
.即对一切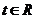 有:
有: ,
,
从而判别式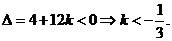
解法二:由(Ⅰ)知 .又由题设条件得:
.又由题设条件得: ,
,
即: ,
,
整理得 

上式对一切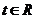 均成立,从而判别式
均成立,从而判别式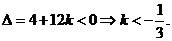
13.-1; 14. ; 15.
; 15.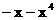 ; 16.
; 16. 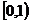 ; 17.(1,4); 18.1,2;
; 17.(1,4); 18.1,2;
3.函数的性质
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com