
18.(满分12分)
某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:K^S*5U.C#O%
|
日 期 |
12月1日 |
12月2日 |
12月3日 |
12月4日 |
12月5日 |
温差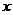 (°C) (°C) |
10 |
11 |
13 |
12 |
8 |
发芽数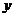 (颗) (颗) |
23 |
25 |
30 |
26 |
16 |
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验
(Ⅰ)求选取的2组数据恰好是不相邻2天数据的概率;
(Ⅱ)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程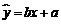 ;K^S*5U.C#O%
;K^S*5U.C#O%
(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
17.(满分12分)
|
分组 |
频数 |
频率 |
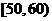 |
4 |
0.08 |
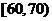 |
③ |
0.16 |
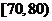 |
10 |
② |
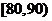 |
16 |
0.32 |
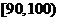 |
|
0.24 |
|
合计 |
① |
|
某中学为增强学生环保意识,举行了“环抱知识竞
赛”,共有900名学生参加这次竞赛为了解本次竞赛
成绩情况,从中抽取了部分学生的成绩(得分均为整
数,满分为100分)进行统计,请你根据尚未完成的频
率分布表解答下列问题:
(Ⅰ)求①、②、③处的数值;
(Ⅱ)成绩在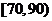 分的学生约为多少人?
分的学生约为多少人?
(Ⅲ)估计总体平均数;
16.某单位为了了解用电量y度与气温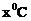 之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:
|
气温(0C) |
18 |
13 |
10 |
-1 |
|
用电量(度) |
24 |
34 |
38 |
64 |
预测当气温为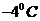 时,用电量的度数约为________.
时,用电量的度数约为________.
15.分别在区间[1,6]和[2,4]内任取一实数,依次记为m和n,则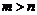 的概率为 ;
的概率为 ;
14.某林场有树苗30000棵,其中松树苗4000棵.为调查树苗的生长情况,采用分层抽样的方法抽取一个容量为150的样本,则样本中松树苗的数量为 ;
|
分数 |
5 |
4 |
3 |
2 |
1 |
|
人数 |
20 |
10 |
30 |
30 |
10 |
13.从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为 ;
12.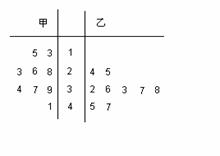 右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图.根据茎叶图,对甲、乙两人这几场比赛得分作比较,得出正确的统计结论是( )
右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图.根据茎叶图,对甲、乙两人这几场比赛得分作比较,得出正确的统计结论是( )
A.甲平均得分比乙高,且甲的得分比乙稳定;
B.乙平均得分比甲高,且乙的得分比甲稳定;
C.甲平均得分比乙低,但甲的得分比乙稳定;
D.乙平均得分比甲低,但乙的得分比甲稳定;
11. 如图,半径为10 cm的圆形纸板内有一个相同圆心的半径为1 cm的小圆.现将半径为1 cm的一枚硬币抛到此纸板上,使硬币整体随机落在纸板内,则硬币落下后与小圆无公共点的概率为( )
如图,半径为10 cm的圆形纸板内有一个相同圆心的半径为1 cm的小圆.现将半径为1 cm的一枚硬币抛到此纸板上,使硬币整体随机落在纸板内,则硬币落下后与小圆无公共点的概率为( )
A.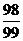 B.
B.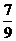 C.
C.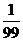 D.
D.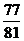
10.为研究变量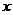 和
和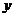 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程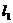 和
和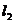 ,两人计算知
,两人计算知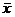 相同,
相同, 也相同,下列正确的是( )
也相同,下列正确的是( )
A.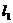 与
与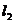 重合
B.
重合
B.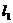 与
与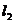 一定平行
一定平行
C.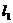 与
与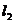 相交于点
相交于点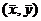 D.无法判断
D.无法判断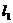 和
和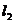 是否相交
是否相交
9.连掷两次骰子得到点数分别为m和n,记向量 的夹角为
的夹角为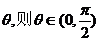 的概率是( )
的概率是( )
A.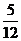 B.
B.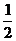 C.
C.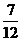 D.
D.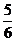
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com