
3.0-13.0s内电梯的位移 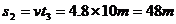 ⑧
⑧
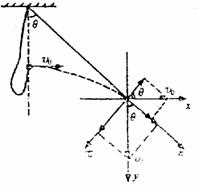
2.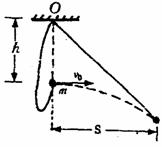 (13分)用长为L=1.0m的轻软绳将质量为m的小球悬于O点。然后拿住小球将其自悬点O下方距离为h=0.4m的位置以初速度v0水平抛出,当悬绳刚要伸直时,小球水平射程为S=0.8m,如图所示。设随后小球即做圆周运动,试计算小球运动到最低点时的速度多大(不计空气阻力,取g=10m/s2)
(13分)用长为L=1.0m的轻软绳将质量为m的小球悬于O点。然后拿住小球将其自悬点O下方距离为h=0.4m的位置以初速度v0水平抛出,当悬绳刚要伸直时,小球水平射程为S=0.8m,如图所示。设随后小球即做圆周运动,试计算小球运动到最低点时的速度多大(不计空气阻力,取g=10m/s2)
解:软绳刚伸直时与竖直方向的夹角为
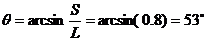
小球从抛出至绳伸直的过程中:
下落高度: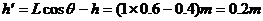
 飞行时间:
飞行时间:
水平速度: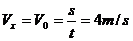
竖直速度: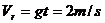
绳子张紧后沿绳方向(径向)速度为零,垂直绳方向(切向)速度不变(即小球随后以此切向速度开始作圆周运动),此速度为
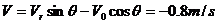
设圆周运动最低点速度为V′,对小球作圆周运动到达最低点的过程:
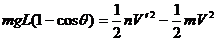
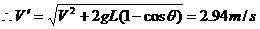
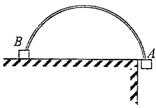 3.(14分)如图,在横截面为半圆形、半径为R的光滑柱面上,用一根不可伸长的细线两端分别系着物体A和B,且mA=2mB,让其由静止开始释放,试问:
3.(14分)如图,在横截面为半圆形、半径为R的光滑柱面上,用一根不可伸长的细线两端分别系着物体A和B,且mA=2mB,让其由静止开始释放,试问:
(1)物体B能否到达半圆顶点?
(2)若要B能过半圆顶点,mA应满足的条件是什么?(此时mA尚为着地)
解:(1)不能 (2)故所求的条件为: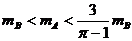
选系统为研究对象,据机械能守恒定律得:m1g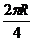 =m2gR+
=m2gR+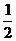 (m1+m2)v2 ①
(m1+m2)v2 ①
选m2为研究对象在最高点据牛顿第二定律得:m2g-N=m2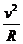 (N为m2所受支持力)②
(N为m2所受支持力)②
欲使m2通过圆柱体最高点,则:N>0 ③
联列①②③得: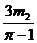 >m1,且应m1>m2.
故条件为:
>m1,且应m1>m2.
故条件为: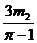 >m1>m2
>m1>m2
 4.(13分)一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度. 他将台秤放在电梯内,将重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断地运行,最后停在最高层,在整个过程中,他没有来得及将台秤的示数记录下来,假设在每个时间段内台秤的示数都是稳定的,重力加速度g取10m/s2
4.(13分)一位同学的家住在一座25层的高楼内,他每天乘电梯上楼,经过多次仔细观察和反复测量,他发现电梯启动后的运动速度符合如图所示的规律,他就根据这一特点在电梯内用台秤、重物和停表测量这座楼房的高度. 他将台秤放在电梯内,将重物放在台秤的托盘上,电梯从第一层开始启动,经过不间断地运行,最后停在最高层,在整个过程中,他没有来得及将台秤的示数记录下来,假设在每个时间段内台秤的示数都是稳定的,重力加速度g取10m/s2
|
时间/s |
台秤示数/kg |
|
电梯启动前 |
5.0 |
|
0-3.0 |
|
|
3.0-13.0 |
5.0 |
|
13.0-19.0 |
4.6 |
|
19.0以后 |
5.0 |
(1)电梯在0-3.0s时间段内台秤的示数应该是多少?
(2)根据测量的数据,计算该座楼房每一层的平均高度.
解:(1)由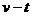 图象可知,电梯在13.0-19.0s内向上做匀减速运动.
图象可知,电梯在13.0-19.0s内向上做匀减速运动.
由牛顿第二定律: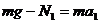 ①
①
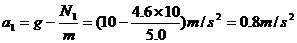 ②
②
匀速运动时的速度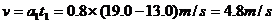 ③
③
0-3.0s内,电梯向上做匀加速运动,设其加速度为a2.
则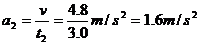 ④
④
由牛顿第二定律: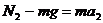 ⑤
⑤
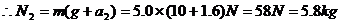 ⑥
⑥
即0-3.0s内台秤的示数应该为5.8kg
(2)0-3.0s内电梯的位移
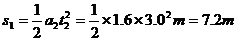 ⑦
⑦
1.(16分)一质量为m的质点,系于长为R的轻绳的一端,绳的另一端固定在空间的O点,假定绳是不可伸长的、柔软且无弹性的。今把质点从O点的正上方离O点的距离为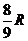 的O1点以水平的速度
的O1点以水平的速度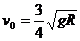 抛出。试求;
抛出。试求;
(1)轻绳即将伸直时,绳与竖直方向的夹角为多少?
(2)当质点到达O点的正下方时,绳对质点的拉力为多大?
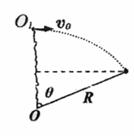 解:(1)设绳即将伸直时,绳与竖直方向的夹角为
解:(1)设绳即将伸直时,绳与竖直方向的夹角为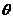 ,如图所示,则
,如图所示,则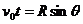 (1分)
(1分)
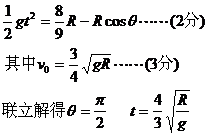
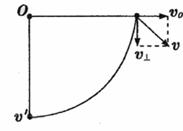 (2)绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度
(2)绳棚直时,绳刚好水平,如图所示.由于绳不可伸长,故绳绷直时,v0损失,质点仅有速度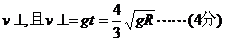
设质点到达O点正下方时,速度为v′,
根据机械能守恒守律有:
 ……(5分)
……(5分)
设此时绳对质点的拉力为T,
则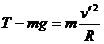 ……(6分)
……(6分)
联立解得: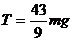 ……(7分)
……(7分)
5.(22分)如图所示,水平传送带AB长l=8.3m,质量为M=1kg的木块随传送带一起以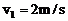 的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5。当木块运动至最左端A点时,一颗质量为m=20g的子弹以
的速度向左匀速运动(传送带的传送速度恒定),木块与传送带间的动摩擦因数μ=0.5。当木块运动至最左端A点时,一颗质量为m=20g的子弹以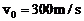 水平向右的速度正对射入木块并穿出,穿出速度u=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取
水平向右的速度正对射入木块并穿出,穿出速度u=50m/s,以后每隔1s就有一颗子弹射向木块,设子弹射穿木块的时间极短,且每次射入点各不相同,g取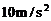 。求:
。求:
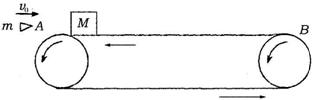
(1)在被第二颗子弹击中前,木块向右运动离A点的最大距离?
(2)木块在传送带上最多能被多少颗子弹击中?
(3)从第一颗子弹射中木块到木块最终离开传送带的过程中,子弹、木块和传送带这一系统所产生的热能是多少?( g取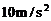 )
)
解:(1)第一颗子弹射入木块过程中动量守恒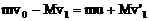 (1)
(1)
解得: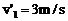 (2)
(2)
木块向右作减速运动 加速度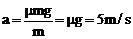 (3)
(3)
木块速度减小为零所用时间为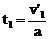 (4)
(4)
解得 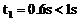 (5)
(5)
所以木块在被第二颗子弹击中前向右运动离A点最远时,速度为零,移动距离为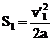 解得
解得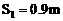 。(6)
。(6)
(2)在第二颗子弹射中木块前,木块再向左作加速运动,时间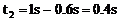 (7)
(7)
速度增大为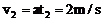 (恰与传递带同速) (8)
(恰与传递带同速) (8)
向左移动的位移为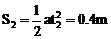 (9)
(9)
所以两颗子弹射中木块的时间间隔内,木块总位移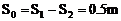 方向向右 (10)
方向向右 (10)
第16颗子弹击中前,木块向右移动的位移为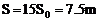 (11)
(11)
第16颗子弹击中后,木块将会再向右先移动0.9m,总位移为0.9m+7.5=8.4m>8.3m木块将从B端落下。
所以木块在传送带上最多能被16颗子弹击中。
(3)第一颗子弹击穿木块过程中产生的热量为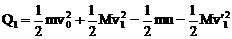 (12)
(12)
木块向右减速运动过程中板对传送带的位移为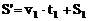 (13)
(13)
产生的热量为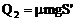 (14)
(14)
木块向左加速运动过程中相对传送带的位移为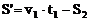 (15)
(15)
产生的热量为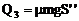 (16)
(16)
第16颗子弹射入后木块滑行时间为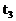 有
有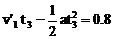 (17)
(17)
解得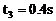 (18)
(18)
木块与传送带的相对位移为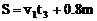 (19)
(19)
产生的热量为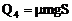 (20)
(20)
全过程中产生的热量为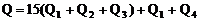
解得Q=14155.5J (21)
4.(13分)如图所示,AB是一段位于竖直平面内的光滑轨道,高度为h,末端B处的切线方向水平.一个质量为m的小物体P从轨道顶端A处由静止释放,滑到B端后飞出,落到地面上的C点,轨迹如图中虚线BC所示.已知它落地时相对于B点的水平位移OC=l.
现在轨道下方紧贴B点安装一水平传送带,传送带的右端与B的距离为l/2.当传送带静止时,让P再次从A点由静止释放,它离开轨道并在传送带上滑行后从右端水平飞出,仍然落在地面的C点.当驱动轮转动从而带动传送带以速度v匀速向右运动时(其他条件不变),P的落地点为D.(不计空气阻力)
(1)求P滑至B点时的速度大小;
(2)求P与传送带之间的动摩擦因数 ;
(3)求出O、D间的距离s随速度v变化的函数关系式.

解:(1)物体P在AB轨道上滑动时,物体的机械能守恒,根据机械能守恒定律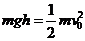 得物体P滑到B点时的速度为
得物体P滑到B点时的速度为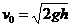 (3分)
(3分)
(2)当没有传送带时,物体离开B点后作平抛运动,运动时间为t,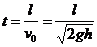 当B点下方的传送带静止时,物体从传送带右端水平抛出,在空中运动的时间也为t,水平位移为
当B点下方的传送带静止时,物体从传送带右端水平抛出,在空中运动的时间也为t,水平位移为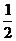 ,因此物体从传送带右端抛出的速度
,因此物体从传送带右端抛出的速度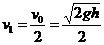 (2分).
(2分).
根据动能定理,物体在传送带上滑动时,有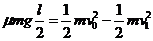 (1分).
(1分).
解出物体与传送带之间的动摩擦因数为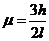 (1分).
(1分).
(3)当传送带向右运动时,若传送带的速度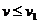 ,即
,即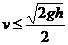 时,物体在传送带上一直做匀减速运动,离开传送带的速度仍为
时,物体在传送带上一直做匀减速运动,离开传送带的速度仍为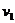 ,落地的水平位移为
,落地的水平位移为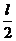 ,即s=l (2分).
,即s=l (2分).
当传送带的速度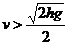 时,物体将会在传送带上做一段匀变速运动.如果尚未到达传送带右端,速度即与传送带速度相同,此后物体将做匀速运动,而后以速度v离开传送带.v的最大值
时,物体将会在传送带上做一段匀变速运动.如果尚未到达传送带右端,速度即与传送带速度相同,此后物体将做匀速运动,而后以速度v离开传送带.v的最大值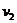 为物体在传送带上一直加速而达到的速度,即
为物体在传送带上一直加速而达到的速度,即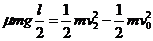 .由此解得
.由此解得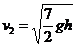 (1分).
(1分).
当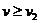 ,物体将以速度
,物体将以速度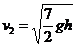 离开传送带,因此得O、D之间的距离为
离开传送带,因此得O、D之间的距离为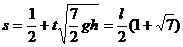 (1分).
(1分).
当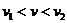 ,即
,即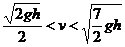 时,物体从传送带右端飞出时的速度为v,O、D之间的距离为
时,物体从传送带右端飞出时的速度为v,O、D之间的距离为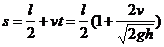 (1分). 综合以上的结果,得出O、D间的距离s随速度v变化的函数关系式为:
(1分). 综合以上的结果,得出O、D间的距离s随速度v变化的函数关系式为: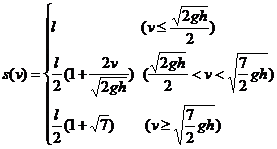 (1分)
(1分)
3.(18分)质量为m的小滑块自圆弧形轨道上端由静止滑下,如图所示,圆弧形轨道半径为R,高度为h. A点为弧形轨道与水平桌面的平滑连接点.滑块离开桌面后恰好落入静止在水平地面上的装满沙的总质量为M的小车中,桌面到小车上沙平面的高度也是h. 木块落入车内与沙面接触直到相对静止经过的较短时间为t. 试回答下列问题. 所有接触面的摩擦不计,重力加速度g已知,小车高度不计.
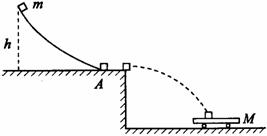 (1)滑块经过A点前后对轨道和桌面
(1)滑块经过A点前后对轨道和桌面
的压力F1、F2各多大?
(2)小车最终的速度是多大?
(3)滑块落入车中直到相对车静止的过
程中小车对地面的平均压力多大?
解:(1)滑块沿弧形轨道下滑的过程中
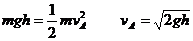 ①
①
经过A点前的瞬间: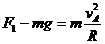 ②
②
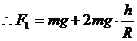 ③
③
经过A点后,滑块沿桌面匀速直线运动∴经过A点的瞬间: ④
④
(2)滑块离开桌面做平抛运动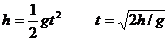
落入车内时,竖直方向分速度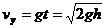 ⑤
⑤
水平方向分速度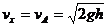
滑块与小车水平方向动量守恒.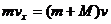 ⑥
⑥
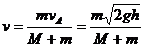 ⑦
⑦
(3)由动量定理: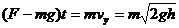 ⑧
⑧
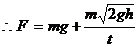 ⑨
⑨
小车对地的压力是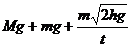 ⑩
⑩
评分标准:③⑦各1分,①②④⑤⑥⑧⑨⑩各2分,共18分
2.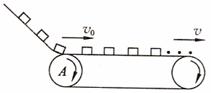 (10分)如图所示,在工厂的流水线上安装有水平传送带,用水平传送带传送工件,可以大大提高工作效率,水平传送带以恒定的速率
(10分)如图所示,在工厂的流水线上安装有水平传送带,用水平传送带传送工件,可以大大提高工作效率,水平传送带以恒定的速率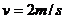 运送质量为
运送质量为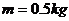 的工件,工件都是以
的工件,工件都是以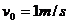 的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数
的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数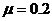 ,每当前一个工件在传送带上停止相对滑动时,后一个工件立即滑上传送带,取
,每当前一个工件在传送带上停止相对滑动时,后一个工件立即滑上传送带,取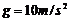 ,求:
,求:
(1)工件滑上传送带后多长时间停止相对滑动
(2)在正常运行状态下传送带上相邻工件间的距离
(3)在传送带上摩擦力对每个工件做的功
(4)每个工件与传送带之间由于摩擦产生的内能
解:(1)工作停止相对滑动前的加速度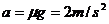 ①
①
由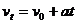 可知:
可知: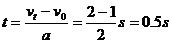 ②
②
(2)正常运行状态下传送带上相邻工件间的距离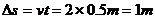 ③
③
(3)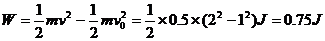 ④
④
(4)工件停止相对滑动前相对于传送带滑行的距离
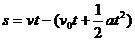
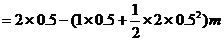
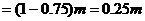 ⑤
⑤
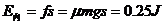 ⑥
⑥
评分标准:①③④⑤式各2分 ②⑥式各1分,共10分
1.(14分)如图所示,水平传送带水平段长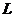 =6米,两皮带轮直径均为D=0.2米,距地面高度H=5米,与传送带等高的光滑平台上有一个小物体以v0=5m/s的初速度滑上传送带,物块与传送带间的动摩擦因数为0.2,g=10m/s2,求:
=6米,两皮带轮直径均为D=0.2米,距地面高度H=5米,与传送带等高的光滑平台上有一个小物体以v0=5m/s的初速度滑上传送带,物块与传送带间的动摩擦因数为0.2,g=10m/s2,求:
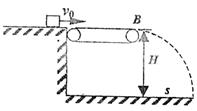 (1)若传送带静止,物块滑到B端作平抛运动的水平距离S0。
(1)若传送带静止,物块滑到B端作平抛运动的水平距离S0。
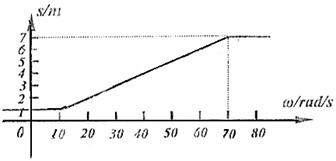
(2)当皮带轮匀速转动,角速度为ω,物体平抛运动水平位移s;以不同的角速度ω值重复上述过程,得到一组对应的ω,s值,设皮带轮顺时针转动时ω>0,逆时针转动时ω<0,并画出s-ω关系图象。
解:(1)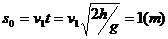
(2)综上s-ω关系为: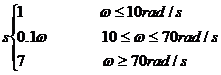
15、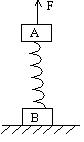 如图所示,两个质量均为m的重物A、B用劲度系数为k的轻弹簧连结后,竖直放到水平地面上,B与地面接触,开始A、B均静止。今用竖直向上拉力F作用在A上,且F = mg,下列说法正确的是
如图所示,两个质量均为m的重物A、B用劲度系数为k的轻弹簧连结后,竖直放到水平地面上,B与地面接触,开始A、B均静止。今用竖直向上拉力F作用在A上,且F = mg,下列说法正确的是
A.A上升最大高度为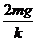 B.A上升时间为
B.A上升时间为 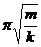
C.A上升过程中,该系统机械能守恒
D.A上升过程中,弹簧对A弹力冲量为 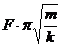
解:AB。
本题主要考查能量转换关系、机械能守恒的条件、简谐振动的周期及冲量的计算等。开始时,受F力作用时,弹性势能转变成弹簧恢复原长时物体的动能,物体再上升时,物体的动能又转变成弹性势能,物体增加的重力势能由外力F做功提供,上升时机械能不守恒。开始弹簧被压缩,设压缩量为x,则kx = mg,x = mg/k,物体再上升的高度仍为x,故物体上升的最大高度为2x,则2x=2mg/k。物体做简谐振动的周期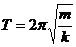 ,而物体从受F力作用开始,上升到最大高度这段时间为
,而物体从受F力作用开始,上升到最大高度这段时间为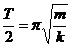 。在上升过程中,弹簧对A的作用力在前
。在上升过程中,弹簧对A的作用力在前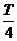 内方向向上,后
内方向向上,后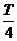 内对A的作用力方向向下,其大小不断变化,但总冲量为零。
内对A的作用力方向向下,其大小不断变化,但总冲量为零。
14.(10分)如图所示,A、B是两相同的小物块,C是轻弹簧,用一根细线连接A、B使弹簧C处于压缩状态,然后放置在光滑的水平桌面上。提供的测量器材有天平和刻度尺。试设计一个测定弹簧此时弹性势能Ep的实验方案,写出实验中应测定的物理量(同时用相应的字母表示),并写出计算弹簧弹性势能Ep的表达式(用测得物理量的字母表示)。
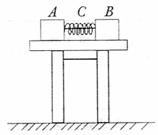 解:应测量的数据有 :
解:应测量的数据有 :
①小物块的质量m
②两小物块的落地点之间的距离s
③桌面的高度h
④桌面的宽度d(5分,其他做法可行的也给5分)
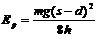 (5分,其他做法可行的也给5分)
(5分,其他做法可行的也给5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com