
3.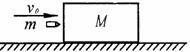 (16分)如图,在光滑的水平桌面上,静放着一质量为980g的长方形匀质木块,现有一颗质量为20g的子弹以300m/s的水平速度沿其轴线射向木块,结果子弹留在木块中没有射出,和木块一起以共同的速度运动。已知木块沿子弹运动方向的长度为10cm,子弹打进木块的深度为6cm。设木块对子弹的阻力保持不变。
(16分)如图,在光滑的水平桌面上,静放着一质量为980g的长方形匀质木块,现有一颗质量为20g的子弹以300m/s的水平速度沿其轴线射向木块,结果子弹留在木块中没有射出,和木块一起以共同的速度运动。已知木块沿子弹运动方向的长度为10cm,子弹打进木块的深度为6cm。设木块对子弹的阻力保持不变。
(1)求子弹和木块的共同速度以及它们在此过程中所增加的内能。
(2)若子弹是以400m/s的水平速度从同一方向水平射向该木块的,则它能否射穿该木块?
解:(1)设子弹的初速度为v0,射入木块的共同速度为v.以子弹和木块为系统,由动量守恒定律有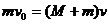 (2分)解得
(2分)解得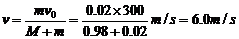 (2分)
(2分)
此过程系统所增加的内能
(2)设以v0′=400m/s的速度刚好能够射穿材质一样厚度为d′的另一个木块.则对以子弹和木块组成的系统,由动量守恒定律有:
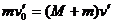
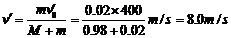
此过程系统所损耗的机械能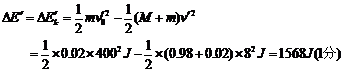
由功能关系有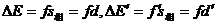 (2分)
(2分)
两式相比即有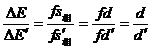
于是有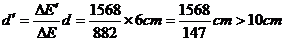 (3分)
(3分)
因为d′>10cm,所以能够穿透此木块.(1分)
1.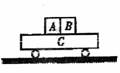 (14分)如图所示,A、B质量分别为
(14分)如图所示,A、B质量分别为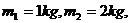 置于小车C上。小车质量
置于小车C上。小车质量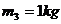 ,AB间粘有少量炸药,AB与小车间的动摩擦因数均为0.5,小车静止在光滑水平面上,若炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能。A、B始终在小车上表面水平运动,求:
,AB间粘有少量炸药,AB与小车间的动摩擦因数均为0.5,小车静止在光滑水平面上,若炸药爆炸释放的能量有12J转化为A、B的机械能,其余的转化为内能。A、B始终在小车上表面水平运动,求:
(1)A、B开始运动的初速度各是多少?
(2)A、B在小车上滑行时间各是多少?
解:(1)设A、B分开时速度分别为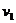 和
和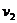 。
。
A、B爆炸过程动量守恒,则有: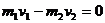 (1)
(1)
依题意与能的转化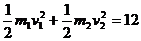 (2)
(2)
联列可以解得: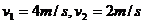
(2)由题意可以判断B以C上先停下来,A后停下来,对于B依动量定理有:
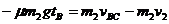 (3)(
(3)(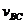 为B在C上停下时B、C的共同速度)
为B在C上停下时B、C的共同速度)
对C依动量定理有:(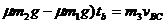 (4)
(4)
代入数据可以解得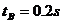 由题意与动量守恒可得当A在C上静止时,A、B、C均处于静止状态。对A由动量定理有:
由题意与动量守恒可得当A在C上静止时,A、B、C均处于静止状态。对A由动量定理有: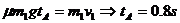
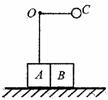 2.(12分)如图所示,质量均为M的木块A和B,并排放在光滑水平面上,A上固定一竖直轻杆,轻杆上端的小钉(质量不计)O上系一长度为L的细线,细线另一端系一质量为m的球C,现将C球拉起使细线水平伸直,并由静止释放C球(C球不与直杆相碰)。求:
2.(12分)如图所示,质量均为M的木块A和B,并排放在光滑水平面上,A上固定一竖直轻杆,轻杆上端的小钉(质量不计)O上系一长度为L的细线,细线另一端系一质量为m的球C,现将C球拉起使细线水平伸直,并由静止释放C球(C球不与直杆相碰)。求:
(1)两木块刚分离时,A、B、C的速度各多大?
(2)两木块分离后,小球偏离竖直方向的最大偏角?
解:(1)小球C下落到最低点时,AB开始分离,此过程整个分流水平方向动量守恒。机械能守恒
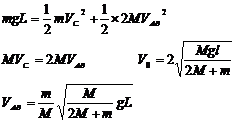
(2)选A、B、C研究对象 0=MVAB-(M+m)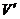
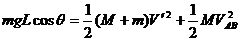
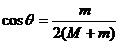
 8.浙江模拟题在光滑的水平面上有一块质量
8.浙江模拟题在光滑的水平面上有一块质量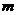 =1kg的长木板,木板上相距
=1kg的长木板,木板上相距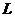 =1.2m处各放一个质量
=1.2m处各放一个质量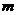 =1kg的小木块A和B(这两个小木块可当作质点),现分别给A木块向右的速度
=1kg的小木块A和B(这两个小木块可当作质点),现分别给A木块向右的速度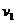 =5m/s,B木块向左的速度
=5m/s,B木块向左的速度 =2m/s,两木块沿同一直线相向运动,两木块与木板间的动摩擦因数
=2m/s,两木块沿同一直线相向运动,两木块与木板间的动摩擦因数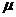 =0.50,两木块相遇时作弹性碰撞(碰撞时间极短,且相互交换速度)。(
=0.50,两木块相遇时作弹性碰撞(碰撞时间极短,且相互交换速度)。(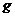 取10m/s2)求:
取10m/s2)求:
(1)如A、B始终在木板上,两木块间的最大距离。
(2)要使A、B始终在木板上,木板的长度至少要多长。
解法1:两木块在木板上滑动时的加速度为 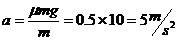
经t s两木块相遇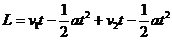
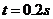
两木块相遇前瞬间的速度分别为 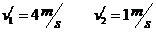
两木块相碰后速度交换 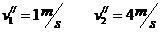
根据动量守恒定律,可求出两木块与木板的共同速度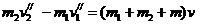
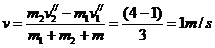
A、B两木块相对静止时相距最远 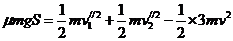
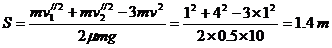
解法2:两木块从开始滑动到相对静止过程中,ABC组成的系统动量守恒:
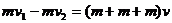
从能的转化和守恒来看,减小的机械能全部用来克服摩擦阻力做功转化为热能,且一对摩擦阻力做功的代数和与接触面间的相对滑动的路程有关,令两物体最终相距为S则有:
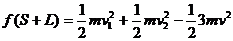 ,同理可解得:S=1.4m
,同理可解得:S=1.4m
(2)A、B两木块相遇时A向右的位移为 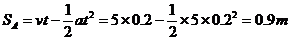
A、B相碰后,A向左的速度减小到零时,向左的位移为 
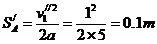
木板的最短长度为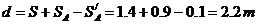

9.如图所示,一块足够长的木块,放在光滑的水平面上,在木板上自左向右放有序号是1,2,3,…,n的木块,所有木块的质量均为m,与木板间的动摩擦因数都相同。开始时,木板静止不动,第1,2,3,…,n号木板的初速度分别是v0,2v0,3v0,…,nv0,方向都向右。木板的质量与所有木块的总质量相等。最终所有木块与木块以共同速度匀速运动。设木块之间均无相互碰撞,木板足够长。求:
(1) 所有木块与木板一起匀速运动的速度vn
(2) 第1号木块与木板刚好相对静止时的速度v1
(3) 通过分析与计算说明第k号(n > k)木块的最小速度vk。
解: (1)木板的质量为M=nm,设最终所有木块和木板一起匀速运动的速度为vn,由动量守恒定律得m(v0 + 2v0 + …+nv0)
= (nm + M)vn,解得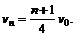
(2)设第1号木块与木板相对静止时速度为v1,该木块速度的减小量为△v = v0 –
v1。由于其他木块与第1号木块有相同的加速度,这段时间内的所有木块的速度都减小△v = v0 – v1。由动量守恒知,木板动量的增加量等于所有木块动量的减小量,即Mv1 = nm(v0 – v1),解得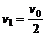 。
。
(3)当第k号木块与木板速度相同时,第k号木块的速度减为最小,此时第1,2,3…k号木块及木块的速度均为vk,而第k + 1,k + 2,…n号木块动量的减小值均为(n-k)m(kv0 – vk),由动量守恒定律知,它应等于系统其余部分动量的增加量,即(km + M)vk – m(1+2+3+…+k)v0
= (n – k) m (kv0 – vk)。解得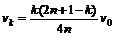 ,其中n > k。
,其中n > k。
7.在绝缘水平面上放一质量m=2.0×10-3kg的带电滑块A,所带电荷量q=1.0×10-7C.在滑块A的左边l=0.3m处放置一个不带电的绝缘滑块B,质量M=4.0×10-3kg,B与一端连在竖直墙壁上的轻弹簧接触(不连接)且弹簧处于自然状态,弹簧原长S=0.05m.如图所示,在水平面上方空间加一水平向左的匀强电场,电场强度的大小为E=4.0×105N/C,滑块A由静止释放后向左滑动并与滑块B发生碰撞,设碰撞时间极短,碰撞后两滑块结合在一起共同运动并一起压缩弹簧至最短处(弹性限度内),此时弹性势能E0=3.2×10-3J,两滑块始终没有分开,两滑块的体积大小不计,与水平面间的动摩擦因数均为μ=0.5,g取10m/s2.求:
(1)两滑块碰撞后刚结合在一起的共同速度v;
(2)两滑块被弹簧弹开后距竖直墙壁的最大距离s.
解:(1)设两滑块碰前A的速度为v1,由动能定理有: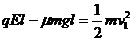
解得:v1=3m/s
A、B两滑块碰撞,由于时间极短动量守恒,设共同速度为v 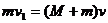
解得:v=1.0m/s
(2)碰后A、B一起压缩弹簧至最短,设弹簧压缩量为x1,由动能定理有:
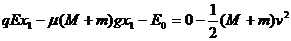
解得:x1=0.02m
设反弹后A、B滑行了x2距离后速度减为零,由动能定理得:
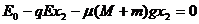 解得:x2≈0.05m
解得:x2≈0.05m
以后,因为qE>μ(M+m)g,滑块还会向左运动,但弹开的距离将逐渐变小,所以,最大距离为:S=x2+s-x1=0.05m+0.05m-0.02m
5. 如图所示,P是固定的竖直挡板,A置于光滑水平面上的平板小车(小车表面略低于挡板下端),B是放在小车最左端表面上的一个可视为质点的小物块。开始时,物块随小车一起以相同的水平速度向左运动,接着物块与挡板发生了第一次碰撞,碰后物块相对于静止时的位置离小车最左端的距离等于车长的3/4,此后物块又与挡板发生了多次碰撞,最后物块给恰未从小车上没落。若物块与小车表面间的动摩擦因素是个定值,物块与挡板发生碰撞时无机械能损失且碰撞时间极短暂,试确定小车与物块的质量关系。
如图所示,P是固定的竖直挡板,A置于光滑水平面上的平板小车(小车表面略低于挡板下端),B是放在小车最左端表面上的一个可视为质点的小物块。开始时,物块随小车一起以相同的水平速度向左运动,接着物块与挡板发生了第一次碰撞,碰后物块相对于静止时的位置离小车最左端的距离等于车长的3/4,此后物块又与挡板发生了多次碰撞,最后物块给恰未从小车上没落。若物块与小车表面间的动摩擦因素是个定值,物块与挡板发生碰撞时无机械能损失且碰撞时间极短暂,试确定小车与物块的质量关系。
解:设小车、物块的质量分别为M和m,车长为L,物块与小车间的动摩擦因素为μ,初速度为v0。第一次碰后由于无机械能损失,因此物块的速度方向变为向右,大小仍为v0,此后它与小车相互作用,当两者速度相等时(由题意知,此速度方向必向左,即必须有M>m),有该次相对车的最大位移l
对物块、小车系统由动量守恒定律有(M-m)v0=(M+m)v ①
由于某种原能量守恒有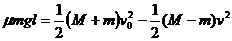 ②
②
多次碰撞后,物块恰未从小车上滑落,表明最后当物块运动到小车最右端时两者刚好停止运动(或者速度同时趋于零)
对物块、小车系统由动量守恒定律有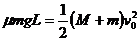 ③
③
而 l=3L/4 ④ 由②③④得v0=2v 代入①解得M=3m
三、电场条件下的木块运动类
 6.在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小
6.在一个水平面上建立x轴,在过原点O垂直于x轴的平面的右侧空间有一个匀强电场,场强大小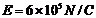 ,方向与x轴正方向相同,在O处放一个带电量
,方向与x轴正方向相同,在O处放一个带电量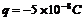 ,质量m=10g的绝缘物块。物块与水平面间的动摩擦因数
,质量m=10g的绝缘物块。物块与水平面间的动摩擦因数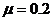 ,沿x轴正方向给物块一个初速度
,沿x轴正方向给物块一个初速度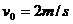 ,如图所示,求物块最终停止时的位置。(g取10m/s2)
,如图所示,求物块最终停止时的位置。(g取10m/s2)
解:物块在水平面受摩擦力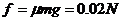
物块受电场力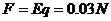
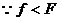
∴物块不可能在右侧静止,向右减速为零后向左加速离开电场,在左侧减速为零。设在O点右侧S处速度减为零,在O点左侧d处停止,则
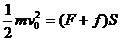 (1)
(1)
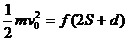 (2)
(2)
联(1)(2)解得 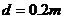

2.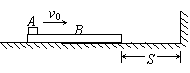 重庆一中 一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为S=0.5m.一个质量为m=1kg的小物体A以初速度
重庆一中 一质量M=2kg的长木板B静止在光滑的水平面上,B的右端与竖直挡板的距离为S=0.5m.一个质量为m=1kg的小物体A以初速度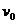 =6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端。设定物体A可视为质点,A、B间的动摩擦因数μ=0.2,B与竖直挡板碰撞时间极短且碰撞过程中无机械能损失,g取10m/s2.求:
=6m/s从B的左端水平滑上B,当B与竖直挡板每次碰撞时,A都没有到达B的右端。设定物体A可视为质点,A、B间的动摩擦因数μ=0.2,B与竖直挡板碰撞时间极短且碰撞过程中无机械能损失,g取10m/s2.求:
(1)B与竖直挡板第一次碰撞前的瞬间,A、B的速度值各是多少?
(2)最后要使A不从B上滑下,木板B的长度至少是多少?(最后结果保留三位有效数字.)
解:(1)设A、B达到共同速度为v1时,B向右运动距离为S1
由动量守恒定律有 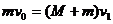 由动能定理有
由动能定理有 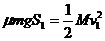
联立解得 S1=2m
由于S=0.5m<2m,可知B与挡板碰撞时,A、B还未达到共同速度。设B与挡板碰撞前瞬间A的速度为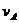 ,B的速度为
,B的速度为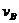 ,则由动量守恒定律有
,则由动量守恒定律有 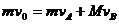
由动能定理有 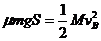 联立解得
联立解得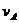 =4m/s、
=4m/s、 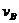 =1m/s
=1m/s
(2)B与挡板第一次碰后向左减速运动,当B速度减为零时,B向左运动的距离设为SB,由动能定理有 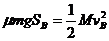 由上式解得 SB=0.5m
由上式解得 SB=0.5m
在A的作用下B再次反向向右运动,设当A、B向右运动达到共同速度v2时B向右运动距离为S2,由动量守恒定律有 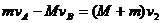
由动能定理有  解得
解得 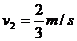
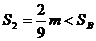
故A、B以共同速度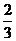 m/s向右运动,B第二次与挡板碰撞后,以原速率反弹向左运动.此后由于系统的总动量向左,故最后A、B将以共同速度v3向左匀速运动.
m/s向右运动,B第二次与挡板碰撞后,以原速率反弹向左运动.此后由于系统的总动量向左,故最后A、B将以共同速度v3向左匀速运动.
由动量守恒定律有 (M-m)v2=(M+m)v3
解得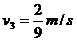
设A在B上运动的总量程为L(即木板B的最小长度),由系统功能关系得:
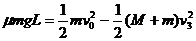 代入数据解得 L=8.96m
代入数据解得 L=8.96m
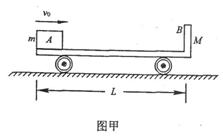 3.如图甲所示,小车B静止在光滑水平面上,一个质量为m的铁块A(可视为质点),以水平速度v0=4.0m/s从左端滑上小车B,然后与小车右端挡板碰撞,最后恰好停在小车车面的中点.已知小车车面长L=1m,小车质量M=3m.设A与挡板碰撞无机械能损失,碰撞时间可忽略不计,g取10m/s2.求:
3.如图甲所示,小车B静止在光滑水平面上,一个质量为m的铁块A(可视为质点),以水平速度v0=4.0m/s从左端滑上小车B,然后与小车右端挡板碰撞,最后恰好停在小车车面的中点.已知小车车面长L=1m,小车质量M=3m.设A与挡板碰撞无机械能损失,碰撞时间可忽略不计,g取10m/s2.求:
 (1)A、B最终速度的大小;
(1)A、B最终速度的大小;
(2)铁块A与小车B之间的动摩擦因数;
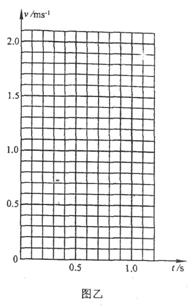
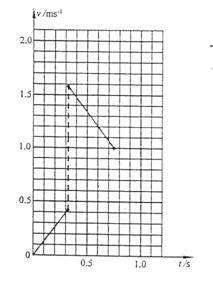
(3)铁块A与小车B的挡板相碰撞前后小车B的速度大小,并在图乙坐标中画出在A、B相对滑动过程中小车B相对地面的速度v-t图线.
解:(1)对A、B系统,由动量守恒定律:
Mv0=(M+m)v 得v=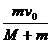 =1m/s
=1m/s
(2)A、B系统,由动量定理,对全过程有μmg1.5L=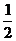 mv
mv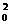 -
-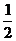 (M+m)v2
(M+m)v2
解得μ=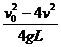 =0.4
=0.4
(3)设A、B碰撞前速度分别为v10和v20
对系统动量守恒mv0=mv1+Mv2
对系统能量转化和守恒μmgL=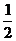 mv
mv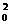 -
-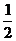 mv
mv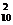 -
-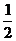 Mv
Mv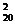
带入数据联立方程,解得v10=1+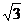 =2.732m/s(舍v10=1-
=2.732m/s(舍v10=1-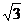 =-0.732m/s)
=-0.732m/s)
v20=1-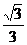 =0.423m/s
=0.423m/s
该过程小车B做匀加速运动,μmg=MαM aM=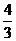 m/s2
m/s2
v20=aMt1 t1=0.317s
A、B相碰,设A、B碰后A的速度为v1和v2
A,对系统动量守恒mv0=mv1+Mv2
 对系统机械能守恒
对系统机械能守恒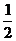 mv
mv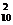 -
-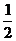 Mv
Mv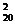 =
=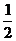 mv
mv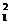 +
+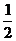 Mv
Mv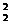
带入数据联立方程,解得v1=1-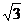 =-0.732m/s
=-0.732m/s
(舍v1=1+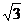 m/s)“-”说明方向向左
m/s)“-”说明方向向左
v2=1+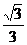 =1.577m/s
=1.577m/s
该过程小车B做匀减速运动,-μmg=MaM aM=-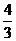 m/s2
m/s2
到最终相对静止v=v2+aMt2
t2=0.433s
所以,运动的总时间为t=t1+t2=O.75s
小车B的v-t图如图所示:
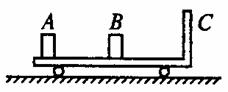 4.2005深圳市第一次调研考试:如图所示,长为2L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有挡板,车的质量
4.2005深圳市第一次调研考试:如图所示,长为2L的板面光滑且不导电的平板小车C放在光滑水平面上,车的右端有挡板,车的质量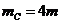 .今在静止的平板车的左端放一个带电荷量为+q、质量为
.今在静止的平板车的左端放一个带电荷量为+q、质量为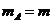 的金属块A,另将一绝缘小物块B放在平板车的中央,物块B的质量
的金属块A,另将一绝缘小物块B放在平板车的中央,物块B的质量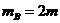 .在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,A以速度
.在整个空间加上一个水平方向的匀强电场时,金属块A由静止开始向右运动,A以速度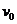 与B发生碰撞,碰后A以
与B发生碰撞,碰后A以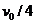 的速度反弹回来,B以一定速度沿平板向右运动与C车的挡板相碰.碰后小车的速度等于碰前物块B速度的一半.物块A、B均视为质点,A、B相碰时的相互作用力远大于电场力.求:
的速度反弹回来,B以一定速度沿平板向右运动与C车的挡板相碰.碰后小车的速度等于碰前物块B速度的一半.物块A、B均视为质点,A、B相碰时的相互作用力远大于电场力.求:
(1)匀强电场的场强大小和方向;
(2)若A第二次和B相碰,判断是在B与C相碰之前还是相碰之后?
(3)A从第一次与B相碰到第二次与B相碰的这段时间内,电场力对A做的功。
解:(1)E的方向向右,A与B碰撞前过程由动能定理得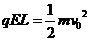
所以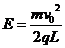
(2)A和B碰撞过程,根据动量守恒有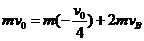 所以
所以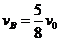
B运动到C所用时间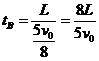
A运动到C所用时间,由运动学和动力学公式得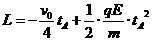
解得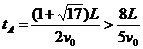
故A第二次和B相碰,一定是在B和C相碰之后。
(3)B和C相碰,动量守恒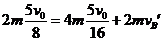 所以
所以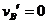 故W=qEL
故W=qEL
 1.如图所示,质量为M = 4kg的木板静置于足够大的水平地面上,木板与地面间的动因数μ = 0.01,板上最左端停放着质量为m = 1kg可视为质点的电动小车,车与木板的挡板相距L = 5m.车由静止开始从木板左端向右做匀加速运动,经时间t = 2s,车与挡板相碰,碰撞时间极短且碰后电动机的电源切断,车与挡板粘合在一起,求碰后木板在水平地上滑动的距离。
1.如图所示,质量为M = 4kg的木板静置于足够大的水平地面上,木板与地面间的动因数μ = 0.01,板上最左端停放着质量为m = 1kg可视为质点的电动小车,车与木板的挡板相距L = 5m.车由静止开始从木板左端向右做匀加速运动,经时间t = 2s,车与挡板相碰,碰撞时间极短且碰后电动机的电源切断,车与挡板粘合在一起,求碰后木板在水平地上滑动的距离。
解:设木板不动,电动车在板上运动的加速度为a0。
由 L = a0t2 得 a0 = 2.5m/s2
此时木板使车向右运动的摩擦力 F = ma0 = 2.5N
木板受车向左的反作用力 Fˊ = F = 2.5N
木板受地面向右最大静摩擦力 Ff = μ (M + m)g = 0.5N
Fˊ>Ff所以木板不可能静止,将向左运动
设电动车向右运动加速度为a1,木板向左运动加速度为a2,碰前电动车速度为υ1,木板速度为υ2,碰后共同速度为υ,两者一起向右运动s而停止,则a1t2 + a2t22 = L
对木板 F – μ (m + M )g = Ma2 对电动车 F = Fˊ = ma 而 υ1 = a1t υ2 = a2t 两者相碰时动量守恒,以向右为正方向,有mυ1 - Mυ2 = (m + M )υ
由动能定理得 - μ (m + M )gs = 0 - (m + M )υ2
代入数据,解得s = 0.2m
6.(类似绳的牵引问题)一列火车车头要拉十几节完全相同的车厢,每节车厢的质量是m,列车头的质量是一节车厢质量的3倍。列车静止于一水平的轨道上,车头与第1节车厢间、相邻辆车厢间用相同的车钩连接,车钩是松弛的、有一个相同的间距d。不计阻力,车头以恒力F拉列车起动,每节车厢由于连接车钩的撞击拉紧而依次进入运动状态。求:
(1)第一节车厢刚被拉动时的速度。
(2)第n节车厢刚被拉动时的速度。
(3)第几节车厢刚被拉动时的速度最大。
解:车头的拉力每次拉动车头或车厢时,均通过相同的距离d,所做的功都相同,设为W。
(1)车头第一次加速后,根据动能定理有: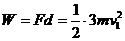 ①
①
车头拉动第1节车厢后,设其共同速度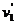 ,在此过程中,对车头和第一节车厢整体,根据动量守恒定律有:
,在此过程中,对车头和第一节车厢整体,根据动量守恒定律有: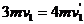 ② 联立①②可得:
② 联立①②可得: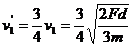 ③
③
(2)由①式可得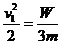 ④
④
设车头第2次加速后,其速度为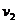 ,根据动能定理有:
,根据动能定理有: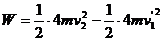 ⑤
⑤
车头拉动第2节车厢至达到共同速度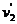 ,在此过程中,根据动量守恒定律有:
,在此过程中,根据动量守恒定律有: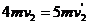 ⑥
⑥
联立②④⑤三式得: 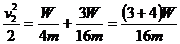 ⑦(4分)
⑦(4分)
设车头第3次加速后,其速度为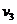 ,根据动能定理有:
,根据动能定理有: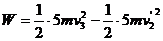 ⑧
⑧
车头拉动第3节车厢至达到共同速度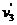 ,在此过程中,根据动量守恒定律有:
,在此过程中,根据动量守恒定律有: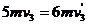 ⑨
⑨
联立⑥⑦⑧三式得: 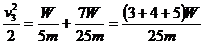 ⑩(4分)
⑩(4分)
……
设车头第n次加速后,其速度为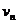 ,依次类推,可得:
,依次类推,可得: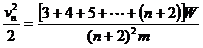 (11)
(11)
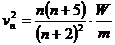 (12)
(12)
车头拉动第n节车厢至达到共同速度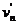 ,在此过程中,根据动量守恒定律有:
,在此过程中,根据动量守恒定律有:
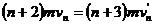 (13)
(13)
联立(12)(13)式得: 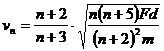
(3)设车头第n此加速后速度最大,由(12)式有: 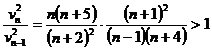 ,即:
,即: 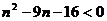 。而
。而 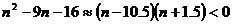 ,则n<10.5,取n=10,即
,则n<10.5,取n=10,即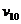 最大。
最大。
5.(20分)有许多个质量都为m的木块互相靠着沿一直线排列于光滑水平面上,每两个相邻的木块均用长为L的柔绳连接着。现用一恒力F沿排列方向拉第一块木块,以后各个木块依次被牵动。求第n个木块被牵动时的速度。
解:对第一个木块,由动能定理得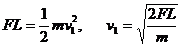
在拉动第二个木块的过程中,动量守恒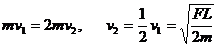 ,
,

 ,
……
,
……
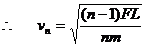
13.0-19.0s内电梯的位移 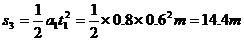 ⑨
⑨
总高度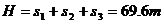
平均高度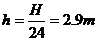 ⑩
⑩
评分标准:①④⑤式各2分 ②③⑥⑦⑧⑨⑩式各1分 共13分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com