
题型1:集合的概念
(2009湖南卷理)某班共30人,其中15人喜爱篮球运动,10人喜爱兵乓球运动,8人对这两项运动都不喜爱,则喜爱篮球运动但不喜爱乒乓球运动的人数为_12__
答案 :12
解析 设两者都喜欢的人数为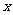 人,则只喜爱篮球的有
人,则只喜爱篮球的有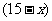 人,只喜爱乒乓球的有
人,只喜爱乒乓球的有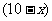 人,由此可得
人,由此可得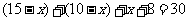 ,解得
,解得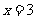 ,所以
,所以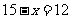 ,即 所求人数为12人。
,即 所求人数为12人。 

例1.(2009广东卷理)已知全集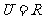 ,集合
,集合 和
和
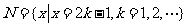 的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有 ( )
的关系的韦恩(Venn)图如图1所示,则阴影部分所示的集合的元素共有 ( )
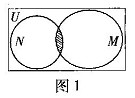
A. 3个 B. 2个
C. 1个 D. 无穷多个
答案 B
解析 由 得
得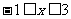 ,则
,则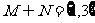 ,有2个,选B.
,有2个,选B.
例2.(2009山东卷理)集合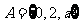 ,
,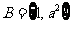 ,若
,若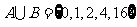 ,则
,则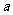 的值
的值
为 ( )
A.0 B.1 C.2 D.4
答案 D
解析 ∵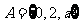 ,
,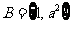 ,
,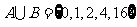 ∴
∴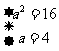 ∴
∴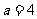 ,故选D.
,故选D.
[命题立意]:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.
题型2:集合的性质
例3.(2009山东卷理)集合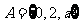 ,
,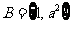 ,若
,若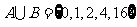 ,则
,则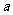 的值为 ( )
的值为 ( )
A.0 B.1 C.2 D.4
答案 D
解析 ∵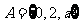 ,
,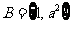 ,
,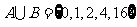 ∴
∴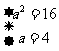 ∴
∴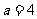 ,故选D.
,故选D.
[命题立意]:本题考查了集合的并集运算,并用观察法得到相对应的元素,从而求得答案,本题属于容易题.
随堂练习
1.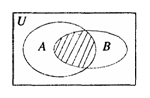 ( 广东地区2008年01月份期末试题汇编)设全集U=R,A={x∈N︱1≤x≤10},B={ x∈R︱x 2+
x-6=0},则下图中阴影表示的集合为 ( )
( 广东地区2008年01月份期末试题汇编)设全集U=R,A={x∈N︱1≤x≤10},B={ x∈R︱x 2+
x-6=0},则下图中阴影表示的集合为 ( )
A.{2} B.{3}
C.{-3,2} D.{-2,3}
5.集合的简单性质:
(1)
(2)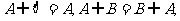
(3)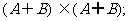
(4)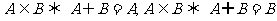 ;
;
(5)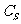 (A∩B)=(
(A∩B)=(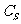 A)∪(
A)∪(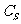 B),
B),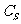 (A∪B)=(
(A∪B)=(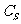 A)∩(
A)∩(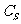 B)。
B)。
4.交集与并集:
(1)一般地,由属于集合A且属于集合B的元素所组成的集合,叫做集合A与B的交集。交集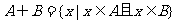 。
。
(2)一般地,由所有属于集合A或属于集合B的元素所组成的集合,称为集合A与B的并集。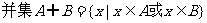

注意:求集合的并、交、补是集合间的基本运算,运算结果仍然还是集合,区分交集与并集的关键是“且”与“或”,在处理有关交集与并集的问题时,常常从这两个字眼出发去揭示、挖掘题设条件,结合Venn图或数轴进而用集合语言表达,增强数形结合的思想方法。
3.全集与补集:
(1)包含了我们所要研究的各个集合的全部元素的集合称为全集,记作U;
(2)若S是一个集合,A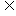 S,则,
S,则,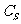 =
=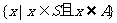 称S中子集A的补集;
称S中子集A的补集;
(3)简单性质:1)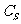 (
(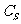 )=A;2)
)=A;2)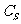 S=
S=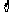 ,
,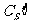 =S
=S
2.集合的包含关系:
(1)集合A的任何一个元素都是集合B的元素,则称A是B的子集(或B包含A),记作A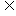 B(或
B(或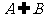 );
);
 集合相等:构成两个集合的元素完全一样。若A
集合相等:构成两个集合的元素完全一样。若A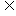 B且B
B且B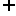 A,则称A等于B,记作A=B;若A
A,则称A等于B,记作A=B;若A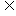 B且A≠B,则称A是B的真子集,记作A B;
B且A≠B,则称A是B的真子集,记作A B;
(2)简单性质:1)A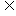 A;2)
A;2)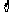
 A;3)若A
A;3)若A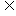 B,B
B,B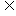 C,则A
C,则A C;4)若集合A是n个元素的集合,则集合A有2n个子集(其中2n-1个真子集);
C;4)若集合A是n个元素的集合,则集合A有2n个子集(其中2n-1个真子集);
1.集合:某些指定的对象集在一起成为集合
(1)集合中的对象称元素,若a是集合A的元素,记作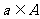 ;若b不是集合A的元素,记作
;若b不是集合A的元素,记作 ;
;
(2)集合中的元素必须满足:确定性、互异性与无序性;
确定性:设A是一个给定的集合,x是某一个具体对象,则或者是A的元素,或者不是A的元素,两种情况必有一种且只有一种成立;
互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;
无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关;
(3)表示一个集合可用列举法、描述法或图示法;
列举法:把集合中的元素一一列举出来,写在大括号内;
描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
具体方法:在大括号内先写上表示这个集合元素的一般符号及取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征。
注意:列举法与描述法各有优点,应该根据具体问题确定采用哪种表示法,要注意,一般集合中元素较多或有无限个元素时,不宜采用列举法。
(4)常用数集及其记法:
非负整数集(或自然数集),记作N;
正整数集,记作N*或N+;
整数集,记作Z;
有理数集,记作Q;
实数集,记作R。
有关集合的高考试题,考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用Venn图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练。考试形式多以一道选择题为主,分值5分。
预测2010年高考将继续体现本章知识的工具作用,多以小题形式出现,也会渗透在解答题的表达之中,相对独立。具体题型估计为:
(1)题型是1个选择题或1个填空题;
(2)热点是集合的基本概念、运算和工具作用
3.集合的基本运算
(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集;
(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;
(3)能使用Venn图表达集合的关系及运算,体会直观图示对理解抽象概念的作用
2.集合间的基本关系
(1)理解集合之间包含与相等的含义,能识别给定集合的子集;
(2)在具体情境中,了解全集与空集的含义;
1.集合的含义与表示
(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;
(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com