近几年来，立体几何高考命题形式比较稳定，题目难易适中，解答题常常立足于棱柱、棱锥和正方体位置关系的证明和夹角距离的求解，而选择题、填空题又经常研究空间几何体的几何特征和体积表面积。因此复习时我们要首先掌握好空间几何体的空间结构特征。培养好空间想能力。

预测2010年高考对该讲的直接考察力度可能不大，但经常出一些创新型题目，具体预测如下：

(1)题目多出一些选择、填空题，经常出一些考察空间想象能力的试题；解答题的考察位置关系、夹角距离的载体使空间几何体，我们要想像的出其中的点线面间的位置关系；

(2)研究立体几何问题时要重视多面体的应用，才能发现隐含条件，利用隐蔽条件解题。

4．完成实习作业，如画出某些建筑的视图与直观图(在不影响图形特征的基础上，尺寸、线条等不作严格要求)；

3．通过观察用两种方法(平行投影与中心投影)画出的视图与直观图，了解空间图形的不同表示形式；

2．能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图，能识别上述的三视图所表示的立体模型，会使用材料(如：纸板)制作模型，会用斜二侧法画出它们的直观图；

1．利用实物模型、计算机软件观察大量空间图形，认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构；

5．证明两平面平行的方法：

(1)利用定义证明。利用反证法，假设两平面不平行，则它们必相交，再导出矛盾。

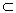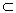(2)判定定理：一个平面内有两条相交直线都平行于另一个平面，则这两个平面平行，这个定理可简记为线面平行则面面平行。用符号表示是：a∩b，a α，b α，a∥β，b∥β，则α∥β。

(3)垂直于同一直线的两个平面平行。用符号表示是：a⊥α，a⊥β则α∥β。

(4)平行于同一个平面的两个平面平行。

两个平面平行的性质有五条：

(1)两个平面平行，其中一个平面内的任一直线必平行于另一个平面，这个定理可简记为：“面面平行，则线面平行”。用符号表示是：α∥β，a 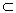α，则a∥β。

(2)如果两个平行平面同时与第三个平面相交，那么它们的交线平行，这个定理可简记为：“面面平行，则线线平行”。用符号表示是：α∥β，α∩γ=a，β∩γ=b，则a∥b。

(3)一条直线垂直于两平行平面中的一个平面,它也垂直于另一个平面。这个定理可用于证线面垂直。用符号表示是：α∥β，a⊥α，则a⊥β。

(4)夹在两个平行平面间的平行线段相等

(5)过平面外一点只有一个平面与已知平面平行

4．直线和平面相互平行

证明方法：1证明直线和这个平面内的一条直线相互平行；2证明这条直线的方向量和这个平面内的一个向量相互平行；3证明这条直线的方向量和这个平面的法向量相互垂直。

3．注意下面的转化关系：

2．注意立体几何问题向平面几何问题的转化，即立几问题平面化

在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的基础上，研究有关平行的判定依据(定义、公理和定理)、判定方法及有关性质的应用；在有关问题的解决过程中，进一步了解和掌握相关公理、定理的内容和功能，并探索立体几何中论证问题的规律；在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用．

1．用类比的思想去认识面的垂直与平行关系，注意垂直与平行间的联系。