
函数是整个高中数学的重点,其中函数思想是最重要的数学思想方法,函数问题在历年的高考中都占据相当大的比例。
从近几年来看,对本部分内容的考察形势稳中求变,向着更灵活的的方向发展,对于函数的概念及表示多以下面的形式出现:通过具体问题(几何问题、实际应用题)找出变量间的函数关系,再求出函数的定义域、值域,进而研究函数性质,寻求问题的结果。
高考对函数概念与表示考察是以选择或填空为主,以解答题形式出现的可能性相对较小,本节知识作为工具和其他知识结合起来命题的可能性依然很大
预测2010年高考对本节的考察是:
1.题型是1个选择和一个填空;
5.学会运用函数图象理解和研究函数的性质
4.通过已学过的函数特别是二次函数,理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解奇偶性的含义;
3.通过具体实例,了解简单的分段函数,并能简单应用;
2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数;
1.通过丰富实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念;
函数图象的几何特征与函数性质的数量特征紧密结合,有效地揭示了各类函数和定义域、值域、单调性、奇偶性、周期性等基本属性,体现了数形结合的特征与方法,为此,既要从定形、定性、定理、定位各方面精确地观察图形、绘制图形,又要熟练地掌握函数图象的平移变换、对称变换。
常见的函数数字特征有:
(1)函数奇偶性:
奇函数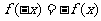 ;
;
偶函数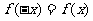 。
。
(2)函数单调性:
单调递增 或
或 ;
;
单调递增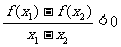 或
或 。
。
(3)函数周期性
周期为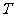 :
: 或
或 ;
;
(4)对称性
关于y轴对称: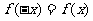 ;
;
关于原点对称: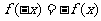 ;
;
关于直线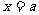 对称:
对称: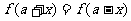 或
或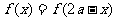 ;
;
关于点 对称:
对称: 或
或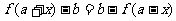 。
。
题型1:作图
例1.(08江苏理14)
设函数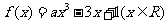 ,若对于任意的
,若对于任意的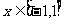 都有
都有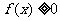 成立,则实数
成立,则实数 的值为
的值为
[解析]本小题考查函数单调性的综合运用.若x=0,则不论 取何值,
取何值,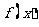 ≥0显然成立;当x>0 即
≥0显然成立;当x>0 即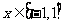 时,
时,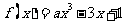 ≥0可化为,
≥0可化为,
设 ,则
,则 , 所以
, 所以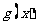 在区间
在区间 上单调递增,在区间
上单调递增,在区间 上单调递减,因此
上单调递减,因此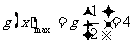 ,从而
,从而 ≥4;
≥4;
当x<0 即 时,
时,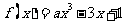 ≥0可化为
≥0可化为
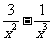 ,
,

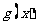 在区间
在区间 上单调递增,因此
上单调递增,因此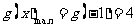 ,从而
,从而 ≤4,综上
≤4,综上 =4
=4
[答案]4
点评:该题属于实际应用的题目,结合函数值变化的趋势和一些特殊点函数值解决问题即可。要明确函数图像与函数自变量、变量值的对应关系,特别是函数单调性与函数图象个关系;
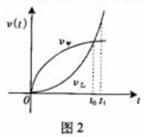
例2.(2009广东卷理)已知甲、乙两车由同一起点同时出发,并沿同一路线(假定为直线)行驶.甲车、乙车的速度曲线分别为 (如图2所示).那么对于图中给定的
(如图2所示).那么对于图中给定的 ,下列判断中一定正确的是 ( )
,下列判断中一定正确的是 ( )
 A. 在
A. 在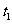 时刻,甲车在乙车前面
时刻,甲车在乙车前面
B. 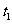 时刻后,甲车在乙车后面
时刻后,甲车在乙车后面
C. 在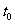 时刻,两车的位置相同
时刻,两车的位置相同
D. 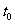 时刻后,乙车在甲车前面
时刻后,乙车在甲车前面
答案 A
解析 由图像可知,曲线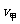 比
比 在0-
在0-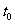 、0-
、0-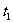 与
与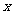 轴所围成图形面积大,则在
轴所围成图形面积大,则在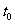 、
、 时刻,甲车均在乙车前面,选A.
时刻,甲车均在乙车前面,选A.
(2)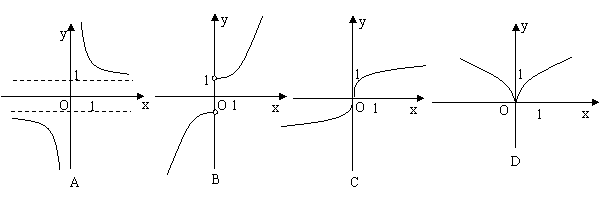 . (2009山东卷理)函数
. (2009山东卷理)函数 的图像大致为 ( ).
的图像大致为 ( ).
答案 A
解析 函数有意义,需使 ,其定义域为
,其定义域为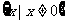 ,排除C,D,又因为
,排除C,D,又因为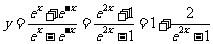 ,所以当
,所以当 时函数为减函数,故选A .
时函数为减函数,故选A .
[命题立意]:本题考查了函数的图象以及函数的定义域、值域、单调性等性质.本题的难点在于给出的函数比较复杂,需要对其先变形,再在定义域内对其进行考察其余的性质.
例3.已知函数 满足
满足 ,且当
,且当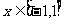 时,
时,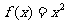 ,则
,则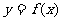 与
与 的图象的交点个数为 ( )
的图象的交点个数为 ( )
A、2 B、3 C、4 D、5
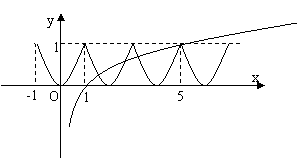 解析:由
解析:由 知函数
知函数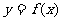 的周期为2,作出其图象如右,当x=5时,f(x)=1,log5x=1;
的周期为2,作出其图象如右,当x=5时,f(x)=1,log5x=1;
当x>5时,f(x)=1∈[0,1],
log5x>1, 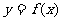 与
与 的图象不再有交点,故选C
的图象不再有交点,故选C
[巩固]设奇函数f(x)的定义域为R,且对任意实数x满足f(x+1)= -f(x),若当x∈[0,1]时,f(x)=2x-1,则f(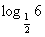 )= .
)= .
例4.(2009江西卷文)如图所示,一质点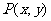 在
在 平面上沿曲线运动,
平面上沿曲线运动,
速度大小不
变,其在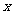 轴上的投影点
轴上的投影点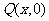 的运动速度
的运动速度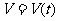 的图象
的图象
大致为 ( )

A B C D
答案 B
解析 由图可知,当质点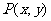 在两个封闭曲线上运动时,投影点
在两个封闭曲线上运动时,投影点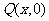 的速度先由正到0、到负数,再到0,到正,故
的速度先由正到0、到负数,再到0,到正,故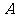 错误;质点
错误;质点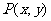 在终点的速度是由大到小接近0,故
在终点的速度是由大到小接近0,故 错误;质点
错误;质点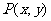 在开始时沿直线运动,故投影点
在开始时沿直线运动,故投影点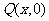 的速度为常数,因此
的速度为常数,因此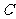 是错误的,故选
是错误的,故选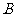 .
.
题型3:函数的图象变换
例5.(2008全国文,21)
21.(本小题满分12分)
设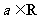 ,函数
,函数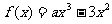 .
.
(Ⅰ)若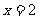 是函数
是函数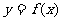 的极值点,求
的极值点,求 的值;
的值;
(Ⅱ)若函数 ,在
,在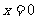 处取得最大值,求
处取得最大值,求 的取值范围.
的取值范围.
解:
(Ⅰ)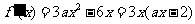 .
.
因为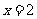 是函数
是函数 的极值点,所以
的极值点,所以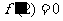 ,即
,即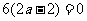 ,因此
,因此 .
.
经验证,当 时,
时,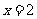 是函数
是函数 的极值点.··············································· 4分
的极值点.··············································· 4分
(Ⅱ)由题设,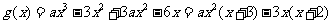 .
.
当 在区间
在区间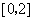 上的最大值为
上的最大值为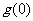 时,
时,
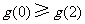 ,
,
即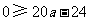 .
.
故得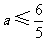 .··············································································································· 9分
.··············································································································· 9分
反之,当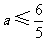 时,对任意
时,对任意 ,
,
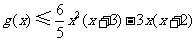
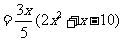
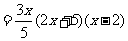
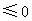 ,
,
而 ,故
,故 在区间
在区间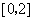 上的最大值为
上的最大值为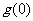 .
.
综上, 的取值范围为
的取值范围为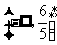 .··············································································· 12分
.··············································································· 12分
点评:借助函数图像的变换规则解决实际问题。
例6.(2009四川卷文)已知函数 是定义在实数集R上的不恒为零的偶函数,且对任意实数
是定义在实数集R上的不恒为零的偶函数,且对任意实数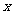 都有
都有
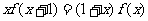 ,则
,则 的值是 ( )
的值是 ( )
A. 0 B.
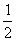 C.
1
D.
C.
1
D. 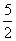
答案 A
解析 若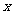 ≠0,则有
≠0,则有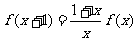 ,取
,取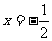 ,则有:
,则有:
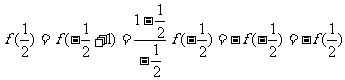 (∵
(∵ 是偶函数,则
是偶函数,则
 )由此得
)由此得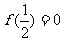 于是
于是

题型4:函数图象应用
例7.函数 与
与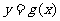 的图像如下图:则函数
的图像如下图:则函数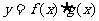 的图像可能是( )
的图像可能是( )
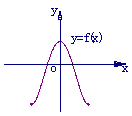

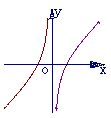

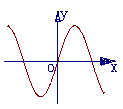


解析:∵函数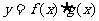 的定义域是函数
的定义域是函数 与
与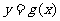 的定义域的交集
的定义域的交集 ,图像不经过坐标原点,故可以排除C、D。
,图像不经过坐标原点,故可以排除C、D。
由于当x为很小的正数时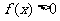 且
且 ,故
,故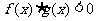 。∴选A。
。∴选A。
点评:明确函数图像在x轴上下方与函数值符号改变的关系,数值相乘“同号为正、异号为负”。
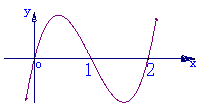 例8.已知函数f(x)=ax3+bx2+cx+d的图象如图,求b的范围。
例8.已知函数f(x)=ax3+bx2+cx+d的图象如图,求b的范围。
解法一:观察f(x)的图象,可知函数f(x)的图象过原点,即f(0)=0,得d=0,
又f(x)的图象过(1,0),
∴f(x)=a+b+c ①
又有f(-1)<0,即-a+b-c<0 ②
①+②得b<0,故b的范围是(-∞,0)
解法二:如图f(0)=0有三根0,1,2,
∴f(x)=ax3+bx2+cx+d=ax(x-1)(x-2)=ax3-3ax2+2ax,
∴b=-3a,
∵当x>2时,f(x)>0,从而有a>0,
∴b<0。
点评:通过观察函数图像,变形函数解析式,得参数的取值范围。
题型5:函数图像变换的应用
例9.已知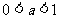 ,方程
,方程 的实根个数为( )
的实根个数为( )
A.2 B.3 C.4 D.2或3或4
根据函数与方程的关系,知方程 的根的个数即为函数
的根的个数即为函数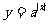 与函数
与函数 的图像交点的个数
的图像交点的个数
该题通过作图很可能选错答案为A,这是我们作图的易错点。若作图标准的话,在同一个直角坐标系下画出这两个函数的图像,由图知当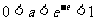 时,图像的交点个数为3个;当
时,图像的交点个数为3个;当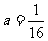 时,图像的交点个数为4个;当
时,图像的交点个数为4个;当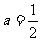 时,图像的交点个数为2个。选项为D。
时,图像的交点个数为2个。选项为D。
点评:该题属于“数形结合”的题目。解题思路是将“函数的零点”问题转化为“函数的交点问题”,借助函数的图象以及函数的图象变换规则求得结果即可。
例10.设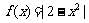 ,若
,若 ,且
,且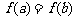 ,则
,则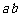 的取值范围是( )
的取值范围是( )
A.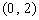 B.
B. C.
C. D.
D.
解析:保留函数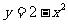 在x轴上方的图像,将其在x轴下方的图像翻折到x轴上方区即可得到函数
在x轴上方的图像,将其在x轴下方的图像翻折到x轴上方区即可得到函数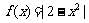 的图像
的图像
通过观察图像,可知 在区间
在区间 上是减函数,在区间
上是减函数,在区间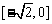 上是增函数,由
上是增函数,由 ,且
,且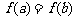 可知
可知 ,所以
,所以 ,
,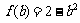 ,从而
,从而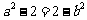 ,即
,即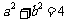 ,又
,又 ,所以
,所以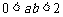 。选项为A。
。选项为A。
点评:考察函数图像的翻折变换。体现了数学由简到繁的原则,通过研究函数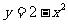 的图像和性质,进而得到
的图像和性质,进而得到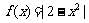 的图像和性质。
的图像和性质。
题型6:幂函数概念及性质
 例11.函数
例11.函数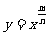
 互质)图像如图所示,则( )
互质)图像如图所示,则( )
A.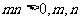 均为奇数
均为奇数
B.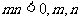 一奇一偶
一奇一偶
C.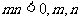 均为奇数
均为奇数
D.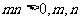 一奇一偶
一奇一偶
解析:该题考察了幂函数的性质,由于幂函数在第一象限的图像趋势表明函数在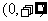 上单调递减,此时只需保证
上单调递减,此时只需保证 ,即
,即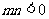 ,有
,有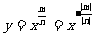 ;同时函数只在第一象限有图像,则函数的定义域为
;同时函数只在第一象限有图像,则函数的定义域为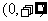 ,此时
,此时 定为偶数,
定为偶数,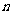 即为偶数,由于两个数互质,则
即为偶数,由于两个数互质,则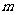 定为奇数
定为奇数
答案:选项为B。
点评:该题突破了传统借形言数思路,属于“由图形得解析式”的题目。为此需要分清幂函数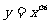 在
在 几种不同情况下函数的图像的特点,更甚至在同一种情形下
几种不同情况下函数的图像的特点,更甚至在同一种情形下 取不同数值对函数图像的影响也要了解
取不同数值对函数图像的影响也要了解
例12.画出函数的图象,试分析其性质。
解析:先要找出它是哪一种函数平移而来的,它应是由反比例函数平移而来,(这种变换是解决这类问题的关键),由此说明,是由图象向右平移3个单位,再向下平移2个单位得到的,如图所示:具体画图时对于图象与坐标轴的交点位置要大致准确,即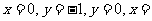 。故图象一定过(0,-1)和两个关键点。
。故图象一定过(0,-1)和两个关键点。
再观察其图象可以得到如下性质:定义域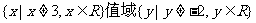 ,单调区间上单调递增;既不是奇函数也不是偶函数,但是图象是中心对称图形,对称中心是(3,-2)。
,单调区间上单调递增;既不是奇函数也不是偶函数,但是图象是中心对称图形,对称中心是(3,-2)。
点评:幂函数 的图象与性质是解决该类问题基础。注意此题两个增区间之间不能用并集号。
的图象与性质是解决该类问题基础。注意此题两个增区间之间不能用并集号。
题型7:抽象函数问题
例13.函数 的定义域为D:
的定义域为D: 且满足对于任意
且满足对于任意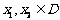 ,有
,有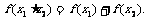
(Ⅰ)求 的值;
的值;
(Ⅱ)判断 的奇偶性并证明;
的奇偶性并证明;
(Ⅲ)如果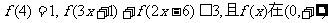 上是增函数,求x的取值范围。
上是增函数,求x的取值范围。
(Ⅰ)解:令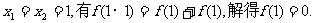
(Ⅱ)证明:令

令
∴ 为偶函数。
为偶函数。
(Ⅲ)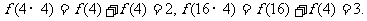
∴ (1)
(1)
∵ 上是增函数,
上是增函数,
∴(1)等价于不等式组:

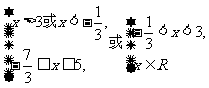
∴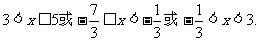
∴x的取值范 围为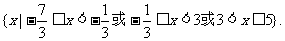
点评:以抽象函数为模型,考查函数概念,图象函数的奇偶性和周期性以及数列极限等知识,还考查运算能力和逻辑思维能力。认真分析处理好各知识的相互联系,抓住条件f(x1+x2)=f(x1)·f(x2)找到问题的突破口,由f(x1+x2)=f(x1)·f(x2)变形为 是解决问题的关键
是解决问题的关键
例14.设函数 上满足
上满足 ,且在闭区间[0,7]上,只有
,且在闭区间[0,7]上,只有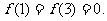
(Ⅰ)试判断函数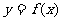 的奇偶性;
的奇偶性;
(Ⅱ)试求方程 在闭区间[-2005,2005]上的根的个数,并证明你的结论
在闭区间[-2005,2005]上的根的个数,并证明你的结论
解析:(Ⅰ)由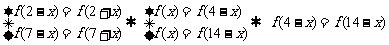
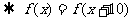 ,
,
从而知函数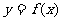 的周期为
的周期为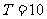
又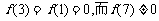 ,
,
 ,所以
,所以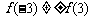
故函数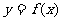 是非奇非偶函数;
是非奇非偶函数;
(II) 又
故f(x)在[0,10]和[-10,0]上均有有两个解,
从而可知函数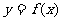 在[0,2005]上有402个解,
在[0,2005]上有402个解,
在[-2005.0]上有400个解,所以函数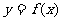 在[-2005,2005]上有802个解。
在[-2005,2005]上有802个解。
点评:充分利用函数的数字特征,并将其转化为函数的性质,再来解题。
题型8:函数图象综合问题
例15.如图,点A、B、C都在函数y=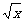 的图象上,它们的横坐标分别是a、a+1、a+2。又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)。
的图象上,它们的横坐标分别是a、a+1、a+2。又A、B、C在x轴上的射影分别是A′、B′、C′,记△AB′C的面积为f(a),△A′BC′的面积为g(a)。
(1)求函数f(a)和g(a)的表达式;
(2)比较f(a)与g(a)的大小,并证明你的结论
解: (1)连结AA′、BB′、CC′,
则f(a)=S△AB′C=S梯形AA′C′C-S△AA′B′-S△CC′B
=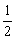 (A′A+C′C)=
(A′A+C′C)=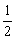 (
(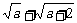 ),
),
g(a)=S△A′BC′=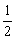 A′C′·B′B=B′B=
A′C′·B′B=B′B=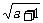 。
。
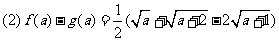
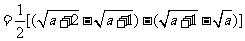

∴f(a)<g(a)。
点评:本题考查函数的解析式、函数图象、识图能力、图形的组合等,充分借助图象信息,利用面积问题的拆拼以及等价变形找到问题的突破口,解题思路:图形面积不会拆拼、数形结合、等价转化。
例16.(2008湖北理19)
如图,要设计一张矩形广告,该广告含有大小相等的左右两个矩形栏目(即图中阴影部分),这两栏的面积之和为18000cm2,四周空白的宽度为10cm,两栏之间的中缝空白的宽度为5cm,怎样确定广告的高与宽的尺寸(单位:cm),能使矩形广告面积最小?

本小题主要考查根据实际问题建立数学模型,以及运用函数、不等式等知识解决实际问题的能力.(满分12分)
解法1:设矩形栏目的高为a cm,宽为b cm,则ab=9000. ①
广告的高为a+20,宽为2b+25,其中a>0,b>0.
广告的面积S=(a+20)(2b+25)
=2ab+40b+25a+500=18500+25a+40b
≥18500+2 =18500+
=18500+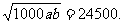
当且仅当25a=40b时等号成立,此时b= ,代入①式得a=120,从而b=75.
,代入①式得a=120,从而b=75.
即当a=120,b=75时,S取得最小值24500.
故广告的高为140 cm,宽为175 cm时,可使广告的面积最小.
解法2:设广告的高为宽分别为x
cm,y
cm,则每栏的高和宽分别为x-20, 其中x>20,y>25
其中x>20,y>25
两栏面积之和为2(x-20)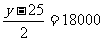 ,由此得y=
,由此得y=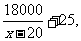
广告的面积S=xy=x(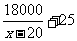 )=
)=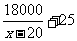 x,
x,
整理得S=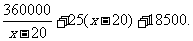
因为x-20>0,所以S≥2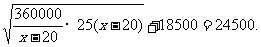
当且仅当 时等号成立,
时等号成立,
此时有(x-20)2=14400(x>20),解得x=140,代入y=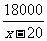 +25,得y=175,
+25,得y=175,
即当x=140,y=175时,S取得最小值24500,
故当广告的高为140 cm,宽为175 cm时,可使广告的面积最小.
点评:充分利用函数图像变换的原则,解决复合问题
2.幂函数
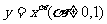 在第一象限的图象,可分为如图中的三类:
在第一象限的图象,可分为如图中的三类:
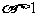

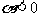
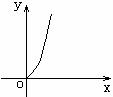
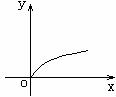
图
在考查学生对幂函数性的掌握和运用函数的性质解决问题时,所涉及的幂函数 中
中 限于在集合
限于在集合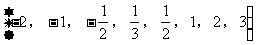 中取值
中取值
幂函数有如下性质:
⑴它的图象都过(1,1)点,都不过第四象限,且除原点外与坐标轴都不相交;
⑵定义域为R或的幂函数都具有奇偶性,定义域为 的幂函数都不具有奇偶性;
的幂函数都不具有奇偶性;
⑶幂函数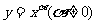 都是无界函数;在第一象限中,当
都是无界函数;在第一象限中,当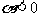 时为减函数,当
时为减函数,当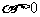 时为增函数;
时为增函数;
⑷任意两个幂函数的图象至少有一个公共点(1,1),至多有三个公共点;
1.函数图象
(1)作图方法:以解析式表示的函数作图象的方法有两种,即列表描点法和图象变换法,掌握这两种方法是本讲座的重点。
作函数图象的步骤:①确定函数的定义域;②化简函数的解析式;③讨论函数的性质即单调性、奇偶性、周期性、最值(甚至变化趋势);④描点连线,画出函数的图象。
运用描点法作图象应避免描点前的盲目性,也应避免盲目地连点成线 要把表列在关键处,要把线连在恰当处
要把表列在关键处,要把线连在恰当处 这就要求对所要画图象的存在范围、大致特征、变化趋势等作一个大概的研究。而这个研究要借助于函数性质、方程、不等式等理论和手段,是一个难点
这就要求对所要画图象的存在范围、大致特征、变化趋势等作一个大概的研究。而这个研究要借助于函数性质、方程、不等式等理论和手段,是一个难点 用图象变换法作函数图象要确定以哪一种函数的图象为基础进行变换,以及确定怎样的变换,这也是个难点
用图象变换法作函数图象要确定以哪一种函数的图象为基础进行变换,以及确定怎样的变换,这也是个难点
(2)三种图象变换:平移变换、对称变换和伸缩变换等等;
①平移变换:
Ⅰ、水平平移:函数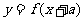 的图像可以把函数
的图像可以把函数 的图像沿
的图像沿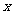 轴方向向左
轴方向向左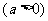 或向右
或向右 平移
平移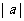 个单位即可得到;
个单位即可得到;
1)y=f(x) y=f(x+h);2)y=f(x)
y=f(x+h);2)y=f(x)  y=f(x-h);
y=f(x-h);
Ⅱ、竖直平移:函数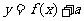 的图像可以把函数
的图像可以把函数 的图像沿
的图像沿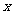 轴方向向上
轴方向向上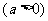 或向下
或向下 平移
平移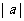 个单位即可得到;
个单位即可得到;
1)y=f(x)  y=f(x)+h;2)y=f(x)
y=f(x)+h;2)y=f(x)  y=f(x)-h
y=f(x)-h 。
。
②对称变换:
Ⅰ、函数 的图像可以将函数
的图像可以将函数 的图像关于
的图像关于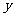 轴对称即可得到;
轴对称即可得到;
y=f(x)  y=f(-x)
y=f(-x)
Ⅱ、函数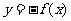 的图像可以将函数
的图像可以将函数 的图像关于
的图像关于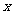 轴对称即可得到;
轴对称即可得到;
y=f(x) 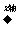 y= -f(x)
y= -f(x)
Ⅲ、函数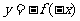 的图像可以将函数
的图像可以将函数 的图像关于原点对称即可得到;
的图像关于原点对称即可得到;
y=f(x)  y= -f(-x)
y= -f(-x)
Ⅳ、函数 的图像可以将函数
的图像可以将函数 的图像关于直线
的图像关于直线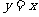 对称得到。
对称得到。
y=f(x)  x=f(y)
x=f(y)
Ⅴ、函数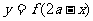 的图像可以将函数
的图像可以将函数 的图像关于直线
的图像关于直线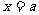 对称即可得到;
对称即可得到;
y=f(x)
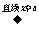 y=f(2a-x)。
y=f(2a-x)。
③翻折变换:
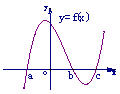
Ⅰ、函数 的图像可以将函数
的图像可以将函数 的图像的
的图像的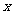 轴下方部分沿
轴下方部分沿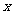 轴翻折到
轴翻折到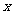 轴上方,去掉原
轴上方,去掉原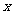 轴下方部分,并保留
轴下方部分,并保留 的
的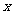 轴上方部分即可得到;
轴上方部分即可得到;
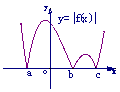
Ⅱ、函数 的图像可以将函数
的图像可以将函数 的图像右边沿
的图像右边沿 轴翻折到
轴翻折到 轴左边替代原
轴左边替代原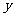 轴左边部分并保留
轴左边部分并保留 在
在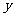 轴右边部分即可得到
轴右边部分即可得到

④伸缩变换:
Ⅰ、函数
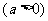 的图像可以将函数
的图像可以将函数 的图像中的每一点横坐标不变纵坐标伸长
的图像中的每一点横坐标不变纵坐标伸长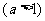 或压缩(
或压缩(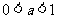 )为原来的
)为原来的 倍得到;
倍得到;
y=f(x) y=af(x)
y=af(x)
Ⅱ、函数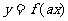
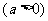 的图像可以将函数
的图像可以将函数 的图像中的每一点纵坐标不变横坐标伸长
的图像中的每一点纵坐标不变横坐标伸长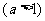 或压缩(
或压缩(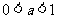 )为原来的
)为原来的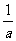 倍得到。
倍得到。
f(x) y=f(x)
y=f(x) y=f(
y=f( )
)
(3)识图:分布范围、变化趋势、对称性、周期性等等方面
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com