
1.出现1道复合其它知识的圆锥曲线综合题;
2.与圆锥曲线有关的最值问题、参数范围问题,这类问题的综合型较大,解题中需要根据具体问题、灵活运用解析几何、平面几何、函数、不等式、三角知识,正确的构造不等式或方程,体现了解析几何与其他数学知识的联系。
预测2010年高考:
近年来圆锥曲线在高考中比较稳定,解答题往往以中档题或以押轴题形式出现,主要考察学生逻辑推理能力、运算能力,考察学生综合运用数学知识解决问题的能力。但圆锥曲线在新课标中化归到选学内容,要求有所降低,估计2007年高考对本讲的考察,仍将以以下三类题型为主.
1.求曲线(或轨迹)的方程,对于这类问题,高考常常不给出图形或不给出坐标系,以考察学生理解解析几何问题的基本思想方法和能力;
3.了解圆锥曲线的简单应用.
2.通过圆锥曲线与方程的学习,进一步体会数形结合的思想;
1.由方程研究曲线,特别是圆锥曲线的几何性质问题常化为等式解决,要加强等价转化思想的训练;
3.数学思想
(1)迭加累加(等差数列的通项公式的推导方法)若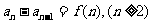 ,则……;
,则……;
(2)迭乘累乘(等比数列的通项公式的推导方法)若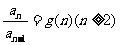 ,则……;
,则……;
(3)逆序相加(等差数列求和公式的推导方法);
(4)错位相减(等比数列求和公式的推导方法).
2.常用结论
(1) 1+2+3+...+n =
1+2+3+...+n = 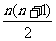
(2) 1+3+5+...+(2n-1) =
1+3+5+...+(2n-1) =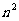
(3)
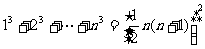
(4)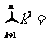
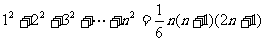
(5)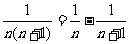
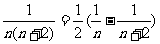
(6)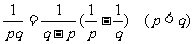
1.数列求和的常用方法
(1)公式法:适用于等差、等比数列或可转化为等差、等比数列的数列;
(2)裂项相消法:适用于 其中{
其中{ 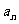 }是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等;
}是各项不为0的等差数列,c为常数;部分无理数列、含阶乘的数列等;
(3)错位相减法:适用于 其中{
其中{ 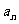 }是等差数列,
}是等差数列,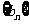 是各项不为0的等比数列。
是各项不为0的等比数列。
(4)倒序相加法:类似于等差数列前n项和公式的推导方法.
(5)分组求和法
(6)累加(乘)法等.
题型1:裂项求和
例1.已知数列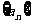 为等差数列,且公差不为0,首项也不为0,求和:
为等差数列,且公差不为0,首项也不为0,求和: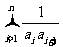 。
。
解析:首先考虑
 ,则
,则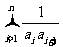 =
=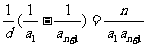 。
。
点评:已知数列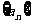 为等差数列,且公差不为0,首项也不为0,下列求和
为等差数列,且公差不为0,首项也不为0,下列求和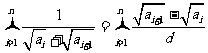 也可用裂项求和法。
也可用裂项求和法。
例2.求 。
。
解析: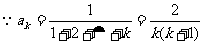 ,
,

 .
.
点评:裂项求和的关键是先将形式复杂的因式转化的简单一些。
题型2:错位相减法
例3.设a为常数,求数列a,2a2,3a3,…,nan,…的前n项和。
解析:①若a=0时,Sn=0;
②若a=1,则Sn=1+2+3+…+n=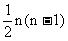 ;
;
③若a≠1,a≠0时,Sn-aSn=a(1+a+…+an-1-nan),
Sn=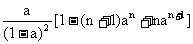 。
。
例4.已知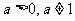 ,数列
,数列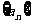 是首项为a,公比也为a的等比数列,令
是首项为a,公比也为a的等比数列,令 ,求数列
,求数列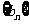 的前
的前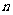 项和
项和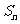 。
。
解析: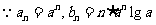 ,
,
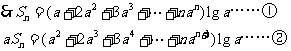

①-②得: ,
,
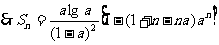 .
.
点评:设数列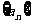 的等比数列,数列
的等比数列,数列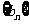 是等差数列,则数列
是等差数列,则数列 的前
的前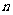 项和
项和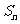 求解,均可用错位相减法。
求解,均可用错位相减法。
题型3:倒序相加
例5.求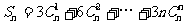 。
。
解析: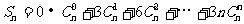 。 ①
。 ①
又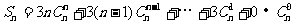 。 ②
。 ②
所以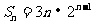 。
。
点评:Sn表示从第一项依次到第n项的和,然后又将Sn表示成第n项依次反序到第一项的和,将所得两式相加,由此得到Sn的一种求和方法。
例6.设数列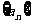 是公差为
是公差为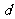 ,且首项为
,且首项为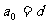 的等差数列,
的等差数列,
求和: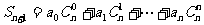
解析:因为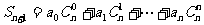 ,
,
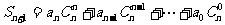
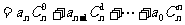 ,
,

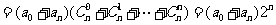
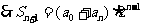 。
。
点评:此类问题还可变换为探索题形:已知数列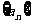 的前
的前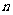 项和
项和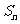
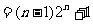 ,是否存在等差数列
,是否存在等差数列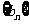 使得
使得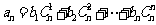 对一切自然数n都成立。
对一切自然数n都成立。
题型4:其他方法
例7.求数列1,3+5,7+9+11,13+15+17+19,…前n项和。
解析:本题实质是求一个奇数列的和。在该数列的前n项中共有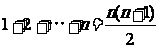 个奇数,
个奇数,
故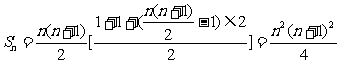 。
。
例8.求数列1,3+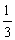 ,32+
,32+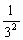 ,……,3n+
,……,3n+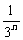 的各项的和。
的各项的和。
解析:其和为(1+3+……+3n)+(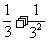 +……+
+……+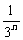 )=
)= =
=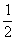 (3n+1-3-n)。
(3n+1-3-n)。
题型5:数列综合问题
例9.(2009湖北卷文)设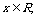 记不超过
记不超过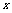 的最大整数为[
的最大整数为[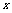 ],令{
],令{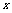 }=
}=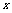 -[
-[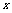 ],则{
],则{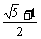 },[
},[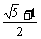 ],
],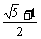
A.是等差数列但不是等比数列 B.是等比数列但不是等差数列
C.既是等差数列又是等比数列 D.既不是等差数列也不是等比数列
[答案]B
[解析]可分别求得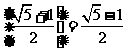 ,
, .则等比数列性质易得三者构成等比数列.
.则等比数列性质易得三者构成等比数列.
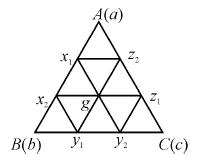
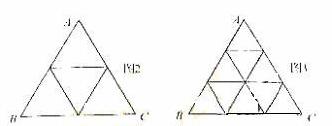
例10.(2009湖南卷理)将正⊿ABC分割成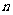
 (
(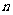 ≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)=
≥2,n∈N)个全等的小正三角形(图2,图3分别给出了n=2,3的情形),在每个三角形的顶点各放置一个数,使位于⊿ABC的三遍及平行于某边的任一直线上的数(当数的个数不少于3时)都分别一次成等差数列,若顶点A ,B ,C处的三个数互不相同且和为1,记所有顶点上的数之和为f(n),则有f(2)=2,f(3)= 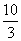 ,…,f(n)=
,…,f(n)= 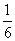 (n+1)(n+2)
(n+1)(n+2)
答案 
解析 当n=3时,如图所示分别设各顶点的数用小写字母表示,即由条件知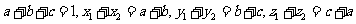


即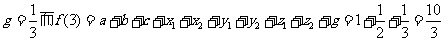
进一步可求得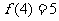 。由上知
。由上知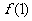 中有三个数,
中有三个数,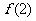 中 有6个数,
中 有6个数,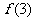 中共有10个数相加 ,
中共有10个数相加 ,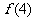 中有15个数相加….,若
中有15个数相加….,若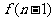 中有
中有 个数相加,可得
个数相加,可得 中有
中有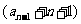 个数相加,且由
个数相加,且由
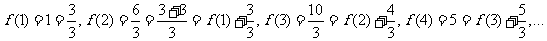
可得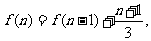 所以
所以

=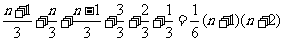
题型6:数列实际应用题
例11.某企业进行技术改造,有两种方案,甲方案:一次性贷款10万元,第一年便可获利1万元,以后每年比前一年增加30%的利润;乙方案:每年贷款1万元,第一年可获利1万元,以后每年比前一年增加5千元;两种方案的使用期都是10年,到期一次性归还本息. 若银行两种形式的贷款都按年息5%的复利计算,试比较两种方案中,哪种获利更多?
(取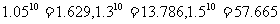 )
)
解析:甲方案是等比数列,乙方案是等差数列,
①甲方案获利: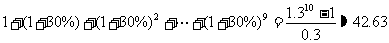 (万元),
(万元),
银行贷款本息: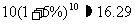 (万元),
(万元),
故甲方案纯利: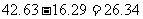 (万元),
(万元),
②乙方案获利: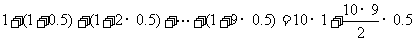
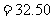 (万元);
(万元);
银行本息和: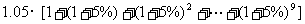
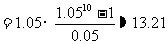 (万元)
(万元)
故乙方案纯利: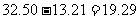 (万元);
(万元);
综上可知,甲方案更好。
点评:这是一道比较简单的数列应用问题,由于本息金与利润是熟悉的概念,因此只建立通项公式并运用所学过的公式求解.
例12.(2009年广东卷文)(本小题满分14分)
已知点(1,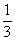 )是函数
)是函数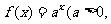 且
且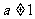 )的图象上一点,等比数列
)的图象上一点,等比数列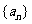 的前
的前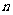 项和为
项和为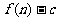 ,数列
,数列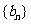
 的首项为
的首项为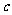 ,且前
,且前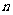 项和
项和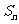 满足
满足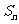 -
-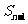 =
=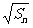 +
+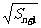 (
(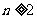 ).
).
(1)求数列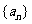 和
和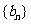 的通项公式;
的通项公式;
(2)若数列{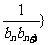 前
前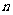 项和为
项和为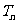 ,问
,问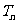 >
> 的最小正整数
的最小正整数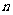 是多少?
是多少?
解(1) ,
,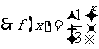
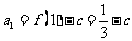 ,
,
 ,
,
 .
.
又数列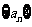 成等比数列,
成等比数列,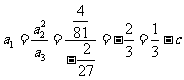 ,所以
,所以 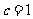 ;
;
又公比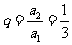 ,所以
,所以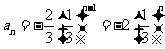
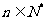 ;
;

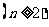
又 ,
,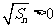 ,
, 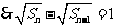 ;
;
数列 构成一个首相为1公差为1的等差数列,
构成一个首相为1公差为1的等差数列,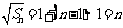 ,
, 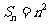
当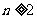 ,
, 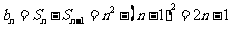 ;
;
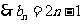 (
(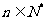 );
);
(2)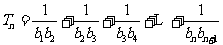
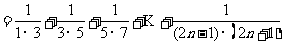
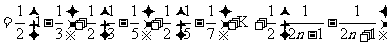
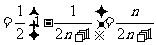 ;
;
由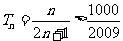 得
得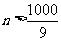 ,满足
,满足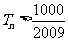 的最小正整数为112.
的最小正整数为112.
题型7:课标创新题
例13.(2009广东卷理)知曲线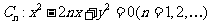 .从点
.从点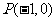 向曲线
向曲线 引斜率为
引斜率为 的切线
的切线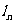 ,切点为
,切点为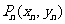 .
.
(1)求数列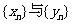 的通项公式;
的通项公式;
(2)证明: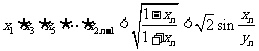 .
.
解:(1)设直线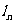 :
: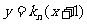 ,联立
,联立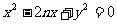 得
得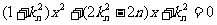 ,则
,则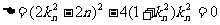 ,∴
,∴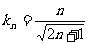 (
(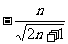 舍去)
舍去)
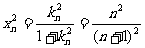 ,即
,即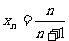 ,∴
,∴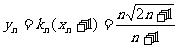
(2)证明:∵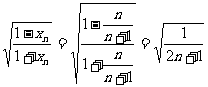
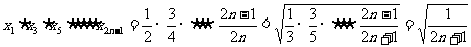
∴
由于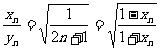 ,可令函数
,可令函数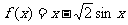 ,则
,则 ,令
,令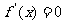 ,得
,得 ,给定区间
,给定区间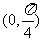 ,则有
,则有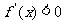 ,则函数
,则函数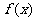 在
在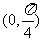 上单调递减,∴
上单调递减,∴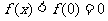 ,即
,即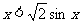 在
在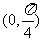 恒成立,又
恒成立,又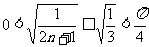 ,
,
则有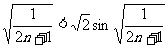 ,即
,即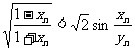 .
.
例14.(2009安徽卷理)首项为正数的数列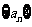 满足
满足
(I)证明:若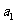 为奇数,则对一切
为奇数,则对一切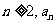 都是奇数;
都是奇数;
(II)若对一切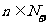 都有
都有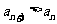 ,求
,求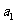 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知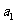 是奇数,假设
是奇数,假设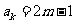 是奇数,其中
是奇数,其中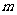 为正整数,
为正整数,
则由递推关系得 是奇数。
是奇数。
根据数学归纳法,对任何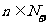 ,
,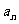 都是奇数.
都是奇数.
(II)(方法一)由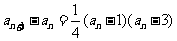 知,
知,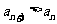 当且仅当
当且仅当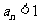 或
或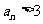 。
。
另一方面,若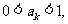 则
则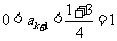 ;若
;若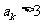 ,则
,则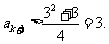
根据数学归纳法,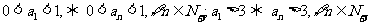
综合所述,对一切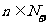 都有
都有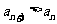 的充要条件是
的充要条件是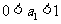 或
或 。
。
(方法二)由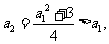 得
得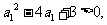 于是
于是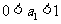 或
或 。
。
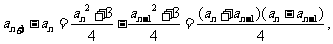
因为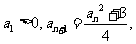 所以所有的
所以所有的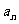 均大于0,因此
均大于0,因此 与
与 同号。
同号。
根据数学归纳法,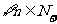 ,
, 与
与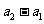 同号。
同号。
因此,对一切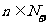 都有
都有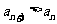 的充要条件是
的充要条件是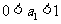 或
或 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com