
4.随机变量的均值和方差
(1)随机变量的均值
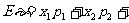 …;反映随机变量取值的平均水平.
…;反映随机变量取值的平均水平.
(2)离散型随机变量的方差:
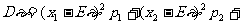 …
… …;反映随机变量取值的稳定与波动,集中与离散的程度。
…;反映随机变量取值的稳定与波动,集中与离散的程度。
基本性质: ;
;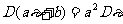 。
。
3.独立
相互独立事件:事件A(或B)是否发生对事件B(或A)发生的概率没有影响.这样的两个事件叫做相互独立事件。
独立重复试验:若n次重复试验中,每次试验结果的概率都不依赖于其他各次试验的结果,则称这n次试验是独立的.
公式
(1)两个相互独立事件同时发生的概率,等于每个事件发生的概率的积,即P(A·B)=P(A)·P(B);
推广:若事件A1,A2,…,An相互独立,则P(A1·A2…An)=P(A1)·P(A2)·…·P(n)。
(2)如果在一次试验中某事件发生的概率为P,那么在n次独立重复试验中这个事件恰好发生k次的概率:Pn(k)=C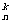 Pk(1-P)n-k。
Pk(1-P)n-k。
2.离散性随机变量的分布列
一般地,设离散型随机变量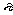 可能取得值为:
可能取得值为:
X1,X2,…,X3,…,
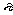 取每一个值Xi(I=1,2,…)的概率为P(
取每一个值Xi(I=1,2,…)的概率为P(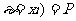 ,则称表
,则称表
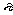 |
X1 |
X2 |
… |
xi |
… |
|
P |
P1 |
P2 |
… |
Pi |
… |
为随机变量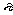 的概率分布,简称
的概率分布,简称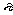 的分布列。
的分布列。
两条基本性质:①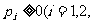 …);②P1+P2+…=1。
…);②P1+P2+…=1。
1.随机变量的概念
如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量。随机变量常用希腊字母ξ、η等表示。
对于随机变量可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量。
注:随机变量ξ是关于试验结果的函数,即每一个试验结果对应着一个实数;随机变量ξ的线性组合η=aξ+b(a、b是常数)也是随机变量。
2.卡方检验
统计中有一个有用的(读做“卡方”)统计量,它的表达式是:
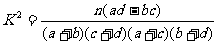 ,经过对统计量分布的研究,已经得到了两个临界值:3.841与6.635。当根据具体的数据算出的k>3.841时,有95%的把握说事件A与B有关;当k>6.635时,有99%的把握说事件A与B有关;当k
,经过对统计量分布的研究,已经得到了两个临界值:3.841与6.635。当根据具体的数据算出的k>3.841时,有95%的把握说事件A与B有关;当k>6.635时,有99%的把握说事件A与B有关;当k 3.841时,认为事件A与B是无关的。
3.841时,认为事件A与B是无关的。
随机变量
统计案例
1.相关系数
相关系数是因果统计学家皮尔逊提出的,对于变量y与x的一组观测值,把
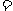


叫做变量y与x之间的样本相关系数,简称相关系数,用它来衡量两个变量之间的线性相关程度.
相关系数的性质: ≤1,且
≤1,且 越接近1,相关程度越大;且
越接近1,相关程度越大;且 越接近0,相关程度越小。
越接近0,相关程度越小。
显著性水平:显著性水平是统计假设检验中的一个概念,它是公认的小概率事件的概率值。它必须在每一次统计检验之前确定。显著性检验:(相关系数检验的步骤)由显著性水平和自由度查表得出临界值,显著性水平一般取0.01和0.05,自由度为n-2,其中n是数据的个数.在“相关系数检验的临界值表”查出与显著性水平0.05或0.01及自由度n-2(n为观测值组数)相应的相关数临界值r0.05或r0.01;例如n=7时,r0.05=0.754,r0.01=0.874 .求得的相关系数r和临界值r0.05比较,若r>r0.05,上面y与x是线性相关的,当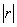 ≤r0.05或r0.01,认为线性关系不显著。
≤r0.05或r0.01,认为线性关系不显著。
结论:讨论若干变量是否线性相关,必须先进行相关性检验,在确认线性相关后,再求回归直线;

通过两个变量是否线性相关的估计,实际上就是把非确定性问题转化成确定性问题来研究; 我们研究的对象是两个变量的线性相关关系,还可以研究多个变量的相关问题,这在今后的学习中会进一步学到.
统计案例
本部分内容主要包括回归分析的基本思想及其初步应用和独立性检验的基本思想和初步应用,是教材新增内容,估计高考中比重不会过大.
预测2010年的高考主要有以下几种情况:
(1)知识点将会考察回归分析的基本思想方法,用独立性检验判断A与B间的关系,及2×2列联表;
(2)考查的形式主要以选择、填空题为主,但不会涉及很多;
随机变量的分布列
本部分内容主要包括随机变量的概念及其分布列,离散性随机变量的均值和方差,正态分布,从近几年的高考观察,这部分内容有加强命题的趋势.
预测2010年的高考对本部分内容的考查有以下情况:
(1)考查的重点将以随机变量及其分布列的概念和基本计算为主,题型以选择、填空为主,有时也以解答题形式出现;
(2)预计2010年高考还是实际情景为主,建立合适的分布列,通过均值和方差解释实际问题;
2.随机变量的分布列
(1)在对具体问题的分析中,理解取有限值的离散型随机变量及其分布列的概念,认识分布列对于刻画随机现象的重要性;
(2)通过实例(如彩票抽奖),理解超几何分布及其导出过程,并能进行简单的应用;
(3)在具体情境中,了解条件概率和两个事件相互独立的概念,理解n次独立重复试验的模型及二项分布,并能解决一些简单的实际问题;
(4)通过实例,理解取有限值的离散型随机变量均值、方差的概念,能计算简单离散型随机变量的均值、方差,并能解决一些实际问题;
(5)通过实际问题,借助直观(如实际问题的直方图),认识正态分布曲线的特点及曲线所表示的意义.
1.统计案例
通过典型案例,学习下列一些常见的统计方法,并能初步应用这些方法解决一些实际问题。
(1)通过对典型案例(如"肺癌与吸烟有关吗"等)的探究,了解独立性检验(只要求2×2列联表)的基本思想、方法及初步应用;
(2)通过对典型案例(如"质量控制"、"新药是否有效"等)的探究,了解实际推断原理和假设检验的基本思想、方法及初步应用;
(3)通过对典型案例(如"昆虫分类"等)的探究,了解聚类分析的基本思想、方法及初步应用;
(4)通过对典型案例(如"人的体重与身高的关系"等)的探究,进一步了解回归的基本思想、方法及初步应用.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com