
所以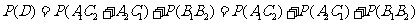
由事件的独立性的

解答2(Ⅰ)设事件A表示“一个月内被投诉2次”设事件B表示“一个月内被投诉的次数不超过1次”
所以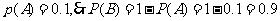
(Ⅱ)同解答1(Ⅱ)
(2008安徽理19)
(本小题满分12分)
为防止风沙危害,某地决定建设防护绿化带,种植杨树、沙柳等植物。某人一次种植了n株沙柳,各株沙柳成活与否是相互独立的,成活率为p,设 为成活沙柳的株数,数学期望
为成活沙柳的株数,数学期望 ,标准差
,标准差 为
为 。
。
(Ⅰ)求n,p的值并写出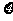 的分布列;
的分布列;
(Ⅱ)若有3株或3株以上的沙柳未成活,则需要补种,求需要补种沙柳的概率
(1)由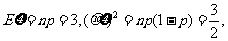 得
得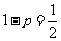 ,从而
,从而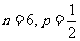
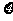 的分布列为
的分布列为
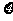 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
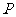 |
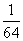 |
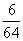 |
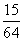 |
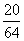 |
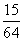 |
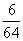 |
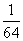 |
(2)记”需要补种沙柳”为事件A, 则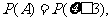 得
得
 或
或 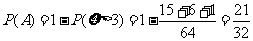
题型1:随机事件的定义
例1.判断下列事件哪些是必然事件,哪些是不可能事件,哪些是随机事件?
(1)“抛一石块,下落”.
(2)“在标准大气压下且温度低于0℃时,冰融化”;
(3)“某人射击一次,中靶”;
(4)“如果a>b,那么a-b>0”;
(5)“掷一枚硬币,出现正面”;
(6)“导体通电后,发热”;
(7)“从分别标有号数1,2,3,4,5的5张标签中任取一张,得到4号签”;
(8)“某电话机在1分钟内收到2次呼叫”;
(9)“没有水份,种子能发芽”;
(10)“在常温下,焊锡熔化”.
解析:根据定义,事件(1)、(4)、(6)是必然事件;事件(2)、(9)、(10)是不可能事件;事件(3)、(5)、(7)、(8)是随机事件.
点评:熟悉必然事件、不可能事件、随机事件的联系与区别。针对不同的问题加以区分。
例2.(1)如果某种彩票中奖的概率为 ,那么买1000张彩票一定能中奖吗?请用概率的意义解释。
,那么买1000张彩票一定能中奖吗?请用概率的意义解释。
解析:不一定能中奖,因为,买1000张彩票相当于做1000次试验,因为每次试验的结果都是随机的,即每张彩票可能中奖也可能不中奖,因此,1000张彩票中可能没有一张中奖,也可能有一张、两张乃至多张中奖。
点评:买1000张彩票,相当于1000次试验,因为每次试验的结果都是随机的,所以做1000次试验的结果也是随机的,也就是说,买1000张彩票有可能没有一张中奖。
(2)在一场乒乓球比赛前,裁判员利用抽签器来决定由谁先发球,请用概率的知识解释其公平性。
解析:这个规则是公平的,因为抽签上抛后,红圈朝上与绿圈朝上的概率均是0.5,因此任何一名运动员猜中的概率都是0.5,也就是每个运动员取得先发球权的概率都是0.5。
点评:这个规则是公平的,因为每个运动员先发球的概率为0.5,即每个运动员取得先发球权的概率是0.5。事实上,只能使两个运动员取得先发球权的概率都是0.5的规则都是公平的.
题型2:频率与概率
例3.某种菜籽在相同在相同的条件下发芽试验结果如下表:(求其发芽的概率)
|
种子粒数 |
2 |
5 |
10 |
70 |
130 |
310 |
700 |
1500 |
2000 |
3000 |
|
发芽粒数 |
2 |
4 |
9 |
60 |
116 |
282 |
639 |
1339 |
1806 |
2715 |
解析:我们根据表格只能计算不同情况下的种子发芽的频率分别是:1,0.8,0.9,0.857,0.892,0.910,0.913,0.893,0.903,0.905。随着种子粒数的增加,菜籽发芽的频率越接近于0.9,且在它附近摆动。故此种子发芽的概率为0.9。
点评:我们可以用频率的趋向近似值表示随机事件发生的概率.
例4.进行这样的试验:从0、1、2、…、9这十个数字中随机取一个数字,重复进行这个试验10000次,将每次取得的数字依次记下来,我们就得到一个包括10000个数字的“随机数表”.在这个随机数表里,可以发现0、1、2、…、9这十个数字中各个数字出现的频率稳定在0.1附近.现在我们把一个随机数表等分为10段,每段包括1000个随机数,统计每1000个随机数中数字“7”出现的频率,得到如下的结果:
|
段序:n=1000 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
出现“7”的频数 |
95 |
88 |
95 |
112 |
95 |
99 |
82 |
89 |
111 |
102 |
|
出现“7”的频率 |
0.095 |
0.088 |
0.095 |
0.112 |
0.095 |
0.099 |
0.082 |
0.089 |
0.111 |
0.102 |
由上表可见,每1000个随机数中“7”出现的频率也稳定在0.1的附近.这就是频率的稳定性.我们把随机事件A的频率P(A)作为随机事件A的概率P(A)的近似值。
点评:利用概率的统计定义,在计算每一个随机事件概率时都要通过大量重复的试验,列出一个表格,从表格中找到某事件出现频率的近似值作为所求概率。这从某种意义上说是很繁琐的.
题型3:随机事件间的关系
例5.(2009江西卷文)甲、乙、丙、丁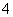 个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这
个足球队参加比赛,假设每场比赛各队取胜的概率相等,现任意将这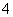 个队分成两个组(每组两个队)进行比赛,胜者再赛,则甲、乙相遇的概率为 ( )
个队分成两个组(每组两个队)进行比赛,胜者再赛,则甲、乙相遇的概率为 ( )
A.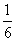 B.
B.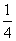 C.
C.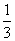 D.
D.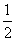

[解析]所有可能的比赛分组情况共有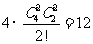 种,甲乙相遇的分组情况恰好有6种,故选
种,甲乙相遇的分组情况恰好有6种,故选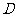 .
. 
答案 D
(1)(2009江苏卷)现有5根竹竿,它们的长度(单位:m)分别为2.5,2.6,2.7,2.8,2.9,若从中一次随机抽取2根竹竿,则它们的长度恰好相差0.3m的概率为 . 
[解析] 考查等可能事件的概率知识。 
从5根竹竿中一次随机抽取2根的可能的事件总数为10,它们的长度恰好相差0.3m的事件数为2,分别是:2.5和2.8,2.6和2.9,所求概率为0.2。
答案 0.2
(2)把标号为1,2,3,4的四个小球随机地分发给甲、乙、丙、丁四个人,每人分得一个。事件“甲分得1号球”与事件“乙分得1号球”是(
)
(A)互斥但非对立事件 (B)对立事件
(C)相互独立事件
(D)以上都不对
答案:A。
点评:一定要区分开对立和互斥的定义,互斥事件:不能同时发生的两个事件叫做互斥事件;对立事件:不能同时发生,但必有一个发生的两个事件叫做互斥事件。
例6.15.(2009湖北卷文)甲、乙、丙三人将参加某项测试,他们能达标的概率分别是0.8、0.6、
0.5,则三人都达标的概率是
,三人中至少有一人达标的概率是
。
[解析]三人均达标为0.8×0.6×0.5=0.24,三人中至少有一人达标为1-0.24=0.76
答案 0.24 0.76
点评:本小题考查互斥事件、相互独立事件的概率等基础知识,及分析和解决实际问题的能力。
题型4:古典概率模型的计算问题
例7.从含有两件正品a1,a2和一件次品b1的三件产品中,每次任取一件,每次取出后不放回,连续取两次,求取出的两件产品中恰有一件次品的概率.
解析:每次取出一个,取后不放回地连续取两次,其一切可能的结果组成的基本事件有6个,即(a1,a2)和,(a1,b2),(a2,a1),(a2,b1),(b1,a1),(b2,a2)。其中小括号内左边的字母表示第1次取出的产品,右边的字母表示第2次取出的产用A表示“取出的两种中,恰好有一件次品”这一事件,
则A=[(a1,b1),(a2,b1),(b1,a1),(b1,a2)],
事件A由4个基本事件组成,因而,P(A)=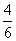 =
=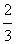 。
。
点评:利用古典概型的计算公式时应注意两点:(1)所有的基本事件必须是互斥的;(2)m为事件A所包含的基本事件数,求m值时,要做到不重不漏.
例8.现有一批产品共有10件,其中8件为正品,2件为次品:
(1)如果从中取出一件,然后放回,再取一件,求连续3次取出的都是正品的概率;
(2)如果从中一次取3件,求3件都是正品的概率。
分析:(1)为返回抽样;(2)为不返回抽样.
解析:(1)有放回地抽取3次,按抽取顺序(x,y,z)记录结果,则x,y,z都有10种可能,所以试验结果有10×10×10=103种;设事件A为“连续3次都取正品”,则包含的基本事件共有8×8×8=83种,因此,P(A)= 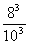 =0.512。
=0.512。
(2)解法1:可以看作不放回抽样3次,顺序不同,基本事件不同,按抽取顺序记录(x,y,z),则x有10种可能,y有9种可能,z有8种可能,所以试验的所有结果为10×9×8=720种.设事件B为“3件都是正品”,则事件B包含的基本事件总数为8×7×6=336, 所以P(B)= 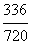 ≈0.467。
≈0.467。
解法2:可以看作不放回3次无顺序抽样,先按抽取顺序(x,y,z)记录结果,则x有10种可能,y有9种可能,z有8种可能,但(x,y,z),(x,z,y),(y,x,z),(y,z,x),(z,x,y),(z,y,x),是相同的,所以试验的所有结果有10×9×8÷6=120,按同样的方法,事件B包含的基本事件个数为8×7×6÷6=56,因此P(B)= 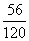 ≈0.467。
≈0.467。
点评:关于不放回抽样,计算基本事件个数时,既可以看作是有顺序的,也可以看作是无顺序的,其结果是一样的,但不论选择哪一种方式,观察的角度必须一致,否则会导致错误.
题型5:利用排列组合知识解古典概型问题
例9.(2008四川理)
从甲、乙等10个同学中挑选4名参加某项公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有( C )
(A)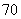 种 (B)
种 (B) 种 (C)
种 (C)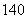 种 (D)
种 (D)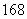 种
种
[解]:∵从10个同学中挑选4名参加某项公益活动有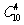 种不同挑选方法;
种不同挑选方法;
从甲、乙之外的8个同学中挑选4名参加某项公益活动有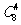 种不同挑选方法;
种不同挑选方法;
∴甲、乙中至少有1人参加,则不同的挑选方法共有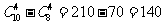 种不同挑选方法 故选C;
种不同挑选方法 故选C;
[考点]:此题重点考察组合的意义和组合数公式;
[突破]:从参加 “某项”切入,选中的无区别,从而为组合问题;由“至少”从反面排除易于解决;
点评:该题通过排列、组合知识完成了古典概型的计算问题,同时要做到所有的基本事件必须是互斥的,要做到不重不漏。
例10.在添加剂的搭配使用中,为了找到最佳的搭配方案,需要对各种不同的搭配方式作比较。在试制某种牙膏新品种时,需要选用两种不同的添加剂。现有芳香度分别为0,1,2,3,4,5的六种添加剂可供选用。根据试验设计原理,通常首先要随机选取两种不同的添加剂进行搭配试验.
(Ⅰ)求所选用的两种不同的添加剂的芳香度之和等于4的概率;
(Ⅱ)求所选用的两种不同的添加剂的芳香度之和不小于3的概率;
解析:设“所选用的两种不同的添加剂的芳香度之和等于4”的事件为A,“所选用的两种不同的添加剂的芳香度之和不小于3”的事件为B
(Ⅰ)芳香度之和等于4的取法有2种: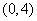 、
、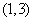 ,故
,故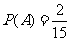 。
。
(Ⅱ)芳香度之和等于1的取法有1种: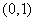 ;芳香度之和等于2的取法有1种:
;芳香度之和等于2的取法有1种: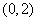 ,故
,故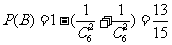 。
。
点评:高考对概率内容的考查,往往以实际应用题出现。这既是这类问题的特点,也符合高考发展方向,考生要以课本概念和方法为主,以熟练技能,巩固概念为目标,查找知识缺漏,总结解题规律.
题型6:易错题辨析
例11.掷两枚骰子,求所得的点数之和为6的概率.
错解:掷两枚骰子出现的点数之和不同情况为{2,3,4,…,12},故共有11种基本事件,所以概率为P=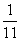 ;
;
剖析:以上11种基本事件不是等可能的,如点数和2只有(1,1),而点数之和为6有(1,5)、(2,4)、(3,3)、(4,2)、(5,1)共5种.事实上,掷两枚骰子共有36种基本事件,且是等可能的,所以“所得点数之和为6”的概率为P=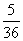 。
。
我们经常见的错里还有“投掷两枚硬币的结果”,划分基本事件“两正、一正一反、两反”,其中“一正一反”与“两正”、“两反”的机会是不均等.
类型四:基本事件 “不可数”
由概率求值公式 ,求某一事件发生的概率时,要求试验中所有可能出现的基本事件只有有限个.
,求某一事件发生的概率时,要求试验中所有可能出现的基本事件只有有限个.
如果试验所包含的基本事件是无限多个,那根本就不会得到基本事件的总数,也就不能用 公式来解决问题.
公式来解决问题.
例12.
甲、乙二人参加普法知识竞赛,共有10个不同的题目,其中选择题6个,判断题4个,甲、乙二人一次各抽取一题,
(1)甲抽到选择题,乙抽到判断题的概率是多少?
错解:甲从选择题中抽到一题的可能结果有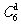 个,乙从判断题中抽到一题的的可能结果是
个,乙从判断题中抽到一题的的可能结果是 ,故甲抽到选择题,乙抽到判断题的可能结果为
,故甲抽到选择题,乙抽到判断题的可能结果为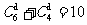 ;又甲、乙二人一次各抽取一题的结果有
;又甲、乙二人一次各抽取一题的结果有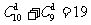 ,所以概率值为
,所以概率值为 。
。
剖析:错把分步原理当作分类原理来处理。
正解:甲从选择题中抽到一题的可能结果有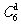 个,乙从判断题中抽到一题的的可能结果是
个,乙从判断题中抽到一题的的可能结果是 ,故甲抽到选择题,乙抽到判断题的可能结果为
,故甲抽到选择题,乙抽到判断题的可能结果为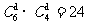 ;又甲、乙二人一次各抽取一题的结果有
;又甲、乙二人一次各抽取一题的结果有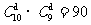 ,所以概率值为
,所以概率值为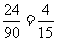 。
。
(2)甲、乙二人至少有一个抽到选择题的概率是多少?
错解:甲、乙中甲抽到判断题的种数是6×9种,乙抽到判断题的种数6×9种,故甲、乙二人至少有一个抽到选择题的种数为12×9;又甲、乙二人一次各抽取一题的种数是10×9,故甲、乙二人至少有一个抽到选择题的概率是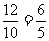 。
。
剖析:显然概率值不会大于1,这是错解。该问题对甲、乙二人至少有一个抽到选择题的计数是重复的,两人都抽取到选择题这种情况被重复计数.
正解:甲、乙二人一次各抽取一题基本事件的总数是10×9=90;
方法一:分类计数原理
(1)只有甲抽到了选择题的事件数是:6×4=24;
(2)只有乙抽到了选择题的事件数是:6×4=24;
(3)甲、乙同时抽到选择题的事件数是:6×5=30;
故甲、乙二人至少有一个抽到选择题的概率是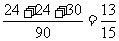 。
。
方法二:利用对立事件
事件“甲、乙二人至少有一个抽到选择题”与事件“甲、乙两人都未抽到选择题”是对立事件.
事件“甲、乙两人都未抽到选择题”的基本事件个数是4×3=12;
故甲、乙二人至少有一个抽到选择题的概率是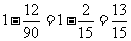 。
。
例14(2009陕西卷文)(本小题满分12分)
椐统计,某食品企业一个月内被消费者投诉的次数为0,1,2的概率分别为0.4,0.5,0.1
(Ⅰ) 求该企业在一个月内共被消费者投诉不超过1次的概率;
(Ⅱ)假设一月份与二月份被消费者投诉的次数互不影响,求该企业在这两个月内共被消费者投诉2次的概率.
解 解答1(Ⅰ)设事件A表示“一个月内被投诉的次数为0”事件B表示“一个月内被投诉的次数为1”
所以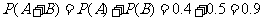
(Ⅱ)设事件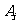 表示“第
表示“第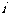 个月被投诉的次数为0”事件
个月被投诉的次数为0”事件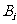 表示“第
表示“第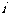 个月被投诉的次数为1”事件
个月被投诉的次数为1”事件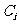 表示“第
表示“第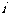 个月被投诉的次数为2”事件D表示“两个月内被投诉2次”
个月被投诉的次数为2”事件D表示“两个月内被投诉2次”
所以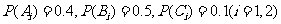
所以两个月中,一个月被投诉2次,另一个月被投诉0次的概率为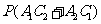
5.古典概型
(1)古典概型的两大特点:1)试验中所有可能出现的基本事件只有有限个;2)每个基本事件出现的可能性相等;
(2)古典概型的概率计算公式:P(A)= ;
;
一次试验连同其中可能出现的每一个结果称为一个基本事件,通常此试验中的某一事件A由几个基本事件组成.如果一次试验中可能出现的结果有n个,即此试验由n个基本事件组成,而且所有结果出现的可能性都相等,那么每一基本事件的概率都是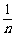 。如果某个事件A包含的结果有m个,那么事件A的概率P(A)=
。如果某个事件A包含的结果有m个,那么事件A的概率P(A)=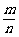 。
。
4.事件间的运算
(1)并事件(和事件)
若某事件的发生是事件A发生或事件B发生,则此事件称为事件A与事件B的并事件。
注:当A和B互斥时,事件A+B的概率满足加法公式:
P(A+B)=P(A)+P(B)(A、B互斥);且有P(A+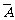 )=P(A)+P(
)=P(A)+P(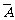 )=1。
)=1。
(2)交事件(积事件)
若某事件的发生是事件A发生和事件B同时发生,则此事件称为事件A与事件B的交事件.
3.事件间的关系
(1)互斥事件:不能同时发生的两个事件叫做互斥事件;
(2)对立事件:不能同时发生,但必有一个发生的两个事件叫做互斥事件;
(3)包含:事件A发生时事件B一定发生,称事件A包含于事件B(或事件B包含事件A);
2.随机事件的概率
事件A的概率:在大量重复进行同一试验时,事件A发生的频率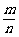 总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A)。
总接近于某个常数,在它附近摆动,这时就把这个常数叫做事件A的概率,记作P(A)。
由定义可知0≤P(A)≤1,显然必然事件的概率是1,不可能事件的概率是0。
1.随机事件的概念
在一定的条件下所出现的某种结果叫做事件。
(1)随机事件:在一定条件下可能发生也可能不发生的事件;
(2)必然事件:在一定条件下必然要发生的事件;
(3)不可能事件:在一定条件下不可能发生的事件.
本讲内容在高考中所占比重不大,纵贯近几年的高考形式对涉及到有关概念的某些计算要求降低,但试题中具有一定的灵活性、机动性.
预测2010年高考:
(1)对于理科生来讲,对随机事件的考察,结合选修中排列、组合的知识进行考察,多以选择题、填空题形式出现;
(2)对概率考察的重点为互斥事件、古典概型的概率事件的计算为主,而以实际应用题出现的形式多以选择题、填空题为主.
3.通过实例,理解古典概型及其概率计算公式,会用列举法计算一些随机事件所含的基本事件数及事件发生的概率。
2.通过实例,了解两个互斥事件的概率加法公式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com