三种常用抽样方法：

1．简单随机抽样：设一个总体的个数为N。如果通过逐个抽取的方法从中抽取一个样本，且每次抽取时各个个体被抽到的概率相等，就称这样的抽样为简单随机抽样。实现简单随机抽样，常用抽签法和随机数表法.

(1)抽签法

制签：先将总体中的所有个体编号(号码可以从1到N)，并把号码写在形状、大小相同的号签上，号签可以用小球、卡片、纸条等制作，然后将这些号签放在同一个箱子里，进行均匀搅拌；

抽签：抽签时，每次从中抽出1个号签，连续抽取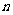次；

成样：对应号签就得到一个容量为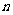的样本。

抽签法简便易行，当总体的个体数不多时，适宜采用这种方法.

(2)随机数表法

编号：对总体进行编号，保证位数一致；

数数：当随机地选定开始读数的数后，读数的方向可以向右，也可以向左、向上、向下等等。在读数过程中，得到一串数字号码，在去掉其中不合要求和与前面重复的号码后，其中依次出现的号码可以看成是依次从总体中抽取的各个个体的号码。

成样：对应号签就得到一个容量为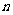的样本.

结论：

　 ① 用简单随机抽样，从含有N个个体的总体中抽取一个容量为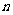的样本时，每次抽取一个个体时任一个体被抽到的概率为；在整个抽样过程中各个个体被抽到的概率为；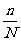

② 基于此，简单随机抽样体现了抽样的客观性与公平性；

③ 简单随机抽样的特点：它是不放回抽样；它是逐个地进行抽取；它是一种等概率抽样。

统计是在初中数学统计初步的深化和扩展，本讲的主要内容是随机抽样的方法在总体中抽取样本。

预测2010年高考对本讲的考察是：

(1)以基本题(中、低档题为主)，多以选择题、填空题的形式出现，以实际问题为背景，综合考察学生学习基础的知识、应用基础知识、解决实际问题的能力；

(2)热点是随机抽样方法中的分层抽样、系统抽样方法.

4．能通过试验、查阅资料、设计调查问卷等方法收集数据.

3．在参与解决统计问题的过程中，学会用简单随机抽样方法从总体中抽取样本；通过对实例的分析，了解分层抽样和系统抽样方法；

2．结合具体的实际问题情境，理解随机抽样的必要性和重要性；

1．能从现实生活或其他学科中提出具有一定价值的统计问题；

4．在应用题背景条件下，能否把一个复杂事件分解为若干个互相排斥或相互独立、既不重复又不遗漏的简单事件是解答这类应用题的关键，也是考查学生分析问题、解决问题的能力的重要环节.

3．对立事件是互斥事件的一种特殊情况，是指在一次试验中有且仅有一个发生的两个事件，集合A的对立事件记作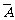，从集合的角度来看，事件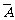所含结果的集合正是全集U中由事件A所含结果组成集合的补集，即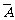A∪=U，A∩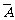=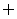.对立事件一定是互斥事件，但互斥事件不一定是对立事件。

事件A、B的和记作A+B，表示事件A、B至少有一个发生。当A、B为互斥事件时，事件A+B是由“A发生而B不发生”以及“B发生而A不发生”构成的。

当计算事件A的概率P(A)比较困难时，有时计算它的对立事件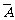的概率则要容易些，为此有P(A)=1－P()。

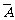对于n个互斥事件A₁，A₂，…，A_n，其加法公式为P(A₁+A₂+…+A_n)=P(A₁)+P(A₂)+…+P(A_n)。

分类讨论思想是解决互斥事件有一个发生的概率的一个重要的指导思想。

2．对于互斥事件要抓住如下的特征进行理解：

第一，互斥事件研究的是两个事件之间的关系；

第二，所研究的两个事件是在一次试验中涉及的；

第三，两个事件互斥是从试验的结果不能同时出现来确定的.

本讲概念性强、抽象性强、思维方法独特。因此要立足于基础知识、基本方法、基本问题的练习，恰当选取典型例题，构建思维模式，造就思维依托和思维的合理定势.

1．使用公式P(A)=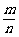计算时，确定m、n的数值是关键所在,其计算方法灵活多变,没有固定的模式，可充分利用排列组合知识中的分类计数原理和分步计数原理，必须做到不重复不遗漏.

复习这部分内容及解答此类问题首先必须使学生明确判断两点：(1)对于每个随机实验来说，所有可能出现的实验结果数n必须是有限个；(2)出现的所有不同的实验结果数m其可能性大小必须是相同的。只有在同时满足(1)、(2)的条件下，运用的古典概型计算公式P(A)=m/n得出的结果才是正确的。