
0.02mol 0.02mol
根据反应耗用盐酸的量列方程求解
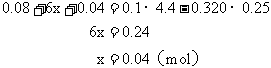
Fe2O3的质量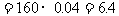 (g)
(g)
Fe的质量 (g)
(g)
答案:Fe的质量为5.6g; CuO的质量为1.6g; Fe2O3的质量为6.4g。
[例5]已知NO2与NaOH溶液反应:
3NO2+2NaOH=2NaNO3+NO+H2O,NO和NO2可一起与NaOH溶液作用
NO2+NO+2NaOH= 2NaNO2+H2O现欲用V L某烧碱溶液使由nmol NO和m mol NO2组成的混合气体中的氮全部进入溶液中,NaOH溶液的物质的量浓度至少为多少?
解析:NO和NO2的混合气体与NaOH溶液反应,产物为NaNO2,产物中Na+与NO2-的物质的量比为1∶1,根据反应中Na+与N原子的物质的量守恒,可列出方程。
设NaOH溶液的物质的量浓度为x。
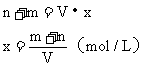
答案:(m+n)/v
[例6]把2.56g纯铜放入盛有一定量浓HNO3的大试管中,立即发生化学反应,当铜反应完毕后,共生成气体1.12L(标况),计算此反应中耗用HNO3的物质的量是多少?
解析:铜跟一定量浓HNO3反应,开始生成的还原产物是NO2,后期生成的还原产物是NO,把两个不同反应所生成的还原产物作为整体考虑,而不区分有多少NO2和NO,每生成1mol NOx都耗用1mol HNO3,根据以应前后氮原子守恒,可列方程求解

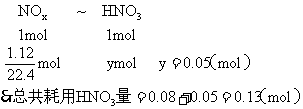
答案:0.13 moL
[例7]将7.28g Fe溶于过量的稀H2SO4中,在加热的条件下,用2.02gKNO3去氧化溶液中Fe2+,待反应完全后,剩余Fe2+还需0.4mol/L KMnO4溶液25mL才能完全氧化,已知其反应方程式为:5Fe2++MnO4-+8H+=Mn2++5 Fe3++4H2O。通过计算、确定KNO3的还原产物是什么?(还原产物为氧化物)并写出其离子方程式。
解析:该题中Fe已全部被转化为Fe2+,因此Fe2+与KNO3、KMnO4的氧化还原反应中,还原剂为Fe2+,氧化剂为KNO3、KMnO4,根据电子得失守恒列方程。
Fe2+失去电子的物质的量= KMnO4得到电子的物质的量+KNO3得到电子的物质的量

离子方程式:2 NO3-+8 Fe2++10H+=N2O+8 Fe3++5H2O
答案:KNO3的还原产物是N2O 离子方程式:2 NO3-+8 Fe2++10H+=N2O+8 Fe3++5H2O
[例8]镁条在空气中燃烧生成氧化镁和氮化镁。将燃烧后的产物溶解在60毫升浓度为2.0mol/升的盐酸中,再用20毫升0.5mol/升NaOH溶液中和多余的盐酸,然后在此溶液中加过量的碱,把氨全部蒸出来,用稀HCl吸收,稀HCl增重0.17g,求镁带的质量。
解析:此题涉及反应较多,如按常规计算非常复杂,如巧用电荷守恒法可使计算大为简化。
该题反应变化的图式:

在图(B)中,根据电荷守恒,有下列关系:
2n(Mg2+) + n(NH4+) + n(Na+) = n(Cl-)
把数据代入 解得n(Mg2+) =0.05moL
则镁带的质量=1.2g
答案:镁带的质量为1.2g
2.守恒法的最基本原理为-----质量守恒定律,并由此衍生出来:
一切化学变化中都存在的-----微粒守恒
氧化还原反应中存在的-----得失电子守恒
化合物的化学式存在的-----正、负化合价总数相等
电解质溶液中存在的-----阴、阳离子电荷守恒
试题枚举
[例1]例题5某烃0.1mol,与在标准状况下为20 L的氧气(过量)充分反应后,迅速将混合气体通入足量Na2O2粉末中,在一定设备中使气体完全反应,此时粉末增重15 g。经处理后得到气体14.4 L(标准状况)。该烃能使溴水褪色,试通过计算求出该烃的分子式,并写出可能的结构简式。
解析:设该烃的分子量为M
经分析可推断14.4 L气体均为氧气。根据质量守恒:
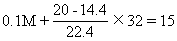
解得M=70 由估算法70/12=5 余10
所以该烃化学式为C5H10。因为该烃能使溴水褪色,故为烯烃。戊烯共有5种可能的结构简式:①CH2=CH-CH2-CH2-CH3
②CH3-CH=CH-CH2-CH3
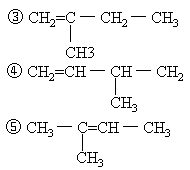
[例2]酸雨是因为过度燃烧煤和石油,生成的硫的氧化物与氮的氧化物溶于水生成硫酸和硝酸的缘故。某次雨水的分析数据如下:
c(NH4+)=2.0×10-6mol/L c(Cl-)=6.0×10-6mol/L
c(Na+)=3.0×10-6mol/L c(NO3-)=2.3×10-5mol/L
c(SO42-)=2.8×10-5mol/L
则此次雨水的pH大约为 ( )
A.3 B.4 C.5 D.6
解析:此题应根据雨水中阴、阳离子所带负、正电荷守恒(溶液呈电中性)解析,根据电荷守恒:
c(H+)+ c(NH4+)+ c(Na+)= c(Cl-)+ c(NO3-)+2 c(SO42-)
计算出c(H+) 再代入pH=-lg c(H+) =5-lg8≈4
答案:B。
[例3]在30mL量筒中充满NO2和O2的混合气体,倒立于水中使气体充分反应,最后剩余5mL气体,求原混合气中氧气的体积是多少毫升?
解析:解法(一)
设原混合气中氧气的体积为y(mL)
(1)设O2过量:根据4NO2+O2+2H2O=4HNO3,则O2得电子数等于NO2失电子数。
(y-5)×4=(30-y)×1
解得y=10(mL)
(2)若NO2过量:
4NO2+O2+2H2O=4HNO3
4y y
3NO2+H2O=2HNO3+NO
5
因为在全部(30-y)mLNO2中,有5mLNO2得电子转变为NO,其余(30-y-5)mLNO2都失电子转变为HNO3。
O2得电子数(NO2→NO)时得电子数等于(NO2→HNO3)时失电子数。
解法(二)根据得失电子守恒,利用阿伏加德罗定律转化信息,将体积数转化为物质的量简化计算。凡氧化还原反应,一般均可利用电子得失守恒法进行计算。
4y+5×2=(30-y-5)×1
解得y=3(mL)
答案:原氧气体积可能为10mL或3mL
[例4]将Wg铁、氧化铁和氧化铜组成的混合物粉未放入100mL 4.4mol/L盐酸中,反应完全后得氢气896mL(标况),生成的溶液中只有FeCl2、HCl和1.28g固体。把溶液稀释到320mL时,盐酸的物质的量浓度为0.25mol/L,求混合物中各物质是多少g?
解析:解答此题的关键,是审清题意,找出等量关系,选准突破口。首先确定由生成溶液中的盐酸可知反应后的1.28g固体沉淀物为铜,因此可首先确定CuO的质量。再根据各反应化学方程式中诸物质的量的关系和耗用盐酸的物质的量列方程求解,或寻求题中“隐含”的电子守恒和Cl-守恒条件,求得Fe和Fe2O3的质量。
Cu的物质的量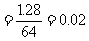 mol
mol
CuO的质量=0.02×80=1.6(g)
设混合物中Fe2O3的物质的量为x。
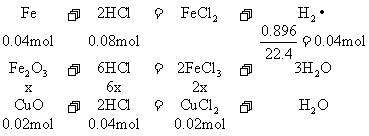
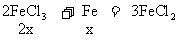
 CuCl2 +
Fe = FeCl2 +Cu
CuCl2 +
Fe = FeCl2 +Cu
1.所谓“守恒”就是以化学反应过程中存在的某些守恒关系如_________守恒、元素守恒、得失__________守恒等作为依据,寻找化学式中__________总数绝对值相等;复分解反应中阴阳离子________________总量相等;氧化还原反应中氧化剂与还原剂_________________________相等。几个连续或平行反应前后某种微粒的_________________相等作为解题的基本思路。运用守恒法解题既可避免书写繁琐的化学方程式,提高解题的速度,又可避免在纷纭复杂的解题背景中寻找关系式,提高解题的准确度。
2.运用化学实验知识,对实验方案作出分析和判断。
[经典题型]实验方案的设计
[例题]
Cu+在酸性溶液中不稳定,可发生自身氧化还原反应生成Cu2+和Cu。现有浓硫酸、浓硝酸、稀硫酸、稀硝酸、FeCl3稀溶液及pH试纸,而没有其它试剂。简述如何用最简便的实验方法来检验CuO经氢气还原所得到的红色产物中是否含有碱性氧化物Cu2O。
[点拔]
CuO经氢气还原所得到的红色产物一定有铜,要检验铜中是否含有Cu2O,应运用Cu2O具有而铜不具有的性质去判断。根据题中所给信息,显然应将Cu2O在酸性溶液中转变为Cu2+,从颜色变化来判断。但Cu也能与氧化性酸反应可转变为Cu2+,故不应使用浓硫酸、浓稀硝酸。
1.根据实验试题要求,设计基本实验方案。
所谓词语的指代义,一般指对文中出现的人称代词和指示代词所替代的对象的理解和确认。代词(包括概括性的词语和运用了修辞的词语)的出现,往往是在所指代的事物、人物之后,因此,代词指代内容的落实在本句是找不到答案的,代词的指代对象一般在上句或上文,我们解题时,一般要从上文中找,而且由近及远地去找,即“取近不取远”。找出所指内容后,要用“代入法”检验,即把指代的具体对象和内容直接代入原句中,看与原文的思路、意思是否一致,以确定答案的正确性。
张炜(09广东卷)
俄国画家列宾给托尔斯泰画了一幅耕作图。它长久地吸引了我,让我想象那个杰出的老人,想象他与土地须叟不可分离的关系。也许这是一个伟大诗人与庸常写作者的最本质、最重要的区别。
在房间里专注于自己的所谓艺术和思想的人,可能不太理解一个耕作的诗人。对于他,稿纸和土地一样,笔和犁一样。于是他的稿纸就相当于一片田园,可以种植,可以催发鲜花、浇灌出果实。在这不息的劳作之中,他寻求着最大的真实,焕发出一个人的全部激情。离开了这些,一切都无从谈起。
在诗人的最重要的几部文学著作之间的长长间隔里,我们都不难发现他怎样匍匐到土地上,与庄园里的农民,特别是孩子和农妇们打成一片,割草、缝鞋子、编识字课本、收割、种植……他做他们所做的一切,身心与土地紧密结合。这对于他,并非完全是刻意如此,而是一个自然而然的过程,他只能如此。他就是这样的一个生命。他在它们中间。①他可以融化在它们之中,融化在泥土之中。
常用的抽样方法及它们之间的联系和区别:
|
类别 |
共同点 |
各自特点 |
相互联系 |
适用范围 |
|
简单随机抽样 |
抽样过程中每个个体被抽取的概率是相同的 |
从总体中逐个抽取 |
|
总体中的个数比较少 |
|
系统抽样 |
将总体均匀分成几个部分,按照事先确定的规则在各部分抽取 |
在起始部分抽样时采用简单随机抽样 |
总体中的个数比较多 |
|
|
分层抽样 |
将总体分成几层,分层进行抽取 |
各层抽样时采用简单抽样或者相同抽样 |
总体由差异明显的几部分组成 |
不放回抽样和放回抽样:在抽样中,如果每次抽出个体后不再将它放回总体,称这样的抽样为不放回抽样;如果每次抽出个体后再将它放回总体,称这样的抽样为放回抽样。
随机抽样、系统抽样、分层抽样都是不放回抽样.
题型1:统计概念及简单随机抽样
例1.为调查参加运动会的1000名运动员的年龄情况,从中抽查了100名运动员的年龄,就这个问题来说,下列说法正确的是( )
A.1000名运动员是总体 B.每个运动员是个体
C.抽取的100名运动员是样本 D.样本容量是100
解析:这个问题我们研究的是运动员的年龄情况,因此应选D。
答案:D
点评:该题属于易错题,一定要区分开总体与总体容量、样本与样本容量等概念。
例2.今用简单随机抽样从含有6个个体的总体中抽取一个容量为2的样本。问:① 总体中的某一个体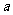 在第一次抽取时被抽到的概率是多少?② 个体
在第一次抽取时被抽到的概率是多少?② 个体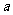 不是在第1次未被抽到,而是在第2次被抽到的概率是多少?③ 在整个抽样过程中,个体
不是在第1次未被抽到,而是在第2次被抽到的概率是多少?③ 在整个抽样过程中,个体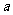 被抽到的概率是多少?
被抽到的概率是多少?
解析:(1)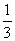 ,(2)
,(2)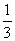 ,(3)
,(3)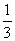 。
。
点评:由问题(1)的解答,出示简单随机抽样的定义,问题( 2
)是本讲难点。基于此,简单随机抽样体现了抽样的客观性与公平性.
题型2:系统抽样
例3.为了了解参加某种知识竞赛的1003名学生的成绩,请用系统抽样抽取一个容量为50的样本。
解析:(1)随机地将这1003个个体编号为1,2,3,…,1003.
(2)利用简单随机抽样,先从总体中剔除3个个体(可利用随机数表),剩下的个体数1000能被样本容量50整除,然后再按系统抽样的方法进行.
点评:总体中的每个个体被剔除的概率相等 ,也就是每个个体不被剔除的概率相等
,也就是每个个体不被剔除的概率相等 .采用系统抽样时每个个体被抽取的概率都是
.采用系统抽样时每个个体被抽取的概率都是 ,所以在整个抽样过程中每个个体被抽取的概率仍然相等,都是
,所以在整个抽样过程中每个个体被抽取的概率仍然相等,都是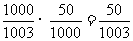 。
。
例4.(2008年湖南理,15)
.对有n(n≥4)个元素的总体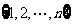 进行抽样,先将总体分成两个子总体
进行抽样,先将总体分成两个子总体
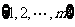 和
和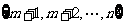 (m是给定的正整数,且2≤m≤n-2),再从
(m是给定的正整数,且2≤m≤n-2),再从
每个子总体中各随机抽取2个元素组成样本.用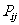 表示元素i和j同时出现在样
表示元素i和j同时出现在样
本中的概率,则 =
; 所有
=
; 所有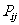 (1≤i<j≤
(1≤i<j≤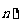 的和等于
.
的和等于
.
[答案] , 6
, 6
[解析]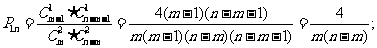 第二空可分:
第二空可分:
①当 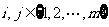 时,
时, 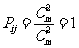 ;
;
②当 
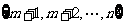 时,
时, 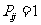 ;
;
③当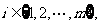
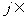
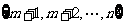 时,
时, 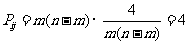 ;
;
 所以
所以

点评:当总体中个体个数较多而差异又不大时可采用系统抽样。采用系统抽样在每小组内抽取时应按规则进行.
(2009年广东卷文)(本小题满分13分)
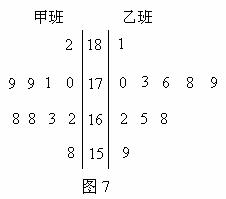
随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图
如图7.
(1)根据茎叶图判断哪个班的平均身高较高;
(2)计算甲班的样本方差
(3)现从乙班这10名同学中随机抽取两名身高不低于173cm的同学,求身高为176cm的同学被抽中的概率.
解析 (1)由茎叶图可知:甲班身高集中于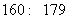 之间,而乙班身高集中于
之间,而乙班身高集中于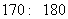 之间。因此乙班平均身高高于甲班;
之间。因此乙班平均身高高于甲班;
(2) 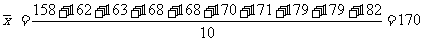
甲班的样本方差为
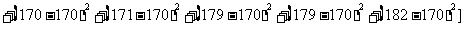 =57
=57
(3)设身高为176cm的同学被抽中的事件为A;
从乙班10名同学中抽中两名身高不低于173cm的同学有:(181,173) (181,176)
(181,178) (181,179) (179,173) (179,176) (179,178) (178,173)
(178, 176) (176,173)共10个基本事件,而事件A含有4个基本事件;
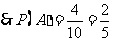 ;
;
题型3:分层抽样
例5.(2009全国卷Ⅱ文)(本小题满分12分)某车间甲组有10名工人,其中有4名女工人;
乙组有10名工人,其中有6名女工人。现采用分层抽样(层内采用不放回简单随即抽样)从甲、乙两组中共抽取4名工人进行技术考核.
(1)求从甲、乙两组各抽取的人数;
(2)求从甲组抽取的工人中恰有1名女工人的概率;
(3)求抽取的4名工人中恰有2名男工人的概率.
解析 本题考查概率统计知识,要求有正确理解分层抽样的方法及利用分类原理处理事件概率的能力,第一问直接利用分层统计原理即可得人数,第二问注意要用组合公式得出概率,第三问关键是理解清楚题意以及恰有2名男工人的具体含义,从而正确分类求概率.
解 (1)由于甲、乙两组各有10名工人,根据分层抽样原理,要从甲、乙两组中共抽
取4名工人进行技术考核,则从每组各抽取2名工人.
(2)记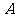 表示事件:从甲组抽取的工人中恰有1名女工人,则
表示事件:从甲组抽取的工人中恰有1名女工人,则
(3)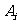 表示事件:从甲组抽取的2名工人中恰有
表示事件:从甲组抽取的2名工人中恰有 名男工人,
名男工人,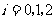
 表示事件:从乙组抽取的2名工人中恰有
表示事件:从乙组抽取的2名工人中恰有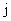 名男工人,
名男工人,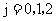
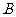 表示事件:抽取的4名工人中恰有2名男工人。
表示事件:抽取的4名工人中恰有2名男工人。
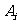 与
与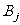 独立,
独立,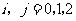 ,且
,且
故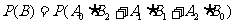
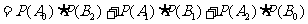
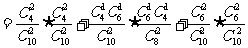
点评:本小题主要考查分层抽样的概念和运算,以及运用统计知识解决实际问题的能力。
例6.甲校有3600名学生,乙校有5400名学生,丙校有1800名学生,为统计三校学生某方面的情况,计划采用分层抽样法,抽取一个样本容量为90人的样本,应在这三校分别抽取学生( )
A.30人,30人,30人 B.30人,45人,15人
C.20人,30人,10人 D.30人,50人,10人
解析:B;
点评:根据样本容量和总体容量确定抽样比,最终得到每层中学生人数。
题型4:综合问题
例7.(1)某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销售点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是
A.分层抽样法,系统抽样法 B.分层抽样法,简单随机抽样法
C.系统抽样法,分层抽样法 D.简单随机抽样法,分层抽样法
分析:此题为抽样方法的选取问题.当总体中个体较多时宜采用系统抽样;当总体中的个体差异较大时,宜采用分层抽样;当总体中个体较少时,宜采用随机抽样.
依据题意,第①项调查应采用分层抽样法、第②项调查应采用简单随机抽样法.故选B.
答案:B
(2)某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,…,270;使用系统抽样时,将学生统一随机编号1,2,…,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况:
①7,34,61,88,115,142,169,196,223,250;
②5,9,100,107,111,121,180,195,200,265;
③11,38,65,92,119,146,173,200,227,254;
④30,57,84,111,138,165,192,219,246,270;
关于上述样本的下列结论中,正确的是 ( )
A.②、③都不能为系统抽样 B.②、④都不能为分层抽样
C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
解析:D。
点评:采用什么样的抽样方法要依据研究的总体中的个体情况来定。
3.分层抽样:当已知总体由差异明显的几部分组成时,常将总体分成几部分,然后按照各部分所占的比进行抽样,这种抽样叫做分层抽样,其中所分成的各部分叫做层.
结论:
(1)分层抽样是等概率抽样,它也是公平的。用分层抽样从个体数为N的总体中抽取一个容量为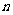 的样本时,在整个抽样过程中每个个体被抽到的概率相等,都等于
的样本时,在整个抽样过程中每个个体被抽到的概率相等,都等于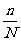 ;
;
(2)分层抽样是建立在简单随机抽样或系统抽样的基础上的,由于它充分利用了已知信息,因此利用它获取的样本更具有代表性,在实践的应用更为广泛.
2.系统抽样:当总体中的个数较多时,可将总体分成均衡的几个部分,然后按照预先定出的规则,从每一部分抽取1个个体,得到所需要的样本,这种抽样叫做系统抽样(也称为机械抽样)。
系统抽样的步骤可概括为:
(1)将总体中的个体编号。采用随机的方式将总体中的个体编号;
(2)将整个的编号进行分段。为将整个的编号进行分段,要确定分段的间隔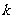 .当
.当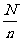 是整数时,
是整数时, ;当
;当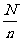 不是整数时,通过从总体中剔除一些个体使剩下的个体数N´能被
不是整数时,通过从总体中剔除一些个体使剩下的个体数N´能被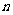 整除,这时
整除,这时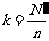 ;
;
(3)确定起始的个体编号。在第1段用简单随机抽样确定起始的个体边号 ;
;
(4)抽取样本。按照先确定的规则(常将 加上间隔
加上间隔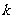 )抽取样本:
)抽取样本: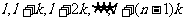 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com