20.已知函数f(x)=ax³-bx²+(2-b)x+1 在x=x₁处取得极大值，在x=x₂处取得极小值，且0<x₁<1<x₂<2.　　　　　 (1)证明a>0;　 　(2)若z=a+2b,求z的取值范围。

19．已知二次函数的二次项系数为a，且不等式的解集为(1，3).

　 (1)若方程有两个相等的根，求的解析式；

　 (2)若的最大值为正数，求a的取值范围.

18.本公司计划2008年在甲、乙两个电视台做总时间不超过300分钟的广告，广告总费用不超过9万元，甲、乙电视台的广告收费标准分别为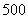元/分钟和200元/分钟，规定甲、乙两个电视台为该公司所做的每分钟广告，能给公司事来的收益分别为0.3万元和0.2万元．问该公司如何分配在甲、乙两个电视台的广告时间，才能使公司的收益最大，最大收益是多少万元？

17.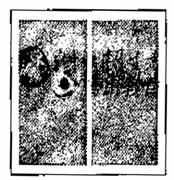如图，要设计一张矩形广告，该广告含有大小相等的左右两个矩形栏目(即图中阴影部分)，这两栏的面积之和为18000cm^2,四周空白的宽度为10cm，两栏之间的中缝空白的宽度为5cm，怎样确定广告的高与宽的尺寸(单位：cm)，能使矩形广告面积最小？

16.某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房。经测算，如果将楼房建为x(x10)层，则每平方米的 平均建筑费用为560+48x(单位：元)。为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？

(注：平均综合费用=平均建筑费用+平均购地费用，平均购地费用=)

15.设函数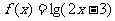的定义域为集合M，函数的定义域为集合N。　　

求： (1)集合M，N；　 (2)集合，。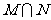

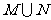14.已知实数x、y满足则z＝2x－y的取值范围是 　___________　 .

13．当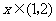时，不等式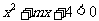恒成立，则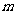的取值范围是　 ______　　 ．

12．已知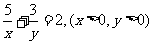,则的最小值是_____________

11．不等式的解集为 　　_________　 　．