
22.(满分14分)
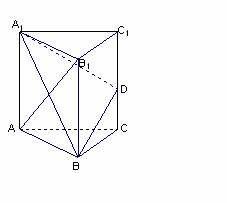 如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为
如图,已知三棱柱ABC-A1B1C1的所有棱长都相等,且侧棱垂直于底面,由B沿棱柱侧面经过棱C C1到点A1的最短路线长为 ,设这条最短路线与CC1的交点为D. K^S*5U.C#
,设这条最短路线与CC1的交点为D. K^S*5U.C#
(Ⅰ)求三棱柱ABC-A1B1C1的体积;
(Ⅱ)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(Ⅲ)证明:平面A1BD⊥平面A1ABB1
21.(满分12分)
在棱长为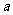 的正方体
的正方体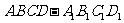 中,
中,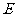 、
、 分别是
分别是 、
、 的中点,
的中点, 与
与 交于点
交于点 ,
, 为棱上
为棱上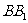 一点.
一点.
 (Ⅰ)
(Ⅰ)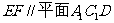 ;
;
(Ⅱ)当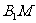 :
: 的值为多少时,
的值为多少时, ⊥平面
⊥平面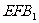 ,证明之;
,证明之;
(Ⅲ)求点 到平面
到平面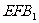 的距离.
的距离.
20.(满分12分)
如图(1),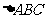 是等腰直角三角形,
是等腰直角三角形,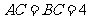 ,
,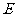 、
、 分别为
分别为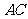 、
、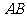 的中点,将
的中点,将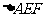 沿
沿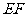 折起,使
折起,使 在平面
在平面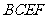 上的射影
上的射影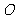 恰为
恰为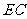 的中点,得到图(2).
的中点,得到图(2).
 (Ⅰ)求证:
(Ⅰ)求证: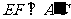 ;
;
 (Ⅱ)求三棱锥
(Ⅱ)求三棱锥 的体积.
的体积.
图(1) 图(2)
19. (满分12分)
(满分12分)
如图组合体中,三棱柱 的侧面
的侧面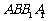 是圆柱的轴截面,
是圆柱的轴截面,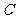 是圆柱底面圆周上不与
是圆柱底面圆周上不与 、
、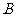 重合一个点.
重合一个点.
(Ⅰ)求证:无论点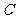 如何运动,平面
如何运动,平面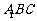
 平面
平面 ;
;
(Ⅱ)当点 是弧
是弧 的中点时,求四棱锥
的中点时,求四棱锥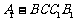 与圆柱的体积比.
与圆柱的体积比.
18.(满分12分)
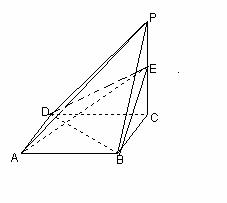
已知一四棱锥P-ABCD的三视图如下,E是侧棱PC上的动点。
(Ⅰ)是否不论点E在何位置,都有BD⊥AE?证明你的结论;
(Ⅱ)若点E为PC的中点,求证 ;
;
(III)求由点A绕四棱锥P-ABCD的侧面一周回到点A的最短距离
17. (满分12分)
(满分12分)
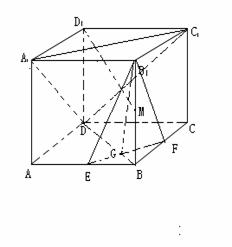
如图,在长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,
G是CC1上的动点。
(Ⅰ)求证:平面ADG⊥平面CDD1C1
(Ⅱ)判断B1C1与平面ADG的位置关系,并给出证明;
 (III)求三棱锥D1-ADG的体积.
(III)求三棱锥D1-ADG的体积.
16. 已知一几何体的三视图如下,正视图和侧视图都是矩形,俯视图为正方形,
已知一几何体的三视图如下,正视图和侧视图都是矩形,俯视图为正方形,
在该几何体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,
这些几何形体是 (写出所有正确结论的编号).
①矩形;
②不是矩形的平行四边形;
③有三个面为直角三角形,有一个面为等腰三角形的四面体;
④每个面都是等腰三角形的四面体; K^S*5
⑤每个面都是直角三角形的四面体
15. 在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则
在Rt△ABC中,CA⊥CB,斜边AB上的高为h1,则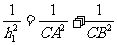 ;类比此性质,
;类比此性质,
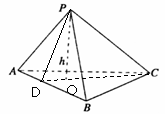
如图,在四面体P-ABC中,若PA,PB,PC两两垂直,底面ABC上的高为h,
则得到的正确结论为 ; K^S*5
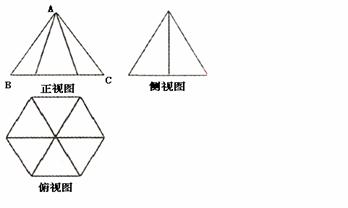
14.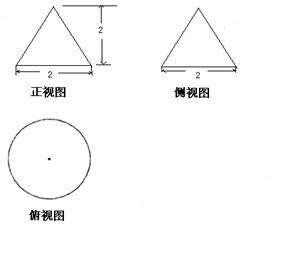 一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为
.
一个几何的三视图如图所示:其中,正视图中△ABC的边长是2的正三角形,俯视图为正六边形,那么该几何体几的体积为
.
 |
|||||
|
|
||||
13.一个几何体的三视图如图所示,则该几何体外接球的表面积为____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com