
10.今有2个红球、3个黄球、4个白球,同色球不加以区分,将这9个球排成一列有 ___ __ 种不同的方法(用数字作答)。
 11. 从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有 个。(用数字作答)
11. 从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数字的四位数,其中能被5整除的四位数共有 个。(用数字作答)
9.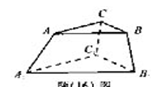 某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如题图所示的6个点A、B、C、A1、B1、C1上各安装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有 种(用数字作答).
某人有3种颜色的灯泡(每种颜色的灯泡足够多),要在如题图所示的6个点A、B、C、A1、B1、C1上各安装一个灯泡,要求同一条线段两端的灯泡不同色,则不同的安装方法共有 种(用数字作答).
7.从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任), 要求这3位班主任中男、女教师都要有,则不同的选派方案共有____________________.
8从黄瓜、白菜、油菜、扁豆4种蔬菜品种中选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共有__________________.
6.某通讯公司推出一组手机卡号码,卡号的前七位数字固定,从“×××××××0000”到“×××××××9999”共10000个号码.公司规定:凡卡号的后四位带有数字“4”或“7”的一律作为“优惠卡”,则这组号码中“优惠卡”的个数为___________________.
5.将标号为1,2,…,10的10个球放入标号为1,2,…,10的10个盒子里,
每个盒内放一个球,恰好3个球的标号与其在盒子的标号不一致的放入方法
种数为_________________.
4.将1,2,3填入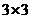 的方格中,要求每行、每列都没有重复数字,
的方格中,要求每行、每列都没有重复数字,
右面是一种填法,则不同的填写方法共有____________.
2.设直线的方程是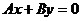 ,从1,2,3,4,5这五个数中每次取两个不同的数作为A、 B的值,则所得不同直线的条数是__________________.
,从1,2,3,4,5这五个数中每次取两个不同的数作为A、 B的值,则所得不同直线的条数是__________________.
 3.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有_________________.
3.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有_________________.
1.某班级要从4名男生和2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方法有__________________.
20.(Ⅰ)解法一:由题意知,ε的可能取值为0,1,2,3,且
所以ε的分布列为
|
ε |
0 |
1 |
2 |
3 |
|
P |
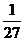 |
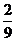 |
 |
 |
ε的数学期望为Eε=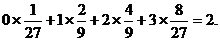
解法二:根据题设可知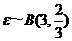
因此ε的分布列为
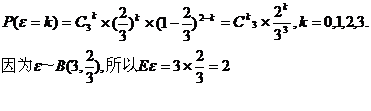
(Ⅱ)解法一:用C表示“甲得2分乙得1分”这一事件,用D表示“甲得3分乙得0分”这一事件,所以AB=C∪D,且C、D互斥,又
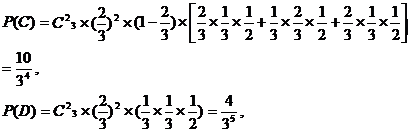
由互斥事件的概率公式得
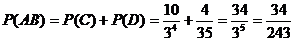
 解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
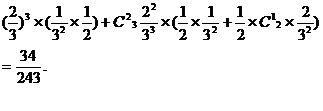
19.(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件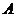 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件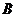 .由于事件
.由于事件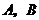 相互独立,且
相互独立,且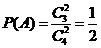 ,
, .
.
故取出的4个球均为黑球的概率为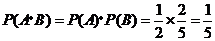 .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件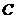 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件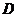 .由于事件
.由于事件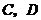 互斥,
互斥,
且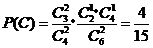 ,
, .
.
故取出的4个球中恰有1个红球的概率为 .
.
(Ⅲ)解: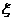 可能的取值为
可能的取值为 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得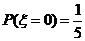 ,
, ,
,
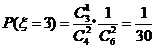 .从而
.从而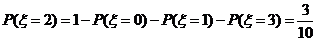 .
.
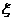 的分布列为
的分布列为
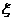 |
0 |
1 |
2 |
3 |
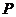 |
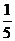 |
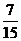 |
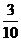 |
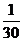 |
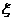 的数学期望
的数学期望 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com