
1.原点到直线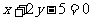 的距离为________________.
的距离为________________.
20.解:(Ⅰ)
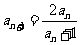 ,
,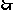
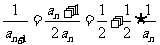 ,
,
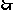
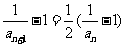 ,又
,又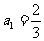 ,
,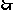
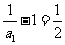 ,
,
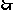 数列
数列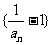 是以为
是以为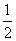 首项,
首项,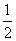 为公比的等比数列.
为公比的等比数列.
(Ⅱ)由(Ⅰ)知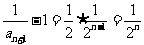 ,即
,即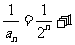 ,
,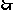
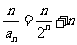 .
.
设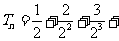 …
…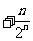 , ①
, ①
则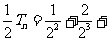 …
…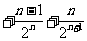 ,②
,②
由①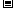 ②得
②得
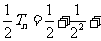 …
… ,
,
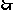
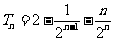 .又
.又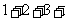 …
…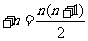 .
.
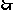 数列
数列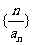 的前
的前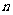 项和
项和
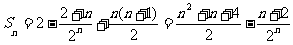
19.(Ⅰ)解:设等比数列 以比为
以比为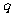 ,则
,则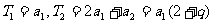 。………2分
。………2分
∵ ,
,
∴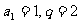 。
…………5分
。
…………5分
(Ⅱ)解法一:由(Ⅰ)知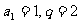 ,故
,故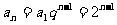 ,
,
因此,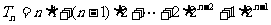 ,
…………8分
,
…………8分
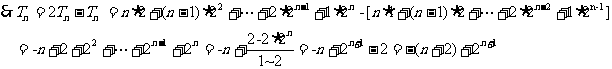 解法二:设
解法二:设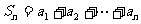 。 由(Ⅰ)知
。 由(Ⅰ)知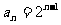 。
。
∴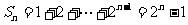 …………8分
…………8分
∴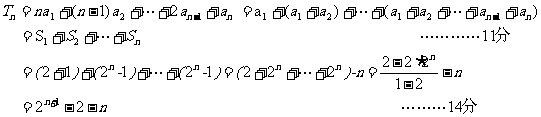
18.解:∵ {an}为等差数列,{bn}为等比数列,∴ a2+a4=2a3,b3b4=b32,
而已知a2+a4=b3,b3b4=a3, ∴ b3=2a3,a3=b32. ∵ b3≠0,∴ b3=,a3= 由 a1=1,a3= 知{an}的公差d=- ∴ S10=10a1+ 由b1=1,b3= 知{bn}的公比为q=或q=- 当q=时,T10= 当q=-时,T10=
17.解:(I)设等比数列{an}的公比为q,则a2=a1q,
a5=a1q4. 依题意,得方程组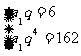
解此方程组,得a1=2, q=3. 故数列{an}的通项公式为an=2·3n-1.
(II) 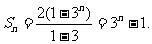
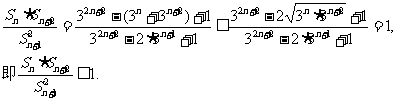
16.解:由题设知 ,
,
则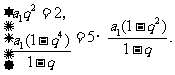 ②
②
由②得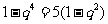 ,
,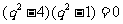 ,
, ,
,
因为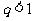 ,解得
,解得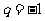 或
或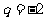 .
.
当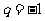 时,代入①得
时,代入①得 ,通项公式
,通项公式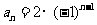 ;
;
当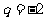 时,代入①得
时,代入①得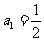 ,通项公式
,通项公式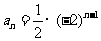 .
.
15.解: 设等比数列{an}的公比为q, 则q≠0, a2= = , a4=a3q=2q
所以 + 2q= , 解得q1= , q2= 3,
当q=时, a1=18.所以 an=18×()n-1= = 2×33-n.
当q=3时, a1= , 所以an=×3n-1=2×3n-3.
11.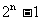 ; 12.
; 12.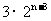 ; 13.
; 13.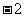 ; 14.4
; 14.4
1. 127 2. 16 3. 2
4. 84 5. 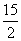 6. 120 7.
6. 120 7. 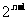 8.
8. 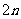 9. -4 10. 2
9. -4 10. 2
14.等比数列试题(自我测试)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com