
4.将1,2,3填入 的方格中,要求每行、每列都没有重复数字,
的方格中,要求每行、每列都没有重复数字,
右面是一种填法,则不同的填写方法共有____________.
2.设直线的方程是 ,从1,2,3,4,5这五个数中每次取两个不同的数作为A、 B的值,则所得不同直线的条数是__________________.
,从1,2,3,4,5这五个数中每次取两个不同的数作为A、 B的值,则所得不同直线的条数是__________________.
 3.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有_________________.
3.某外商计划在四个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有_________________.
1.某班级要从4名男生和2名女生中选派4人参加某次社区服务,如果要求至少有1名女生,那么不同的选派方法有__________________.
20.(Ⅰ)解法一:由题意知,ε的可能取值为0,1,2,3,且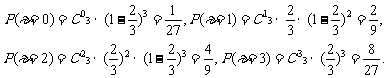
所以ε的分布列为
|
ε |
0 |
1 |
2 |
3 |
|
P |
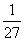 |
 |
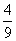 |
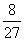 |
ε的数学期望为Eε=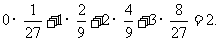
解法二:根据题设可知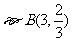
因此ε的分布列为
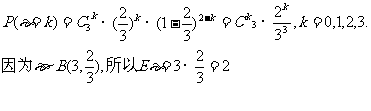
(Ⅱ)解法一:用C表示“甲得2分乙得1分”这一事件,用D表示“甲得3分乙得0分”这一事件,所以AB=C∪D,且C、D互斥,又

由互斥事件的概率公式得
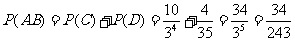
 解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
解法二:用Ak表示“甲队得k分”这一事件,用Bk表示“已队得k分”这一事件,k=0,1,2,3由于事件A3B0,A2B1为互斥事件,故P(AB)=P(A3B0∪A2B1)=P(A3B0)+P(A2B1).
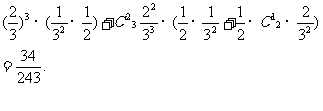
19.(Ⅰ)解:设“从甲盒内取出的2个球均为黑球”为事件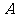 ,“从乙盒内取出的2个球均为黑球”为事件
,“从乙盒内取出的2个球均为黑球”为事件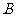 .由于事件
.由于事件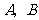 相互独立,且
相互独立,且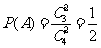 ,
,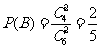 .
.
故取出的4个球均为黑球的概率为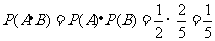 .
.
(Ⅱ)解:设“从甲盒内取出的2个球均为黑球;从乙盒内取出的2个球中,1个是红球,1个是黑球”为事件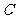 ,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件
,“从甲盒内取出的2个球中,1个是红球,1个是黑球;从乙盒内取出的2个球均为黑球”为事件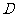 .由于事件
.由于事件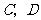 互斥,
互斥,
且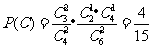 ,
,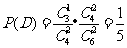 .
.
故取出的4个球中恰有1个红球的概率为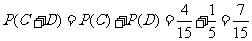 .
.
(Ⅲ)解: 可能的取值为
可能的取值为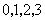 .由(Ⅰ),(Ⅱ)得
.由(Ⅰ),(Ⅱ)得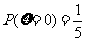 ,
,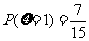 ,
,
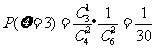 .从而
.从而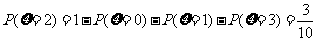 .
.
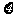 的分布列为
的分布列为
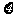 |
0 |
1 |
2 |
3 |
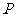 |
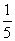 |
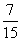 |
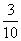 |
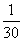 |
 的数学期望
的数学期望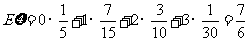 .
.
18.[答案]:(I)基本事件总数为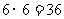 ,
,
若使方程有实根,则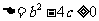 ,即
,即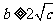 。
。
当 时,
时,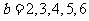 ; 当
; 当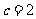 时,
时,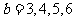 ; 当
; 当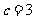 时,
时,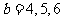 ;
;
当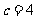 时,
时,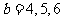 ;
当
;
当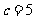 时,
时,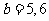 ;
当
;
当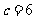 时,
时,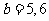 ,
,
目标事件个数为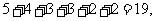
因此方程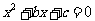 有实根的概率为
有实根的概率为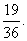
(II)由题意知,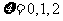 ,则
,则  ,
,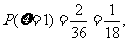
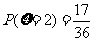 ,
,
故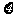 的分布列为
的分布列为
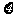 |
0 |
1 |
2 |
|
P |
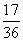 |
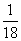 |
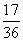 |
 的数学期望
的数学期望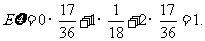
(III)记“先后两次出现的点数中有5”为事件M,“方程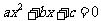 有实根” 为事件N,
有实根” 为事件N,
则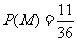 ,
, 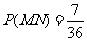 ,
,  .
.
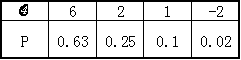
17.解: (1) 依题意得, ξ的所有可能取值为6,2,1,-2.
ξ=6,2,1,-2分别对应抽取1件产品为一等品、二等品、三等品、次品这四个事件.
所以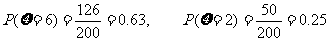 ,
,
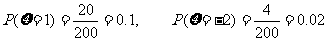 ,
,
所以ξ的分布列为
(2) 1件产品的平均利润为Eξ=6 0.63+2
0.63+2 0.25+1
0.25+1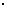 0.1-2
0.1-2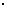 0.02=4.34
0.02=4.34
(3)设三等品率为x,则二等品率为0.29-x,此时ξ的分布列为

1件产品的平均利润为Eξ=6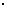 0.7+2
0.7+2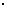 (0.29-x)+x-2
(0.29-x)+x-2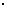 0.01=4.76-x
0.01=4.76-x
令Eξ=4.76-x 4.73,解得
4.73,解得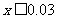 =3%,
=3%,
答:三等品率最多是3%.
16.[解]:记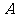 表示事件:进入商场的1位顾客购买甲种商品,
表示事件:进入商场的1位顾客购买甲种商品,
记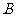 表示事件:进入商场的1位顾客购买乙种商品,
表示事件:进入商场的1位顾客购买乙种商品,
记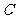 表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
记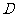 表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
表示事件:进入商场的1位顾客至少购买甲、乙两种商品中的一种,
(Ⅰ)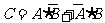
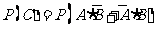
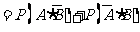
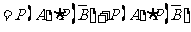
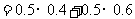
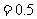
(Ⅱ)
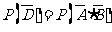

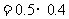
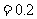 ,
, 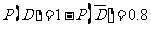
(Ⅲ)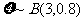 ,故
,故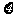 的分布列
的分布列
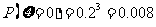 ,
,
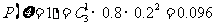
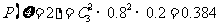 ,
, 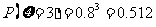
所以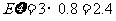
15.解: (Ⅰ)记"甲投篮1次投进"为事件A1 , "乙投篮1次投进"为事件A2 , "丙投篮1次投进"为事件A3, "3人都没有投进"为事件A . 则 P(A1)= , P(A2)= , P(A3)= ,
∴ P(A) = P()=P()·P()·P()
= [1-P(A1)] ·[1-P (A2)] ·[1-P (A3)]=(1-)(1-)(1-)=
∴3人都没有投进的概率为 .
(Ⅱ)解法一: 随机变量ξ的可能值有0,1,2,3), ξ~ B(3, ),
P(ξ=k)=C3k()k()3-k (k=0,1,2,3) , Eξ=np = 3× = .
解法二: ξ的概率分布为:
|
ξ |
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
Eξ=0×+1×+2×+3×= 。
11. 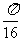 12. 0.3 , 13. 0.8
14. 0.94
12. 0.3 , 13. 0.8
14. 0.94
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com