
1关于做匀速圆周运动的物体,下列说法正确的是( )
A.线速度不变 B.角速度不变 C.向心加速度不变 D.向心力不变
2下列说法中正确的是( )
A.若物体做曲线运动,则其加速度可能是不变的
B.若物体做曲线运动,则其加速度一定是变化的
C.物体在恒力作用下,不可能做曲线运动
D.物体在变力的作用下,不可能做直线运动
3一物体静止在升降机的水平底板上,在升降机加速上升的过程中,下列说法正确的是( )
A.重力对物体做正功 
B.底板对物体的支持力做正功
C.底板对物体的支持力不做功
D.合外力对物体不做功
4一物体做自由落体运动,在第1s末和第2s末重力做功的瞬时功率之比分别为( )
A.1:2 B. 1:3 C. 1:4 D. 1:9
5一艘船以相对于静水恒定的速率渡河,水流速度也恒定(且小于船速),若河的宽度一定,要使船到达对岸航程最短,则( )
A.船头指向应垂直河岸航行 B.船头指向应偏向下游一侧
C.船头指向应偏向上游一侧 D.船不可能沿直线到达对岸
6物体以5m/s的初速度做竖直上抛运动,g取10m/s2,物体能上升的最大高度是( ):A.0.5m B.1.25m C.2.5m D.5m
7某卫星绕地球做匀速圆周运动,若其轨道半径越小,则( ) A.线速度越小,周期越大 B.线速度越大,周期越小 C.角速度越小,周期越大 D.加速度越大,周期越大
8以10m/s的速度水平抛出一物体,不计空气阻力,取g = 10m/s2,当物体的竖直位移大小为0.8m时,其水平位移大小为( )
A.1.6m B.2m C.4m D.40m
9如图所示的皮带传动装置中,皮带与轮之间不打滑,两轮半径分别为R和r,且R=3r,A、B分别为两轮边缘上的点,则皮带轮运动过程中,关于A、B两点下列说法正确的是( )
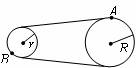 A.角速度之比ωA︰ωB =3︰1:
A.角速度之比ωA︰ωB =3︰1:
B.向心加速度之比aA︰aB =1︰3
C.速率之比υA︰υB =1︰3
D.在相同的时间内通过的路程之比sA︰sB =3︰1
10设地球表面重力加速度为g0,物体在距离地面高度为3R(R是地球的半径)处,由于地球的作用而产生的加速度为g,则为( )
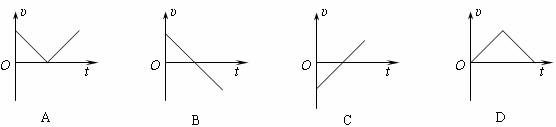
11物体竖直上抛后又落向地面,不计空气阻力,则它在整个过程中速度大小υ跟时间t的关系是可能是图中的( )
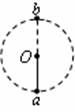 12如图,细杆的一端与一小球相连,可绕过O点的水平轴自由转动,现给小球一初速度,使它在竖直平面内做圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则杆对球的作用力情况是( )
A.a处可能是压力
B.b处一定是拉力
C.b处一定是支持力 D.b处可能没有弹力
12如图,细杆的一端与一小球相连,可绕过O点的水平轴自由转动,现给小球一初速度,使它在竖直平面内做圆周运动,图中a、b分别表示小球轨道的最低点和最高点,则杆对球的作用力情况是( )
A.a处可能是压力
B.b处一定是拉力
C.b处一定是支持力 D.b处可能没有弹力
22、(本小题14分)
已知过点A(0, 1)且斜率为k的直线l,圆C的方程: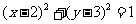 ,
O为坐标原点。
,
O为坐标原点。
(1)若点P在圆C上移动,求线段AP的中点Q的轨迹方程。
(2)是否存在直线l与圆C交于M、N两点,直线OM的斜率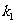 ,直线ON的斜率
,直线ON的斜率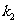 ,满足 ,若存在,求直线l的方程,若不存在,说明理由?
,满足 ,若存在,求直线l的方程,若不存在,说明理由?
21、(本小题12分)
某渔业公司年初用72万元购买一艘捕鱼船,第一年各种费用12万元,以后每年的费用比上一年增加4万元,每年捕鱼收益50万元。
(1)问第几年公司开始获利?
(2)假设若干年后,该公司有两种方案处理这艘捕鱼船:
第一方案:年平均获利最大时,以26万元出售渔船;
第二方案:总获利最大时,以8万元出售渔船;
如果你是该公司老板,你该选择哪种方案?说明理由。
20、(本小题12分)
已知直线l过点P(1, 2),直线l与x、y轴的正半轴分别交于A、B两个不同点,O为坐标原点, 且△OAB面积为4.:
(1)求直线l方程;
(2)求△OAB的外接圆方程。
19、(本小题12分)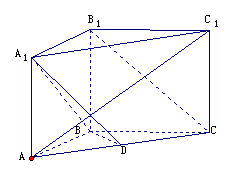
在直三棱柱ABC-A1B1C1(直棱柱指侧棱垂直于底面),AB=BB1=BC,∠ABC是直角,D为AC的中点。
(1)说明AC1与平面ABB1A1所成角θ,求角θ的正切值;
(2)求证:A1B⊥平面AB1C1;
(3)求证:B1C//平面A1BD。
18、(本小题12分)
已知等差数列满足: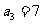 ,
,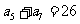 ,设
,设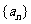 的前n项和为
的前n项和为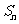 。
。
(1)求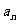 及
及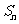 ;
;
(2)令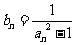 (
(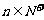 ),求数列
),求数列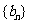 的前n项和
的前n项和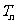 。
。
17、(本小题12分)
在△ABC中,角A、B、C对边分别是a,b,c.若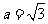 ,
,
(1)求角A
(2)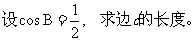
16、设 、
、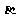 表示平面,
表示平面,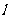 、
、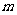 、
、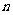 表示不在
表示不在 内也不在
内也不在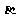 内的直线,给出下列命题:
内的直线,给出下列命题:
① 若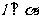 ,
,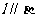 ,则
,则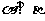 ②若
②若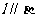 ,
,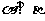 ,则
,则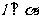
③ 若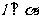 ,
,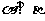 ,则
,则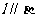 ④若
④若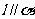 ,
,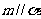 ,则
,则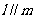
⑤若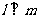 ,
,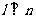 ,则
,则 其中正确的命题是___________
其中正确的命题是___________
15、设x,y满足约束条件 ,则z=x+2y的最小值是
,则z=x+2y的最小值是
14、在空间坐标系中,已知A(1, -2, 1),B(2, 2, 2),点P在z轴上,且|PA|=|PB|,则点P的坐标为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com