2．2009年10月29日-30日，全国未成年人思想道德建设交流会在长沙举行。李长春在讲话中强调，加强和改进未成年人思想道德建设，是关系中华民族伟大复兴的战略工程，是关系中国特色社会主义事业兴旺发达的希望工程，是关系千家万户切身利益的民心工程，是社会主义精神文明建设的基础工程。这段讲话的根据在于(　)

①培育“四有公民”是社会主义精神文明建设的根本任务

②优秀文化为人的健康成长提供不可缺少的精神食粮，对促进人的全面发展起着不可替代的作用

③青少年是国家的希望，民族的未来，社会主义现代化建设有赖于青少年素质的提高

④加强青少年思想道德建设有助于他们树立科学的世界观和人生观

A．①②③ 　　　　　　　　　B．②③④

C．①②④ 　　　　　　　　　D．①②③④

解析：选D。本题考查加强青少年思想道德建设的文化生活道理。四个组合选项均符合题意。

1．社会主义市场经济的发展，催生了许多富有时代气息的思想道德观念。与此同时，落后文化、腐朽文化也利用市场经济的弱点，侵袭人们的思想、败坏人们的道德观念。这说明(　)

A．社会主义思想道德体系与社会主义市场经济是对立的

B．搞市场经济必然导致人们思想道德水平的下降

C．社会主义市场经济越发展，越需要不断丰富社会主义思想道

德的内容

D．要提高人们的思想道德水平，就不能发展社会主义市场经济

解析：选C。A、B、D割裂了社会主义思想道德与社会主义市场经济的关系，说法错误。正确认识社会主义思想道德与社会主义市场经济的关系是做好本题的关键，在二者的关系上，最易犯的错误就是把二者对立起来。而事实上，二者在本质上是内在统一的：一方面，社会主义思想道德能够保证社会主义市场经济的健康发展；另一方面，社会主义市场经济的发展也丰富着社会主义思想道德的内容。答案应为C。

21.已知数列{a_n}中，a₁>0, 且a_n+1=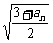，　 (Ⅰ)试求a₁的值，使得数列{a_n}是一个常数数列；

(Ⅱ)试求a₁的取值范围,使得a_n+1>a_n对任何自然数n都成立；

(Ⅲ)若a₁ = 2，设b_n = | a_n+1－a_n| (n = 1，2，3，…)，并以S_n表示数列{b_n}的前n项的和，求证：S_n<．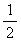

[思路分析]：解：(Ⅰ)欲使数列{a_n}是一个常数数列，则a_n+1=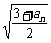= a_n ……………………2’

又依a₁>0，可得a_n>0并解出：a_n=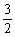，即a₁ = a_n = 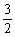……………………4’

(Ⅱ)研究a_n+1－a_n=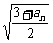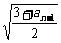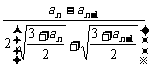－= (n≥2) 　注意到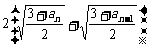>0

因此，可以得出：a_n+1－a_n，a_n－a_n－1，a_n－1－a_n－2，…，a₂－a₁有相同的符号……………7’

要使a_n+1>a_n对任意自然数都成立,只须a₂－a₁>0即可.由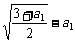>0，解得：0<a₁<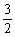………………9’

(Ⅲ)用与(Ⅱ)中相同的方法，可得　 当a₁>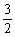时，a_n+1<a_n对任何自然数n都成立.

因此当a₁=2时，a_n+1－a_n<0　　　 ……………………………………………10’

∴　 S_n= b₁+b₂+…b_n=|a₂－a₁| + |a₃－a₂| +…+ |a_n+1－a_n|=a₁－a₂+a₂－a₃+…+a_n－a_n+1

=a₁－a_n+1=2－a_n+1 ………………………………………………………13’

又：a_n+2=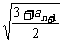< a_n+1，可解得a_n+1>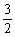, 故S_n<2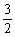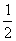－=………………………………………14’

20．已知函数f(x)＝－x³+ax在(0，1)上是增函数．(1)　求实数a的取值集合A；

(2)　当a取A中最小值时，定义数列{a_n}满足：2a_n+1＝f(a_n)，且a₁＝b∈(0，1)(b为常数)，试比较a_n+1与a_n的大小；　 (3)　在(2)的条件下，问是否存在正实数c．使0<＜2对一切n∈N^＊恒成立？

(1)f'(x)＝3x²+a＞0，对x∈(0，1)恒成立，求出a≥3．………………4分

(2)当a＝3时，由题意：a_n+1＝－a+a_n，且a₁＝b∈(0，1)

　以下用数学归纳法证明：a_n∈(0，1)，对n∈N^＊恒成立．

①当n＝1时，a₁＝b∈(0，1)成立；………………………………………………6分

②假设n＝k时，a_k∈(0，1)成立，那么当n＝k+1时，　　 a_k+1＝a_k³+a_k，由①知g(x)＝(－x³+3x)

在(0，1)上单调递增，∴g(0)＜g(a_k)＜g(1)　　 即0＜a_k+1＜1，　由①②知对一切n∈N^＊都有a_n∈(0，1)　　 　

而a_n+1－a_n＝－a_n³+a_n－a_n＝a_n(1－a_n²)＞0　 ∴a_n+1＞a_n…………………………………10分

(3)存在正实数c，使0＜＜2恒成立,令y＝＝1+，在(c，+∞)上是减数，

∴随着a_n增大，而小，　 　又{a_n}为递增数列，所以要使0＜＜2恒成立，

只须∴0＜c＜，即0＜c＜　　　　　 ………　　 14分

19．已知f(x+1)=x²－4,等差数列{a_n}中,a₁=f(x－1), a₂=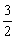－,a₃=f(x)．(1)求x值；(2)求a₂+a₅+a₈+…+a₂₆的值．

[解] (1)∵f(x－1)=(x－1－1)²－4=(x－2)²－4　　 ∴f(x)=(x－1)²－4,∴a₁=(x－2)²－4,a₃=(x－1)²－4

又a₁+a₃=2a₂,解得x=0或x=3．

(2)∵a₁、a₂、a₃分别为0、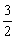－、－3或－3、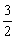－、0　　　 ∴a_n=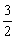－(n－1)或a_n=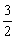(n－3)

①当a_n=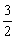－(n－1)时，a₂+a₅+…+a₂₆=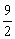(a₂+a₂₆)=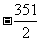

②当a_n=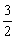(n－3)时，a₂+a₅+…+a₂₆=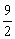(a₂+a₂₆)=．

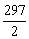18．设等差数列{a_n}共有3n项，它的前2n项和为100，后2n项和是200，则该数列的中间n项和等于　 75　 ．

17．一个等差数列的前12项的和为354，前12项中，偶数项和与奇数项和之比为32∶27，则公差d等于__5　 _．

16．等差数列{a_n}中，若a₃+a₅=a₇－a₃=24,则a₂=___0___．

15．已知等差数列{a_n}的公差d =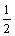，且前100项和S­₁₀₀ = 145，那么a₁ + a₃ + a₅ +…+a₉₉ =　 60　 .

14．等差数列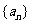中,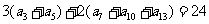,则此数列前13项和是_____26_____．