2．太阳系中类地行星的特点是　　 (　　 )

　 A.质量较大 　　B.卫星较多 　　C.平均密度较大　　 D.体积较大

1．类地行星与巨行星相比　　 ( 　　)

　 A.质量较大　　 B.距太阳近　 　　C.体积大　 　　　　D.表面温度较低

22.(本小题满分12分)

设椭圆C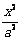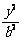：+＝1(a＞b＞0)的左焦点为F，过点F的直线与椭圆C相交于A，B两点，直线l的倾斜角为60°，AF＝2FB.

(I)求椭圆C的离心率；

(II)如果|AB|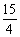＝，求椭圆C的方程.

玉溪一中高2011届高二下学期期末考试数学试题(理科)

21.(本小题满分12分)

已知函数f(x)＝x²(x－3a)+1 (a＞0，x∈R).

(I)求函数y＝f(x)的极值；

(II)函数y＝f(x)在(0，2)上单调递减，求实数a的取值范围；

(III)若在区间(0，+∞)上存在实数x₀，使得不等式f(x₀)－4a³≤0能成立，求实数a的取值范围.

20.(本小题满分12分)

某同学参加3门课程的考试.假设该同学第一门课程取得优秀成绩的概率为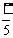，第二、第三门课程取得优秀成绩的概率分别为p，q(p＞q)，且不同课程是否取得优秀成绩相互独立，记ξ为该生取得优秀成绩的课程数，其分布列为

ξ	0	1	2	3
p		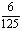a	b

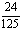(I)求该生至少有1门课程取得优秀成绩的概率；

(II)求p，q的值；

(III)求数学期望Eξ.

19.(本小题满分12分)

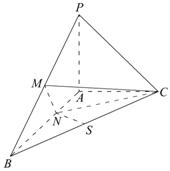
如图，已知三棱锥P-ABC中，PA⊥平面ABC，

AB⊥AC，PA＝AC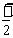＝AB，N为AB上一点，

AB＝4AN，M，S分别为PB，BC的中点.

(I)证明：CM⊥SN；

(II)求SN与平面CMN所成角的大小.

18.(本小题满分12分)

已知m＝(cosωx+sinωx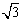，cosωx)，n＝(cosωx－sinωx，2sinωx)，其中ω＞0，若函数f(x)＝m·n，且f(x)的对称中心到f(x)的对称轴的最近距离不小于.

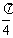(I)求ω的取值范围；

(II)在△ABC中，a，b，c分别是内角A，B，C的对边，且a＝1，b+c＝2，当ω取最大值时，f(A)＝1，求△ABC的面积.

17.(本小题满分10分)

已知等比数列{a_n}中，S_n为其前n项和，且a₁+a₃＝5，S₄＝15，设b_n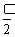＝+，求数列{b_n}的前n项和T_n .

16.函数f(x)＝x³+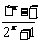+3sinx+4在区间[－t，t](t＞0)上的最大值与最小值之和为　　　　 .

15.设抛物线y²＝2Px(P＞0)的焦点为F，点A(0，2).若线段FA的中点B在抛物线上，则B到该抛物线准线的距离为　　　　 .