26．(本小题满分12分)

某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．

若只在国内销售，销售价格y(元/件)与月销量x(件)的函数关系式为y =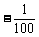x+150，

成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w_内(元)(利润　=　销售额－成本－广告费)．

若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件(a为

常数，10≤a≤40)，当月销量为x(件)时，每月还需缴纳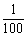x²　元的附加费，设月利润为w_外(元)(利润　=　销售额－成本－附加费)．

(1)当x　=　1000时，y　=　　　　 元/件，w_内=　　　　 元；

(2)分别求出w_内，w_外与x间的函数关系式(不必写x的取值范围)；

(3)当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；

(4)如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？

参考公式：抛物线的顶点坐标是．

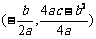汪国刚 贵州省贵阳市开阳县宅吉中学550308

2010年河北省初中毕业生升学文化课考试

25．(本小题满分12分)

如图16，在直角梯形ABCD中，AD∥BC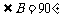，，AD　=　6，BC　=　8，，点M是BC的中点．点P从点M出发沿MB以每秒1个单位长的速度向点B匀速运动，到达点B后立刻以原速度沿BM返回；点Q从点M出发以每秒1个单位长的速度在射线MC上匀速运动．在点P，Q的运动过程中，以PQ为边作等边三角形EPQ，使它与梯形ABCD在射线BC的同侧．点P，Q同时出发，当点P返回到点M时停止运动，点Q也随之停止．

设点P，Q运动的时间是t秒(t＞0)．

(1)设PQ的长为y，在点P从点M向点B运动的过程中，写出y与t之间的函数关系式(不必写t的取值范围)．

(2)当BP　=　1时，求△EPQ与梯形ABCD重叠部分的面积．

(3)随着时间t的变化，线段AD会有一部分被△EPQ覆盖，被覆盖线段的长度在某个时刻会达到最大值，请回答：该最大值能否持续一个时段？若能，直接写出t的取值范围；若不能，请说明理由．

24．(本小题满分10分)

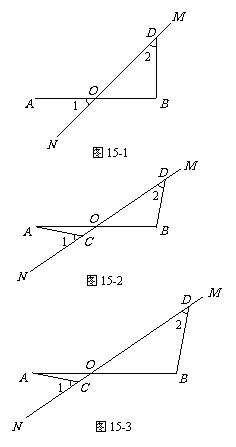
在图15-1至图15-3中，直线MN与线段AB相交

于点O，∠1　=　∠2　=　45°．

(1)如图15-1，若AO　=　OB，请写出AO与BD

的数量关系和位置关系；

(2)将图15-1中的MN绕点O顺时针旋转得到

图15-2，其中AO　=　OB．

求证：AC　=　BD，AC　⊥　BD；

(3)将图15-2中的OB拉长为AO的k倍得到

图15-3，求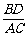的值．

23．(本小题满分10分)

观察思考

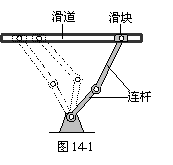
某种在同一平面进行传动的机械装置如图14-1，图14-2

是它的示意图．其工作原理是：滑块Q在平直滑道l上可以

左右滑动，在Q滑动的过程中，连杆PQ也随之运动，并且

PQ带动连杆OP绕固定点O摆动．在摆动过程中，两连杆的接点P在以OP为半径的⊙O上运动．数学兴趣小组为进一步研

究其中所蕴含的数学知识，过点O作OH　⊥l于点H，并测得

OH　=　4分米，PQ　=　3分米，OP　=　2分米．

解决问题

(1)点Q与点O间的最小距离是　　　　 分米；

点Q与点O间的最大距离是　　　　 分米；

点Q在l上滑到最左端的位置与滑到最右端位置间

的距离是　　　　 分米．

(2)如图14-3，小明同学说：“当点Q滑动到点H的位

置时，PQ与⊙O是相切的．”你认为他的判断对吗？

为什么？

(3)①小丽同学发现：“当点P运动到OH上时，点P到l

的距离最小．”事实上，还存在着点P到l距离最大

的位置，此时，点P到l的距离是　　　　 分米；

②当OP绕点O左右摆动时，所扫过的区域为扇形，

求这个扇形面积最大时圆心角的度数．

22．(本小题满分9分)

如图13，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C分别在坐标轴上，顶点B的坐标为(4，2)．过点D(0，3)和E(6，0)的直线分别与AB，BC交于点M，N．

(1)求直线DE的解析式和点M的坐标；

(2)若反比例函数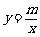(x＞0)的图象经过点M，求该反比例函数的解析式，并通过计算判断点N是否在该函数的图象上；

(3)若反比例函数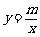(x＞0)的图象与△MNB有公共点，请直接写出m的取值范围．

21．(本小题满分9分)

(1)在图12-1中，“7分”所在扇形的圆心角

等于　　　　 °．

(2)请你将图12-2的统计图补充完整．

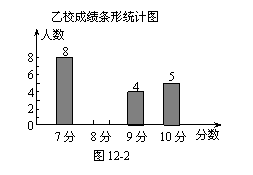(3)经计算，乙校的平均分是8.3分，中位数是8分，请写出甲校的平均分、中位数；并从平均分和中位数的角度分析哪个学校成绩较好．

(4)如果该教育局要组织8人的代表队参加市级团体赛，为便于管理，决定从这两所学校中的一所挑选参赛选手，请你分析，应选哪所学校？

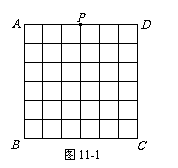
20．(本小题满分8分)如图11-1，正方形ABCD是一个6　×　6网格电子屏的示意图，其中每个小正方形的边长为1．位于AD中点处的光点P按图11-2的程序移动．

(1)请在图11-1中画出光点P经过的路径；

(2)求光点P经过的路径总长(结果保留π)．

19．(本小题满分8分)解方程：．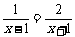

18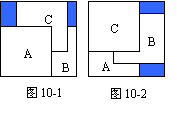．把三张大小相同的正方形卡片A，B，C叠放在一个底面为正方形的盒底上，底面未被卡片覆盖的部分用阴影表示．若按图10-1摆放时，阴影部分的面积为S₁；若按图10-2摆放时，阴影部分的面积为S₂，则S₁ 　　　　S₂(填“＞”、“＜”或“=”)．

17．某盏路灯照射的空间可以看成如图9所示的圆锥，它的高AO　=　8米，母线AB与底面半径OB的夹角为，，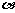

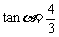则圆锥的底面积是　　　 平方米(结果保留π)．