
2. 开普勒第二定律:
1. 开普勒第一定律:
19,利用二次函数的图象求下列方程的近似根:(1)x2+x-12=0;(2)2x2-x-3=0.
20,已知抛物线与x轴交于点(1,0)和(2,0)且过点 (3,4).求抛物线的解析式.
21,已知二次函数y=x2-6x+8.求:
(1)抛物线与x轴和y轴相交的交点坐标;
(2)抛物线的顶点坐标;
(3)画出此抛物线图象,利用图象回答下列问题:
①方程x2-6x+8=0的解是什么?
②x取什么值时,函数值大于0?
③x取什么值时,函数值小于0?
22,当 x=4时,函数y=ax2+bx+c的最小值为-8,抛物线过点(6,0).求:
(1)顶点坐标和对称轴;
(2)函数的表达式;
(3)x取什么值时,y随x的增大而增大;x取什么值时,y随x增大而减小.
23,已知抛物线y=x2-2x-8.
(1)求证:该抛物线与x轴一定有两个交点;
(2)若该抛物线与x轴的两个交点分别为A、B,且它的顶点为P,求△ABP的面积.
24,如图5,宜昌西陵长江大桥属于抛物线形悬索桥,桥面(视为水平的)与主悬钢索之间用垂直钢拉索连接.桥两端主塔塔顶的海拔高度均是187.5米,桥的单孔跨度(即两主塔之间的距离)900米,这里水面的海拔高度是74米.若过主塔塔顶的主悬钢索(视为抛物线)最低点离桥面(视为直线)的高度为0.5米,桥面离水面的高度为19米.请你计算距离桥两端主塔100米处垂直钢拉索的长(结果精确到0.1米).
25,某通讯器材公司销售一种市场需求较大的新型通讯产品.已知每件产品的进价为40元,每年销售该种产品的总开支(不含进价)总计120万元.在销售过程中发现,年销售量y(万件)与销售单价x(元)之问存在着如图6所示的一次函数关系.
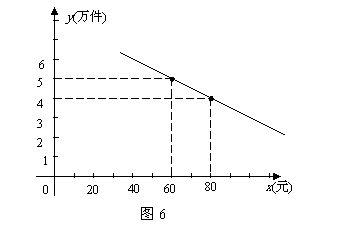

(1)求y关于x的函数关系式; (2)试写出该公司销售该种产品的年获利z(万元)关于销售单价x(元)的函数关系式(年获利=年销售额一年销售产品总进价一年总开支).当销售单价x为何值时,年获利最大?并求这个最大值; (3)若公司希望该种产品一年的销售获利不低于40万元,借助⑵中函数的图象,请你帮助该公司确定销售单价的范围.在此情况下,要使产品销售量最大,你认为销售单价应定为多少元?
26,(2008·东营市) 在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N.以MN为直径作⊙O,并在⊙O内作内接矩形AMPN.令AM=x.
(1)用含x的代数式表示△MNP的面积S;
(2)当x为何值时,⊙O与直线BC相切?
(3)在动点M的运动过程中,记△MNP与梯形BCNM重合的面积为y,试求y关于x的函数表达式,并求x为何值时,y的值最大,最大值是多少?



11,顶点为(-2,-5)且过点(1,-14)的抛物线的解析式为___.
12,若点A(2,m)在抛物线y=x2上,则点A关于y轴对称点的坐标是___.
13,二次函数y=2x2+bx+c的顶点坐标是(1,-2).则b=___,c=___.
14,已知二次函数y=ax2+bx+c (a≠0)与一次函数y=kx+m(k≠0)的图象相交于点A(-2,4),B(8,2),如图4所示,能使y1>y2成立的x取值范围是___.

15,小王利用计算机设计了一个计算程序,输入和输出的数据如下表:
|
输入 |
… |
1 |
2 |
3 |
4 |
5 |
… |
|
输出 |
… |
2 |
5 |
10 |
17 |
26 |
… |
若输入的数据是x时,输出的数据是y,y是x的二次函数,则y与x 的函数表达式为___.
16,平移抛物线y=x2+2x-8,使它经过原点,写出平移后抛物线的一个解析式___.
17,抛物线y=ax2+bx+c中,已知a∶b∶c=l∶2∶3,最小值为6,则此抛物线的解析式为___.
18,把一根长100cm的铁丝分为两部分,每一部分均弯曲成一个正方形,它们的面积和最小是___.
1,函数y=x2-4的图象与y轴的交点坐标是( )
A.(2,0) B.(-2,0) C.(0,4) D.(0,-4)
2,在平面直角坐标系中,抛物线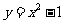 与
与 轴的交点的个数是( )
轴的交点的个数是( )
A.3 B.2 C.1 D.0
3,抛物线经过第一、三、四象限,则抛物线的顶点必在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4,二次函数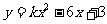 的图象与
的图象与 轴有交点,则
轴有交点,则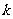 的取值范围是[ ]
的取值范围是[ ]
A.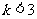 B.
B.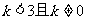 C.
C.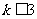 D.
D.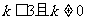
5,已知反比例函数y=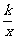 的图象在每个象限内y随x的增大而增大,则二次函数y=2kx2-x+k2的图象大致为如图2中的(
)
的图象在每个象限内y随x的增大而增大,则二次函数y=2kx2-x+k2的图象大致为如图2中的(
)

6,二次函数y=ax2+bx+c的图象如图3,则点(b,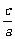 )在(
)
)在(
)
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7,某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长的百分数都是x,那么y与x的函数关系是( )
A.y=x2+a B.y=a(x-1)2 C.y=a(1-x)2 D.y=a(l+x)2
8,若二次函数y=ax2+bx+c,当x取x1,x2(x1≠x2)时,函数值相等,则当x取(x1+x2)时,函数值为( )
A.a+c B.a-c C.-c D.c
9,不论m为何实数,抛物线y=x2-mx+m-2( )
A.在x轴上方 B.与x轴只有一个交点 C.与x轴有两个交点 D.在x轴下方
10,若二次函数y=x2-x与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
A.这两个函数图象有相同的对称轴 B.这两个函数图象的开口方向相反
C.方程-x2+k=0没有实数根 D.二次函数y=-x2+k的最大值为
14.(15分)(2009·天津高考)2008年12月,天文学家们通过观测的数据确认了银河系中央的黑洞“人马座A*”的质量与太阳质量的倍数关系.研究发现,有一星体S2绕人马座A*做椭圆运动,其轨道半长轴为9.50×102天文单位(地球公转轨道的半径为一个天文单位),人马座A*就处在该椭圆的一个焦点上.观测得到S2星的运行周期为15.2年.
若将S2星的运行轨道视为半径r=9.50×102天文单位的圆轨道,试估算人马座A*的质量MA是太阳质量MS的多少倍(结果保留一位有效数字).
解析:S2星绕人马座A*做圆周运动的向心力由人马座A*对S2星的万有引力提供,设S2星的质量为mS2,角速度为ω,周期为T,则
G=mS2ω2r ①
ω= ②
设地球质量为mE,公转轨道半径为rE,周期为TE,则
G=mE()2rE ③
综合上述三式得=()3()2
式中TE=1年,rE=1天文单位
代入数据可得=4×106.
答案:4×106倍
()
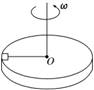
13.(15分)如图10所示,水平转盘上放有质量为m的物块,当物块
到转轴的距离为r时,连接物块和转轴的绳刚好被拉直(绳上张力 图10
为零).物块和转盘间最大静摩擦力是其正压力的μ倍.求:
(1)当转盘的角速度ω1= 时,细绳的拉力F1;
(2)当转盘的角速度ω2= 时,细绳的拉力F2.
解析:设角速度为ω0时,物块所受静摩擦力为最大静摩擦力,有
μmg=mω02r
得ω0=
(1)由于ω1= <ω0,故绳未拉紧,此时静摩擦力未达到最大值,F1=0.
(2)由于ω2=>ω0,故绳被拉紧,
由F2+μmg=mω22r
得F2=μmg.
答案:(1)0 (2)μmg
12.(13分)如图9所示,有一倾角为30°的光滑斜面,斜面长L为10 m,
一小球从斜面顶端以10 m/s的速度在斜面上沿水平方向抛出.求:
(g取10 m/s2)
(1)小球沿斜面滑到底端时的水平位移x; 图9
(2)小球到达斜面底端时的速度大小.
解析:(1)沿初速度方向:x=v0t ①
沿斜面向下:a=gsinα ②
L=at2 ③
联立①②③代入数据得:x=20 m.
(2)沿斜面向下:v⊥=at ④
则:v= ⑤
联立②③④⑤解得:
v=10 m/s=14.1 m/s.
答案:(1)20 m (2)14.1 m/s
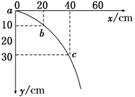
11.(8分)(2010·陕西省西安铁一中月考)某同学在做平抛运动实
 得出如图8所示的小球运动轨迹,a、b、c三点的位置在运
得出如图8所示的小球运动轨迹,a、b、c三点的位置在运
动轨迹上已标出.则:(g取10 m/s2)
(1)小球平抛的初速度为________ m/s.
(2)小球开始做平抛运动的位置坐标为________ cm. 图8
y=________ cm.
(3)小球运动到b点的速度为________ m/s.
解析:(1)小球由a到b,b到c,水平方向做匀速运动,时间间隔相同,竖直方向上做匀加速运动,则由Δy=gΔt2得出Δt=0.1 s.再根据水平方向的位移x=v0Δt,解得v0= m/s=2 m/s.
(2)小球在b点的竖直速度为v==1.5 m/s.由v=gt1得t1=0.15 s,则从抛物点到a点的时间为t2=0.15 s-0.1 s=0.05 s,水平初速度为2 m/s,从抛物点到a点的水平距离x=v0t2=2 m/s×0.05 s=0.1 m=10 cm,竖直距离y=gt22=0.012 5 m=1.25 cm,所以抛物点坐标为(-10,-1.25).
(3)小球运动到b点的速度为水平方向做匀速运动的速度2 m/s和竖直方向运动的速度1.5 m/s的矢量和,应为2.5 m/s.
答案:(1)2 (2)-10 -1.25 (3)2.5
10.(4分)(2010·潍坊质检)某同学利用如图7所示的两种装置探究平抛运动,方案如下:
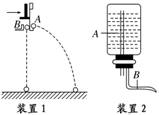
图7
装置1:用小锤打击金属片,A球水平抛出,同时B球自由下落.仔细观察A、B两球是否同时落到水平地面上.若同时落地,则说明水平分运动是匀速运动,竖直分运动是自由落体运动.
装置2:竖直管A上端要高于水面,这样可在较长时间内得到稳定的细水柱.水平管B喷出水流,在紧靠水流、平行于水流的玻璃板上用彩笔描出水流的轨迹,这就是平抛运动的轨迹.
找出以上叙述中不当之处并写到下面:
(1)__ ____________________________________________________________________;
(2)______________________________________________________________________.
解析:(1)若同时落地,不能说明水平分运动是匀速运动,只能说明竖直方向为自由落体运动.
(2)竖直管A上端要高于水面(应低于).
答案:见解析
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com