
10.将质量M=3m的木块固定在水平面上,一颗质量为m的子弹以速度v0沿水平方向射入木块,子弹穿出木块时的速度为;现将同样的木块放在光滑的水平面上,相同的子弹仍以速度v0沿水平方向射入木块,则子弹( )
 A.不能射穿木块,子弹和木块以相同的速度做匀速运动
A.不能射穿木块,子弹和木块以相同的速度做匀速运动
B.能射穿木块
C.刚好能射穿木块,子弹射穿木块时速度为零
D.刚好能射穿木块,子弹射穿木块时速度大于
解析:当木块固定时,由动能定理及能量的转化和守恒定律知:
Wf=Q=mv-m()2=mv
假设木块置于光滑水平面时,子弹射穿至木块右端时恰好与木块达到的共同速度,由动量守恒定律得:
mv0=(m+M)v1
解得:v1=
则射穿后子弹与木块的总动能以及射穿过程摩擦生热和为:
E′=·(4m)·()2+mv=mv>mv
这违背了能量的转化和守恒定律,故子弹不可能射穿木块.
答案:A
非选择题部分共3小题,共40分.
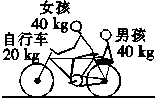
9.如图所示,质量相同的两小球A、B均用细线吊在天花板上(A、B两球均不触地).现将小球A拉离平衡位置,使其从高h处由静止开始向下摆动,当它摆至最低点时,恰好与小球B正碰,则碰后B球能升起的高度可能为( )
A. B.h C. D.
解析:当两球发生弹性碰撞时,B球能向左摆至的最大高度hmax=h
当两球发生完全非弹性碰撞时,B球能向左摆至的高度有最小极值hmin,有:
m=2mv
v2=2ghmin
可得:hmin=
故B球能向左摆的高度h′的范围为:≤h′≤h.
答案:ABC
8.  如图所示,两物体A、B用轻质弹簧相连静止在光滑的水平面上,现同时对A、B两物体施加等大、反向的水平恒力F1、F2,使A、B同时由静止开始运动.在运动过程中,对A、B两物体及弹簧组成的系统,下列说法正确的是(整个过程中弹簧不超过其弹性限度)( )
如图所示,两物体A、B用轻质弹簧相连静止在光滑的水平面上,现同时对A、B两物体施加等大、反向的水平恒力F1、F2,使A、B同时由静止开始运动.在运动过程中,对A、B两物体及弹簧组成的系统,下列说法正确的是(整个过程中弹簧不超过其弹性限度)( )
A.动量始终守恒
B.机械能始终守恒
C.当弹簧伸长到最长时,系统的机械能最大
D.当弹力的大小与F1、F2的大小相等时,A、B两物体的速度为零
 解析:A、B及弹簧组成的系统所受的合外力为零,则动量始终守恒,选项A正确;F1、F2对A、B同时做正功或负功,系统的机械能不守恒,选项B错误;因为F1、F2对系统做功之和等于系统机械能的变化,故在弹簧伸长的过程中机械能一直增大,选项C正确;当弹力的大小与F1、F2的大小相等时,A、B的速度最大,选项D错误.
解析:A、B及弹簧组成的系统所受的合外力为零,则动量始终守恒,选项A正确;F1、F2对A、B同时做正功或负功,系统的机械能不守恒,选项B错误;因为F1、F2对系统做功之和等于系统机械能的变化,故在弹簧伸长的过程中机械能一直增大,选项C正确;当弹力的大小与F1、F2的大小相等时,A、B的速度最大,选项D错误.
答案:AC
7.如图所示,一木板静止在光滑水平面上,其右端有一根轻质弹簧沿水平方向与木板相连,木板的质量M=3 kg.一质量m=1 kg的铁块以水平速度v0=4 m/s从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.在上述过程中,弹簧具有的最大弹性势能为( )
A.3 J B.6 J C.20 J D.4 J
 解析:由动量守恒定律有:mv0=(m+M)vt
解析:由动量守恒定律有:mv0=(m+M)vt
由题意知,系统由于摩擦生热而损失的动能为:
ΔEk=mv-(m+M)v=6 J
故知弹簧压缩最大时摩擦生热损失的动能为:
ΔEk=3 J
此时弹簧的弹性势能最大为:
Ep=mv-ΔEk-(m+M)v=3 J.
答案:A
6. 如图所示,船的质量为M,船上站一质量为m的运动员,运动员要从这静止的船上水平跃出,到达与船水平距离为s、比甲板低h的岸上,至少要做功W,不计水的阻力,则下列说法正确的是( )
如图所示,船的质量为M,船上站一质量为m的运动员,运动员要从这静止的船上水平跃出,到达与船水平距离为s、比甲板低h的岸上,至少要做功W,不计水的阻力,则下列说法正确的是( )
A.如s、h一定,M越大,W越大
B.如s、m和h一定,M越大,W越小
C.如s、M和h一定,W与m成正比
D.如s、m和M一定,h越大,W越小
解析:设运动员要跳上岸所需的最小初速度为v1,此时船的反冲速度为v2,由动量守恒定律有:
Mv2=mv1=p0
其中v1=s
可得:v2=
由能量的转化和守恒定律知,运动员做的功为:
W=Mv+mv=(+).
答案:BD
5. 如图所示,在光滑水平面上的小车的表面由光滑的弧形段AB和粗糙的水平段BC组成.当小车固定时,从A点由静止滑下的物体到C点恰好停止.如果小车不固定,物体仍从A点静止滑下,则( )
如图所示,在光滑水平面上的小车的表面由光滑的弧形段AB和粗糙的水平段BC组成.当小车固定时,从A点由静止滑下的物体到C点恰好停止.如果小车不固定,物体仍从A点静止滑下,则( )
A.还是滑到C点停止
B.滑到BC间某处停止
C.会冲出C点落到车外
D.上述三种情况都有可能
解析:由动量守恒定律知,小车不固定时,物体与小车达到的共同速度也为零,又由能量的转化和守恒定律有:
mg·Δh=μmg·ΔL
即物体仍将滑至C点停住.
答案:A
4.2002年,美国《科学》杂志评出的“2001年世界十大科技突破”中,有一项是加拿大萨德伯里中微子观测站的成果.该站揭示了中微子失踪的原因.即观测到的中微子数目比理论值少是因为部分中微子在运动过程中转化为一个μ子和一个τ子.在上述研究中有以下说法,其中正确的是( )
A.该研究过程中牛顿第二定律依然适用
B.该研究过程中能量转化和守恒定律依然适用
C.若发现μ子和中微子的运动方向一致,则τ子的运动方向与中微子的运动方向也可能一致
D.若发现μ子和中微子的运动方向相反,则τ子的运动方向与中微子的运动方向也可能相反
解析:牛顿第二定律不适用于微观高速的物理过程,而能量的转化和守恒定律依然适用,故选项A错误、B正确.
由动量守恒定律可得:mcv0=mμv1+mτv2
若v1与v0同向,则v2可能与v0同向,也可能反向;若v1与v0反向,则v2一定与v0同向,选项C正确、D错误.
答案:BC
3.如图甲所示,长木板A静止在光滑的水平面上,质量m=2 kg的物体B以v0=2 m/s的水平速度滑上A的表面,由于A、B间存在摩擦,之后A、B速度随时间变化情况如图乙所示,则下列说法中正确的是( )
A.木板获得的动能为1 J
B.系统损失的机械能为2 J
C.木板A的最小长度为1 m
D.A、B间的动摩擦因数为0.2
解析:由图线知A、B的共同速度为v=1 m/s,由动量守恒定律有:
mBv0=(mA+mB)v
可得:mA=2 kg,Ek=mAv2=1 J
ΔE=mBv-(mA+mB)v2=2 J
A的最小长度为AB相对滑动的位移,由图象可得:
Δs=1 m
又因为μmg·Δs=ΔE,可得:μ=0.1.
答案:ABC
2. 如图所示,一小车放在光滑水平面上,A端固定一个轻弹簧,B端粘有油泥,小车的总质量为M,一质量为m的木块C放在小车上,用细绳固定使弹簧处于压缩状态.开始时小车和C都静止;现突然烧断细绳,C被释放,使C离开弹簧向B端冲去并跟B端油泥粘在一起,忽略一切摩擦,以下说法正确的是( )
如图所示,一小车放在光滑水平面上,A端固定一个轻弹簧,B端粘有油泥,小车的总质量为M,一质量为m的木块C放在小车上,用细绳固定使弹簧处于压缩状态.开始时小车和C都静止;现突然烧断细绳,C被释放,使C离开弹簧向B端冲去并跟B端油泥粘在一起,忽略一切摩擦,以下说法正确的是( )
A.弹簧伸长过程中C向右运动,同时小车也向右运动
B.C与B碰前,C与小车的速率之比为m∶M
C.C与油泥粘在一起后,小车立即停止运动
D.C与油泥粘在一起后,小车继续向右运动
解析:小车和木块组成的系统动量守恒,C向右运动时小车向左运动,且有:
mv=Mv′
即v∶v′=M∶m,选项A、B错误;
 由动量守恒定律知,系统的总动量始终为零,故C与油泥粘一起后与小车的共同速度立即变为零,选项C正确.
由动量守恒定律知,系统的总动量始终为零,故C与油泥粘一起后与小车的共同速度立即变为零,选项C正确.
答案:C
1. 如图所示,两带电的金属球在绝缘的光滑水平面上沿同一直线相向运动,A带电荷量为-q,B带电荷量为+2q,下列说法正确的是( )
如图所示,两带电的金属球在绝缘的光滑水平面上沿同一直线相向运动,A带电荷量为-q,B带电荷量为+2q,下列说法正确的是( )
A.相碰前两球运动中动量不守恒
B.相碰前两球的总动量随距离的减小而增大
C.两球相碰分离后的总动量不等于相碰前的总动量,因为碰前作用力为引力,碰后为斥力
D.两球相碰分离后的总动量等于碰前的总动量,因为两球组成的系统合外力为零
解析:碰撞前后整个过程动量守恒,选项A、B、C错误,D正确.
答案:D
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com