5.如图所示，人在平板车上用水平恒力拉绳使重物能逐渐靠近自己，人相对车始终不动，重物与平板车之间、平板车与地面之间均无摩擦.设开始拉重物时车和重物都是静止的，车和人的总质量M＝100 kg ，重物的质量m＝50 kg，拉力F＝200 N，重物在车上向人靠近了3 m，求：

(1)车在地面上移动的距离.

(2)这时车和重物的速度.

解析：(1)设重物在车上向人靠近L＝3 m时，车在地面上移动的距离为s，依题意有：

m(L－s)＝Ms

整理得：s＝1 m.

(2)人和车的加速度a＝＝ m/s²＝2 m/s²

则人和车在地面上移动1 m时的速度为：

v＝＝2 m/s

此时物体的对地速度为v_物，根据mv_物＝Mv得：

v_物＝4 m/s.

答案：(1)1 m　(2)4 m/s

4.小球1追碰小球2，碰撞前两球的动量分别为p₁＝5 kg·m/s，p₂＝7 kg·m/s，正碰后小球2的动量p₂′＝10 kg·m/s.则两球的质量关系可能是(　)

A.m₂＝m₁　　　B.m₂＝2m₁

C.m₂＝4m₁　 D.m₂＝6m₁

解析：由动量守恒定律，很容易得到碰后小球1的动量p₁′＝2 kg·m/s，这丝毫不能反映出两球的质量关系，这就要从题中内含的其他关系去寻找.

首先，“追碰”表明碰前小球1的速度大于小球2的速度，即v₁＞v₂，由v＝可得，＞，即m₂＞，排除了选项A的可能.

按同样思路，碰后应有v₁′≤v₂′，≤，有m₂≤5m₁，排除了选项D的可能.

由动能不增原则可知：E_k1+E_k2≥E_k1′+E_k2′，由动能E_k与动量p的关系：E_k＝

可得：+≥+

即有：m₂≥，排除了选项B的可能.

综合以上结论得：≤m₂≤5m₁，只有选项C正确.

答案：C

3.A、B两球在光滑水平面上相向运动，已知m_A＞m_B，当两球相碰后，其中一球停止运动，则可断定(　)

A.碰前A的动量与B的动量大小相等

B.碰前A的动量大于B的动量

C.若碰后A的速度为零，则碰前A的动量大于B的动量

D.若碰后B的速度为零，则碰前A的动量大于B的动量

解析：碰后只有一球静止，说明系统总动量不为零，选项A错误；由于不知道哪个球停止，则不能判断碰前谁的动量大，B错误；由于二球相向运动，一球停止，另一球的运动方向必与其原运动方向反向，总动量与静止球原动量方向相同，因此选项C正确.

答案：C

2.质量为M的木块放在光滑的水平桌面上处于静止状态，今有一颗质量为m、速度为v₀的子弹沿水平方向击中木块，在子弹未穿出木块的过程中，木块受到的冲量大小为(　)

A.mv₀　　　　B.mv₀－

C.　 D.mv₀－

解析：由动量守恒定律得：mv₀＝(m+M)v

木块受到的冲量大小I＝Mv

联立解得：I＝

选项C、D是相同结果的不同表达式，所以选项C、D正确.

答案：CD

1.如图所示，木块B与水平弹簧相连放在光滑水平面上，子弹A沿水平方向射入木块后留在木块B内，入射时间极短，关于子弹和木块组成的系统，下列说法正确的是(　)

A.子弹从开始射入木块到弹簧压缩到最短的过程中，系统动量守恒

B.子弹射入木块的过程中，系统动量守恒

C.子弹射入木块的过程中，系统动量不守恒

D.木块压缩弹簧的过程中，系统动量守恒

解析：子弹射入木块在瞬间完成，这一过程木块的位移以及弹簧的作用可以忽略不计，故木块与子弹组成的系统动量守恒，这一过程机械能不守恒.压缩弹簧的过程动量越来越小，但木块和弹簧组成的系统机械能守恒，选项B正确.

答案：B

12.光滑水平面上放着质量m_A＝1 kg的物块A与质量m_B＝2 kg的物块B，A与B均可视为质点，A靠在竖直墙壁上，A、B间夹一个被压缩的轻弹簧(弹簧与A、B均不拴接)，用手挡住B不动，此时弹簧弹性势能E_p＝49 J.在A、B间系一轻质细绳，细绳长度大于弹簧的自然长度，如图所示.放手后B向右运动，绳在短暂时间内被拉断，之后B冲上与水平面相切的竖直半圆光滑轨道，其半径R＝0.5 m，B恰能到达最高点C.取g＝10 m/s²，求：

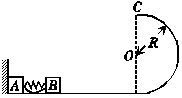(1)绳拉断后瞬间B的速度v_B的大小；

(2)绳拉断过程绳对B的冲量I的大小；

(3)绳拉断过程绳对A所做的功W.[2008年高考·天津理综卷]

　分析：A、B系统的运动可以分为以下过程：

(1)弹簧推B物体至绳子伸直前；

(2)绳子伸直至被拉断；

(3)B运行至最高点过程.

分析清物体的运动过程，问题就变得很清晰了.

解析：(1)设B在绳被拉断后瞬间的速度为v_B，到达C点时的速度为v_C，有：

m_Bg＝m_B

m_Bv＝m_Bv+2m_BgR

代入数据得：v_B＝5 m/s.

(2)设弹簧恢复到自然长度时B的速度为v₁，取水平向右为正方向，有：

E_p＝m_Bv

I＝m_Bv_B－m_Bv₁

代入数据得：I＝－4 N·s，其大小为4 N·s.

(3)设绳断后A的速度为v_A，取水平向右为正方向，有：

m_Bv₁＝m_Bv_B+m_Av_A

W＝m_Av

代入数据得：W＝8 J.

答案：(1)5 m/s　(2)4 N·s　(3)8 J

11.用放射源钋的α射线轰击铍时，能放出一种穿透力极强的中性射线，这就是所谓的铍“辐射”.1932年，查德威克用铍“辐射”分别照射(轰击)氢和氮(它们可视为处于静止状态)，测得照射后沿铍“辐射”方向高速运动的氢核、氮核的速度之比为7∶1.查德威克假设铍“辐射”是由一种质量不为零的中性粒子构成的，从而通过上述实验在历史上首次发现了中子.假设铍“辐射”中的中性粒子与氢核或氮核发生弹性正碰，试在不考虑相对论效应条件下计算构成铍“辐射”的中性粒子的质量.(质量用原子质量单位u表示，1 u等于一个¹²C原子质量的.取氢核和氮核的质量分别为1.0 u和14 u)[2007年高考·全国理综卷Ⅱ]

解析：设构成铍“辐射”的中性粒子的质量和速度分别为m和v，氢核的质量为m_H，构成铍“辐射”的中性粒子与氢核发生弹性正碰，碰后两粒子的速度分别为v′和v_H′.

由动量守恒和能量守恒定律得：

mv＝mv′+m_Hv_H′

mv²＝mv′²+m_Hv_H′²

解得：v_H′＝

同理，对质量为m_N的氮核，其碰后速度为：

v_N′＝

可得：m＝

根据题意可知：v_H′＝7v_N′

将数据代入可得：m＝1.2 u.

答案：1.2 u

10.如图甲所示，在光滑绝缘水平面的AB区域内存在水平向右的电场，电场强度E随时间的变化如图乙所示.不带电的绝缘小球P₂静止在O点.t＝0时，带正电的小球P₁以速度v₀从A点进入AB区域，随后与P₂发生正碰后反弹，反弹速度大小是碰前的倍，P₁的质量为m₁，带电荷量为q，P₂的质量m₂＝5m₁，A、O间距为L₀，O、B间距L＝.已知＝，T＝.

(1)求碰撞后小球P₁向左运动的最大距离及所需时间.

(2)讨论两球能否在OB区间内再次发生碰撞.

[2008年高考·广东物理卷]

解析：(1)小球P₁到达O点的时间t₁＝＝T，与P₂碰撞时，电场刚好由零增加到E₀.

设P₁、P₂碰撞后，P₂的速度为v₂，由动量守恒定律有：

m₁v₀＝m₁v₁+m₂v₂

其中v₁＝－v₀

解得：v₂＝(水平向右)

碰撞后小球P₁向左运动的最大距离s_m＝

又a₁＝＝

解得：s_m＝

所需时间t₂＝＝.

(2)设P₁、P₂碰撞后又经Δt时间在OB区间内再次发生碰撞，且P₁受到的电场力不变，由运动学公式，以水平向右为正方向，则有：

s₁＝s₂

即－v₁·Δt+a₁·Δt²＝v₂·Δt

解得：Δt＝＝3T

故P₁受到的电场力不变

对P₂分析：s₂＝v₂·Δt＝v₀·＝L₀<L＝

所以假设成立，两球能在OB区间内再次发生碰撞.

答案：(1)　

(2)两球能在OB区间内再次发生碰撞

9.一置于桌面上的质量为M的玩具炮可水平发射质量为m的炮弹，且炮可在水平方向自由移动.当炮身上未放置其他重物时，炮弹可击中水平地面上的目标A；当炮身上固定一质量为M₀的重物时，在原发射位置沿同一方向发射的炮弹可击中水平地面上的目标B.炮口离水平地面的高度为h.如果两次发射时“火药”提供的机械能相等，求B、A两目标与炮弹发射点之间的水平距离之比.[2008年高考·海南物理卷]

解析：由动量守恒定律和能量守恒定律得：

0＝mv₁－Mv₂

E＝mv+Mv

解得：v₁＝

炮弹射出后做平抛运动，故有：

h＝gt²

x＝v₁t

解得：目标A距炮口的水平距离x＝

同理，目标B距炮口的水平距离为：

x′＝

解得：＝.

答案：

8.

某同学利用如图所示的装置来验证动量守恒定律.图中两摆的摆长相同，且悬挂于同一高度处，A、B两摆球均很小，质量之比为1∶2.当两摆均处于自由静止状态时，其侧面刚好接触.向右上方拉动B球使其摆线伸直并与竖直方向成45°角，然后将其由静止释放.结果观察到两摆球粘在一起摆动，且最大摆角为30°.若本实验允许的最大误差为±4%，则此实验是否成功地验证了动量守恒定律？试分析说明理由.[2008年高考·宁夏理综卷]

解析：设摆球A、B的质量分别为m_A、m_B，摆长为l，B球的初始高度为h₁，碰撞前B球的速度为v_B.在不考虑摆线的质量的情况下，根据题意及机械能守恒定律得：

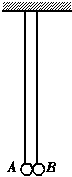h₁＝l(1－cos 45°)

m_Bv＝m_Bgh₁

设碰撞前后两摆球的总动量的大小分别为p₁、p₂，则有：

p₁＝m_Bv_B

联立解得：p₁＝m_B

同理可得：p₂＝(m_A+m_B)

联立解得：＝

解得：()²＝1.03

由此可以推出：||≈2%＜4%

所以，此实验在规定的范围内验证了动量守恒定律.

答案：是　理由是：实验的误差约为2%，小于允许的最大误差