2.如图所示，一个直角支架AOB的AO部分水平放置，表面粗糙；OB部分竖直向下，表面光滑.AO上套有小环P，OB上套有小环Q，两环的质量均为m，两环由一根质量可忽略、不可伸长的细绳相连，并在某一位置平衡.现将P环向左移一小段距离，两环再次达到平衡.那么将移动后的平衡状态和原来的平衡状态比较，AO杆对P环的支持力FN和摩擦力f的变化情况是(　)

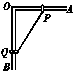A.FN不变，f变大　 B.FN不变，f变小

C.FN变大，f变大　 D.FN变大，f变小

解析：用隔离法分析Q，因OB杆光滑，所以绳拉力F的竖直分力等于Q环的重力，即Fcos α＝mg，式中α表示绳与OB的夹角.当P向左平移一段距离后，α变小，由F＝知，拉力F变小.对P环有f＝Fsin α，可知f变小.

用整体法分析P、Q，其所受的外力有：重力2mg、OB杆对Q环的水平向左的弹力FB、OA杆对P环竖直向上的支持力FN和水平向右的摩擦力f.根据竖直方向平衡知，FN恒等于2mg.所以，正确选项为B.

答案：B

1.如图所示，A、B两物体的重力分别是GA＝2 N、GB＝4 N，A、B之间用轻直杆连接，A用轻弹簧悬挂在顶板上.已知弹簧的弹力大小F＝3 N，则轻杆内部的弹力以及B对地面的压力的可能值分别是(　)

A.5 N和9 N　　　B.2 N和5 N

C.1 N和6 N　 D.2 N和3 N

解析：当弹簧处于压缩状态时，有：

FT＝F+GA＝5 N，FN＝F+GA+GB＝9 N

当弹簧处于伸长状态时，有：

FT′＝F－GA＝1 N，FN′＝GA+GB－F＝3 N.

答案：A

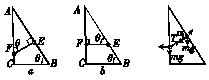
6.如图甲所示，用光滑的金属杆做的直角三角形框ABC的AB边和AC边上各有一完全相同的小环E和F，用一根细线把E、F连接起来，细线比BC边短，使三角形竖直放置，BC边水平.若已知AB边与BC边的夹角θ＝60°，求两环平衡时细线与AB边的夹角α.

解析：平衡时每个小环都受重力、金属杆的弹力和细线拉力的作用.如图乙所示，若α≤θ，容易判断F不可能平衡；若α≥，则容易判断E不能平衡，故α的大小应大于60°而小于90°.现分别画出E、F的受力示意图如图丙所示.

对于E，由平衡条件可得：mgcos 30°＝Tcos α

对于F，由平衡条件可得：mg＝Tcos (150°－α)

解得：tan α＝

即平衡时细线与AB边的夹角α＝arctan.

答案：arctan

金典练习二　力的合成和分解　共点力平衡　受力分析

选择题部分共10小题，每小题6分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

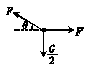
5.如图甲所示，重为G的均匀链条，两端用等长的轻绳连接挂在等高的

地方，绳与水平方向成θ角.试求：

(1)绳子的张力.

(2)链条最低点的张力.

解析：在求链条两端的张力时，可把链条当做一个质点处理，由于两边具有对称性，两端点的拉力大小相等，受力情况如图乙所示.

取链条整体为研究对象.

(1)由平衡条件知，在竖直方向：2Fsin θ＝G

得：绳对链条两端的拉力F＝.

(2)在求链条最低点的张力时，可将链条一分为二，取一半研究.受力情况如丙所示.由平衡条件知，在水平方向：F′＝Fcos θ＝cot θ.

答案：(1)　(2)cot θ

4.如图甲所示，竖直放置的轻弹簧一端固定在地面上，另一端与斜面体P连接，P与斜放的固定挡板MN接触且处于静止状态，弹簧处于竖直方向，则斜面体P此刻受到外力的个数可能为(　)

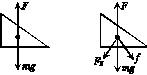
A.2　　B.3　　C.4　　D.5

解析：当弹簧的弹力大小等于斜块的重力时，P受2个力的作用；当弹簧弹力大于P受的重力时，受4个力作用，受力示意图分别如图乙所示.答案：AC

3.如图甲所示，轻杆插入墙中，轻绳绕过杆末端的定滑轮悬挂一重物，另一端由墙上A点逐渐上移.下列关于绳上的张力和轻杆对滑轮的弹力的叙述中，正确的是(　)

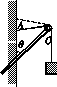A.绳的张力与杆的弹力均减小

B.绳的张力先减小后增大，杆的弹力一直减小

C.绳的张力先增大后减小，杆的弹力一直增大

D.绳的张力保持不变，杆的弹力一直减小

解析：绕过滑轮的轻绳张力处处相等，

大小等于重物的重力，故A点上移时绳的张力不变.

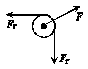再取滑轮及与其接触的轻绳为研究对象，其受力情况如图乙所示.

由平衡条件知，轻杆对滑轮的弹力与两侧绳的拉力的合力大小相等、方向相反，故A点上移时，两侧绳拉力的夹角增大，轻杆的弹力减小，选项D正确.

答案：D

2.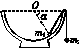如图甲所示，一个半球形碗放在桌面上，碗口水平，O点为其球心，碗的内表面及碗口都是光滑的.一根细线跨在碗口上，线的两端分别系有质量为m1和m2的小球，当它们处于平衡状态时，质量为m1的小球与O点的连线与水平方向的夹角α＝60°，则两个小球的质量之比 为(　)

A.　　B.　　C.　　D.

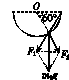解析：方法一　分解法

将球m1的重力分解，作出力的示意图，如图乙所示，由题意知，作出的平行四边形为一菱形，则绳中张力为：F2＝

对球m2，绳中张力F1＝m2g

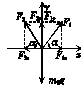解得：＝.

方法二　正交分解法

将m1所受的绳的拉力F1和碗的支持力F2正交分解，如图丙所示.

在x轴上：F1cos α＝F2cos α

在y轴上：F1sin α+F2sin α＝m1g

又F1＝m2g，α＝60°

联立解得：＝.

答案：A

5.如图甲所示，AOB为水平放置的光滑杆，∠AOB＝60°，AO、BO杆上套有两个质量不计的小环，两环间连有可伸缩的弹性绳.今从绳的中点处以沿∠AOB的角平分线且水平向右的力F缓慢地拉绳，待两环达到稳定状态时，求绳对环的拉力FT的大小.

解析：小环受到重力G、

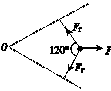绳的拉力FT和杆的弹力FN的作用，其中重力和弹力都与杆垂直，当绳的拉力也与杆垂直时小环才能平衡，故小环平衡时绳的中点处的受力情况如图乙所示.由绳的张力的特点可知，绳对环的拉力FT的大小为F.

答案：F

第4讲　共点力平衡　受力分析

体验成功

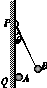　1.如图甲所示，竖直绝缘墙壁上的Q处有一固定的质点A，Q正上方的P点处固定一细线，细线另一端悬挂质点B， A、B两质点因为带电而相互排斥，致使悬线与竖直方向成θ角.由于漏电使A、B两质点的带电荷量逐渐减小，在电荷漏完之前悬线对悬点P的拉力大小将(　)

A.保持不变　　　B.先变大后变小

C.逐渐减小　 D.逐渐增大

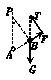解析：小球B的受力情况如图乙所示，三个力构成的矢量三角形与△BPA相似，根据相似比有：

＝

故T保持不变.

答案：A

4.如图甲所示，用轻弹簧竖直悬挂一质量为m的物体，静止时该弹簧的伸长量为L0.现用该弹簧沿斜面方向拉住质量为3m的物体，静止时弹簧的伸长量也为L0，已知斜面的倾角为30°，则物体所受到的摩擦力(　)

A.等于零

B.大小为mg，方向沿斜面向下

C.大小为mg，方向沿斜面向上

D.大小为mg，方向沿斜面向上

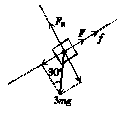解析：弹簧沿斜面拉物体时，

弹力的大小F＝kL0＝mg，故物体的受力情况如图乙所示.物体受到摩擦力的大小为：

f＝3mgsin 30°－F＝mg，方向沿斜面向上.

答案：C

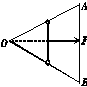
3.如图甲所示，水平地面上固定着一竖直立柱，某人通过柱顶的定滑轮拉着绳的一端将200 N的重物拉住不动.已知绳与水平地面的夹角为30°，则定滑轮所受绳的压力大小为(　)

A.400 N　　　　B.200 N

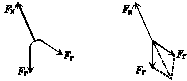C.300 N　 D.200 N

解析：定滑轮受到与其接触的绳子的弹力，取这段绳子为研究对象，其受力情况如图乙所示

由平衡条件得：FN′＝2FT·cos 30°＝200 N

又由牛顿第三定律得：

绳对滑轮的压力FN＝FN′＝200 N.

答案：B