5.如图所示，一根轻杆长为2L，中点A和右端点B各固定一个小球，m_B＝2m_A左端O为光滑水平转轴.开始时杆静止在水平位置，释放后将向下摆动至竖直，在此过程中以下说法正确的是(　)

A.A、B两球的机械能都守恒

B.A、B两球的机械能不守恒，但它们组成的系统机械能守恒

C.这一过程O、A间轻杆对A球做正功

D.这一过程A、B间轻杆对A球做正功

解析：两小球及轻杆组成的系统的机械能守恒，设摆到竖直时角速度为ω，有：

m(Lω)²+·2m(2Lω)²＝mgL+2mg·2L

解得：ω＝

即A的动能E_kA＝m(ωL)²＝mgL＜|ΔE_pA|

B的动能E_kB＝·2m(ω·2L)²

＝·2mg·2L＞|ΔE_pB|

故选项A错误、B正确.

又因为下摆的过程O、A间轻杆的弹力沿杆方向不做功，故知A、B之间轻杆对A球做负功.

答案：B

4.用平行于斜面向下的拉力F将一个物体沿斜面往下拉动后，拉力的大小等于摩擦力，则

A.物体做匀速运动

B.合外力对物体做功等于零

C.物体的机械能减少

D.物体的机械能不变

解析：物体所受的力中，重力、拉力、摩擦力对物体做功，拉力与摩擦力做的功相互抵消，重力做功不影响机械能，故物体的机械能不变.

答案：D

3.如图所示，长为L的轻杆一段固定一质量为m的小球，另一端安装有固定转动轴O，杆可在竖直平面内绕O无摩擦转动.若在最低点P处给小球一沿切线方向的初速度v₀＝2，不计空气阻力，则下列说法正确的是(　)

A.小球不可能到达圆周轨道的最高点Q

B.小球能达到圆周轨道的最高点Q，且在Q点受到轻杆向上的支持力

C.小球能到达圆周轨道的最高点Q，且在Q点受到轻杆向下的拉力

D.小球能达到圆周轨道的最高点Q，且在Q点恰好不受轻杆的弹力

解析：设小球能到达Q点，且到达Q点时具有速度v，由机械能守恒得：

mv＝mg·2L+mv²

可解得：v＝0

在最高点，小球所需的向心力为零，故受轻杆向上的大小为mg的支持力.

答案：B

2.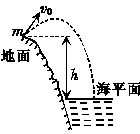如图所示，在地面上以速度v₀抛出质量为m的物体，抛出后物体落到比地面低h的海平面上.若以地面为零势能面且不计空气阻力，则下列说法中不正确的是(　)

A.物体到海平面时的重力势能为mgh

B.重力对物体做的功为mgh

C.物体在海平面上的动能为mv+mgh

D.物体在海平面上的机械能为mv

解析：以地面为参考平面，物体在海平面时的重力势能为－mgh，故A错误；抛出后的过程中机械能守恒，所以C、D正确；重力做功与路径无关，所以B正确.

答案：A

1.质量为m的物体由静止开始以2g的加速度竖直向下运动h高度.下列说法中正确的是(　)

A.物体的势能减少2mgh　B.物体的机械能保持不变

C.物体的动能增加2mgh　 D.物体的机械能增加mgh

解析：重力势能的减少量等于重力做的功，即ΔE_p＝mgh，A错误.

由题意知，物体除受重力外还受大小为mg的向下的作用力，机械能不守恒，B错误.

物体的合外力F_合＝2mg，故其动能的增量ΔE_k＝2mgh，C正确.

ΔE_p＝－mgh，ΔE_k＝2mgh，故ΔE＝ΔE_k+ΔE_p＝mgh，D正确.

答案：CD

13.(14分)湖面上一点O上下振动，振幅为0.2 m，以O点为圆心形成圆形水波，如图甲所示，A、B、O三点在一条直线上，OA间的距离为4.0 m，OB间的距离为2.4 m.某时刻O点处在波峰位置，观察发现2 s后此波峰传到A点，此时O点正通过平衡位置向下运动，OA间还有一个波峰.将水波近似为简谐波.

(1)求此水波的传播速度、周期和波长.

(2)以O点处在波峰位置为0时刻，某同学打算根据OB间的距离与波长的关系，确定B点在0时刻的振动情况，画出B点的振动图象.你认为该同学的思路是否可行？若可行，画出B点振动图象，若不可行，请给出正确思路并画出B点的振动图象.[2007年高考·山东理综卷]

解析：(1)由题意可知，v＝＝2 m/s

Δt＝·T，即T＝1.6 s

λ＝vT＝3.2 m.

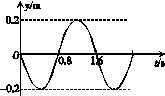
(2)可行.振动图象如图乙所示.

答案：(1)2 m/s　1.6 s　3.2 m

(2)可行.振动图象如图乙所示.

12.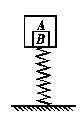(13分)一劲度系数k＝400 N/m的轻弹簧直立在地面上，弹簧的上端与盒子A连接在一起，盒子内装有物体B，B的下表面恰与盒子接触，如图所示.已知A和B的质量m_A＝m_B＝1 kg，g＝10 m/s²，不计阻力，先将A向上抬高使弹簧伸长5 cm 后从静止释放，A和B一起做上下方向的简谐运动.试求：

(1)A的振幅.

(2)A、B处于最高点和最低点时A对B的作用力大小.

解析：(1)当A、B处于平衡位置时弹簧的压缩量x₀＝＝0.02 m，将A抬高使弹簧伸长5 cm后释放，由简谐运动的对称性知振子的振幅A＝x₀+5 cm＝7 cm.

(2)当A、B位于最高点时，A、B的加速度大小为：

a＝＝20 m/s²，方向竖直向下.

对于B有：F_N1+m_Bg＝m_Ba

解得：A对B的弹力F_N1＝10 N，方向竖直向下

当A、B位于最低点时，由简谐运动的对称性知加速度大小也为a＝20 m/s²，方向竖直向上

对于B有：F_N2－m_Bg＝m_Ba.

解得：A对B的弹力F_N2＝30 N，方向竖直向上.

答案：(1)7 cm　(2)10 N　30 N

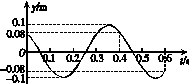
11.(13分)图甲为沿x轴向右传播的简谐横波在t＝1.2 s 时的波形图象，位于坐标原点处的观察者测到在4 s内有10个完整的波经过该点.

(1)求该波的波幅、频率、周期和波速.

(2)画出平衡位置在x轴上P点处的质点在0-0.6 s内的振动图象.

甲

　解析：(1)由题意可知A＝0.1 m

f＝＝2.5 Hz

T＝＝0.4 s

v＝λf＝5 m/s.

(2)P点处的质量在0-0.6 s内的振动图象，如图乙所示. 　　　　　　　　　　乙

答案：(1)0.1 m　2.5 Hz　0.4 s　5 m/s

(2)如图乙所示

10.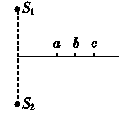如图所示，S₁、S₂是两个振动情况完全相同的机械波波源，振幅为A，a、b、c三点分别位于S₁、S₂连线的中垂线上，且ab＝bc.某时刻a是两列波的波峰相遇点，c是两列波的波谷相遇点，则(　)

A.a处质点的位移始终是2A

B.c处质点的位移始终是－2A

C.b处质点的振幅为2A

D.c处质点的振幅为2A

解析：as₁＝as₂、bs₁＝bs₂、cs₁＝cs₂，故a、b、c三点都为干涉加强点，振幅均为2A，选项C、D正确，选项A、B错误.

答案：CD

非选择题部分3小题，共40分.

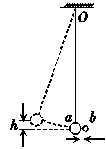
9.如图所示的单摆，摆球a向右摆动到最低点时，恰好与一沿水平方向向左运动的黏性小球b发生碰撞，并粘在一起，且摆动平面不变.已知碰撞前a球摆动的最高点与最低点的高度差为h，摆动的周期为T，a球的质量是b球质量的5倍，碰撞前a球在最低点的速度是b球速度的一半.则碰撞后[2007年高考·北京理综卷](　)

A.摆动的周期为 T

B.摆动的周期为 T

C.摆球最高点与最低点的高度差为0.3h

D.摆球最高点与最低点的高度差为0.25h

解析：单摆的周期与摆球的质量无关，碰后单摆周期不变，选项A、B错误.

碰撞过程中，有：5m₀·－m₀·2＝6m₁v

解得：v＝

故碰后摆球能上摆的最大高度h′＝＝h.故C错误、D正确.

答案：D