5.如图甲所示，滑块A置于光滑的水平面上，一细线的一端固定于倾角θ＝45°、质量为M的光滑楔形滑块A的顶端P处，细线另一端拴一质量为m的小球B.现对滑块施加一水平方向的恒力F，要使小球B能相对斜面静止，恒力F应满足什么条件？

解析：

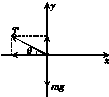
乙

先考虑恒力背离斜面方向(水平向左)的情况.设恒力大小为F1时，B还在斜面上且对斜面的压力为零，此时A、B有共同的加速度a1，B的受力情况如图乙所示，有：

Tsin θ＝mg，Tcos θ＝ma1

解得：a1＝gcot θ

即F1＝(M+m)a1＝(M+m)gcot θ

由此可知，当水平向左的力大于(M+m)gcot θ时，小球B将离开斜面.

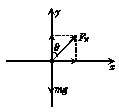对于水平恒力向斜面一侧方向(水平向右)的情况，设恒力大小为F2时，B相对斜面静止时对悬绳的拉力恰好为零，此时A、B的共同加速度为a2，

B的受力情况如图丙所示，有：FNcos θ＝mg，FNsin θ＝ma2

解得：a2＝gtan θ

即F2＝(M+m)a2

＝(M+m)gtan θ

由此可知，当水平向右的力大于(M+m)gtan θ，B将沿斜面上滑

综上可知，当作用在A上的恒力F向左小于(M+m)gcot θ，或向右小于(M+m)gtan θ时，B能静止在斜面上.

答案：向左小于(M+m)gcot θ或向右小于(M+m)gtan θ

4.如图所示，在水平桌面上叠放着质量均为M的A、B两块木板，在木板A的上面放着一个质量为m的物块C，木板和物块均处于静止状态.A、B、C之间以及B与地面之间的动摩擦因数都为μ.若用水平恒力F向右拉动木板A，使之从C、B之间抽出来，已知重力加速度为g，则拉力F的大小应该满足的条件是(已知最大静摩擦力的大小等于滑动摩擦力)(　)

A.F＞μ(2m+M)g　 B.F＞μ(m+2M)g

C.F＞2μ(m+M)g　 D.F＞2μmg

解析：无论F多大，摩擦力都不能使B向右滑动，而滑动摩擦力能使C产生的最大加速度为μg，故＞μg时，即F＞2μ(m+M)g时A可从B、C之间抽出.

答案：C

然后隔离重物利用牛顿第二定律可得：F′－mg＝ma

取立两式可得：F′＝F，故选项C正确.

答案：C

3.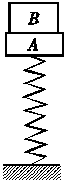如图所示，竖直放置在水平面上的轻弹簧上放着质量为2 kg的物体A，处于静止状态.若将一个质量为3 kg的物体B竖直向下轻放在A上的一瞬间，A对B的压力大小(取g＝10 m/s2)(　)

A.30 N　B.0　C.15 N　D.12 N

解析：刚放上的瞬间，取AB整体为研究对象：

(mA+mB)g－kx0＝(mA+mB)a

其中kx0＝mAg

取B为研究对象：mBg－FN＝mBa

解得：FN＝g＝12 N.

答案：D

12.如图所示，两个用轻线相连的位于光滑水平面上的物块，质量分别为m₁和m₂，拉力F₁和F₂方向相反，与轻线沿同一水平直线，且F₁＞F₂.试求两个物块运动过程中轻线的拉力T.[2004年高考·全国理综卷]

解析：设两物块一起运动的加速度为a，则有：

F₁－F₂＝(m₁+m₂)a

根据牛顿第二定律，对质量为m₁的物块有：

F₁－T＝m₁a

解得：T＝ .

答案：

11.如图所示，物体从光滑斜面上的A点由静止开始下滑，经过B点后进入水平面(设经过B点前后速度大小不变)，最后停在C点.每隔0.2秒通过速度传感器测量物体的瞬时速度，下表给出了部分测量数据.取重力加速度g＝10 m/s²，求：

(1)斜面的倾角α.

(2)物体与水平面之间的动摩擦因数μ.

(3)t＝0.6 s时的瞬时速度v.[2007年高考·上海物理卷]

解析：(1)由前三列数据可知物体在斜面上匀加速下滑时的加速度a₁＝＝5 m/s²，由mgsin α＝ma₁，可得：α＝30°.

(2)由后两列数据可知物体在水平面上匀减速滑行时的加速度大小a₂＝＝2 m/s²，μmg＝ma₂

可得：μ＝0.2.

(3)设0.4 s后再经过t时间物体滑至B点，有：

2+5t＝1.1+2(0.8－t)

解得：t＝0.1 s

即物体在斜面上下滑的时间为0.5 s，则t＝0.6 s时物体在水平面上，设物体在0.6 s时的速度为v，有：

v_1.2＝v－a₂(1.2－0.6)＝1.1 m/s

解得：v＝2.3 m/s.

答案：(1)30°　(2)0.2　(3)2.3 m/s

10.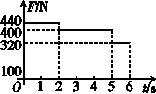一质量m＝40 kg的小孩站在电梯内的体重计上.电梯从t＝0时刻由静止开始上升，在0-6 s内体重计的示数F的变化如图所示.试问：在这段时间内电梯上升的高度是多少？(取g＝10 m/s²)[2006年高考·全国理综卷Ⅱ]

解析：由题图可知，在t＝0到t₁＝2 s的时间内，体重计的示数大于mg，故电梯应做向上的加速运动.设在这段时间内体重计作用于小孩子的力为F₁，电梯及小孩的加速度为a₁，由牛顿第二定律，得：F₁－mg＝ma₁

在这段时间内电梯上升的高度h₁＝a₁t

在t₁＝2 s到t₂＝5 s的时间内，体重计的示数等于mg，故电梯应做匀速上升运动，速度为t₁时刻电梯的速度，即v₁＝a₁·t₁，在这段时间内电梯上升的高度h₂＝v₁(t₂－t₁).

在t₂＝5 s到t₃＝6 s的时间内，体重计的示数小于mg，故电梯应做向上的减速运动.设这段时间内体重计作用于小孩的力为F₂，电梯及小孩的加速度为a₂，由牛顿第二定律，得：mg－F₂＝ma₂

在这段时间内电梯上升的高度

h₃＝v₁(t₃－t₂)－a₂(t₃－t₂)²

电梯上升的总高度h＝h₁+h₂+h₃.

由以上各式，利用牛顿第三定律和题文及题图中的数据，解得：h＝9 m.

答案：9 m

9.如图甲所示，光滑固定细杆与地面成一定倾角，在杆上套有一个光滑小环，小环在沿杆方向的推力F作用下向上运动.推力F与小球速度v随时间变化的规律如图乙所示，g取10 m/s².求：

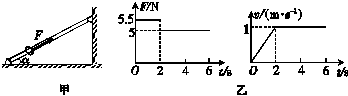
(1)小环的质量m.

(2)细杆与地面间的倾角α.

[2007年高考·上海物理卷]

解析：(1)在0-2 s内有：F₁－mgsin α＝ma

又由v－t图象可知：a＝0.5 m/s²

在2 s以后：F₂＝mgsin α

联立解得：F₁－F₂＝ma

所以m＝＝ kg＝1 kg.

(2)由上式得，sin α＝＝

所以α＝30°.

答案：(1)1 kg　(2)30°

8.在伽利略羊皮纸手稿中发现的斜面实验数据如下表所示，人们推测第二、三列数据可能分别表示时间和长度.伽利略时代的1个长度单位相当于现在的mm，假设1个时间单位相当于现在的0.5 s.由此可以推测实验时光滑斜面的长度至少为　　m，斜面的倾角约为　　度.(取g＝10 m/s²)[2008年高考·上海物理卷]

解析：依题意，第一列数据为时间的平方t²，从数据分析可知第一列数据与第三列数据之比约为1∶32(取平均值后比值为1∶32.75)，即斜面长度与时间的平方成正比，根据当时数据与现在的数据换算关系和匀变速运动公式，可得角度约为(θ≈sin θ＝0.025 rad)1.5°.

答案：2.03　1.5

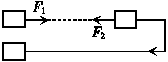
7.在光滑的水平地面上有一静止的物体.现以大小为F₁的水平恒力推这一物体，作用一段时间后换成相反方向的大小为F₂的水平恒力推这一物体；当恒力F₂作用的时间与恒力F₁作用的时间相等时，物体恰好回到原处，此时物体的动能为 32 J，则可知(　)

A.F₂＝2F₁

B.F₂＝3F₁

C.F₁做的功为8 J，F₂做的功为24 J

D.F₁做的功为8 J，F₂做的功为－24 J

解析：

图示为物体的受力情况及运动示意图.

设F₁、F₂的作用时间为t，由题意知：s＝··t²，－s＝(·t)t－··t²

解得：F₂＝3F₁

由W₁＝F₁·s，W₂＝F₂·s，W₁+W₂＝32 J

解得：W₁＝8 J，W₂＝24 J.

答案：BC

6.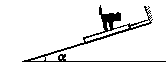如图所示，在倾角为α的固定光滑斜面上，有一用绳子拴着的长木板，木板上站着一只猫.已知木板的质量是猫的质量的2倍.当绳子突然断开时，猫立即沿着板向上跑，以保持其相对斜面的位置不变，则此时木板沿斜面下滑的加速度为[2004年高考·全国理综卷Ⅳ](　)

A.sin α　B.gsin α　C.gsin α　D.2gsin α

解析：本题可用隔离法.猫向上跑时相对于斜面位置不变，即所受合力为零.根据力的平衡原理可知猫所受的沿斜面向上的摩擦力f＝mgsin α，由牛顿第三定律可知木板受猫的沿斜面向下的摩擦力也等于mgsin α.以木板为研究对象，由牛顿第二定律得：

mgsin α+2mgsin α＝2ma，a＝gsin α，故选项C正确.

本题也可用整体法求解.绳子断时，以猫和木板作为一个整体可得沿斜面向下的合力为3mgsin α，而只有木板向下滑动，故：

3mgsin α＝2ma，a＝gsin α.故选项C正确.

答案：C