
2. 已知椭圆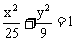 上的点M到该椭圆一个焦点F的距离为2,N是MF的中点,O为椭圆中心,那么线段ON的长是( )
上的点M到该椭圆一个焦点F的距离为2,N是MF的中点,O为椭圆中心,那么线段ON的长是( )
A. 2 B.
4 C.
8 D.
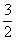
1. 若方程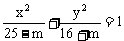 表示焦点在
表示焦点在 轴上的椭圆,则
轴上的椭圆,则 的取值范围为( )
的取值范围为( )
A. (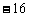 ,25) B. (
,25) B. (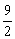 ,25) C.
(
,25) C.
(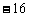 ,
,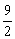 ) D.
(
) D.
(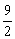 ,
, )
)
(二)椭圆的标准方程及几何性质
1、标准方程是指中心在原点,坐标轴为对称轴的标准位置的椭圆方程。
|
|
中心在原点,焦点在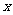 轴上 轴上 |
中心在原点,焦点在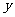 轴上 轴上 |
|
标准方程 |
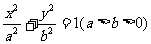 |
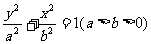 |
|
参数方程 |
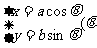 为参数) 为参数) |
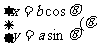 为参数) 为参数) |
|
图 形 |
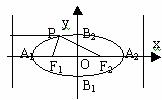 |
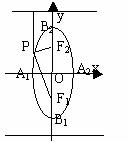 |
|
顶 点 |
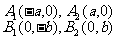 |
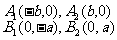 |
|
对称轴 |
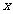 轴, 轴,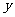 轴;短轴为 轴;短轴为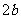 ,长轴为 ,长轴为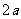 |
|
|
焦 点 |
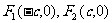 |
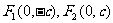 |
|
焦 距 |
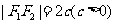 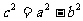 |
|
|
离心率 |
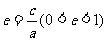 (离心率越大,椭圆越扁) (离心率越大,椭圆越扁) |
|
|
准 线 |
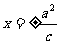 |
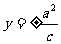 |
|
通 径 |
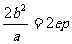 ( (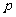 为焦准距) 为焦准距) |
|
|
焦半径 |
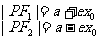 |
 |
|
焦点弦 |
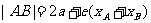 仅与它的中点的横坐标有关 |
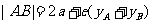 仅与它的中点的纵坐标有关 |
|
焦准距 |
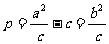 |
说明:方程中的两个参数a与b,确定椭圆的形状和大小,是椭圆的定型条件,焦点F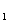 ,F
,F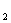 的位置,是椭圆的定位条件,它决定椭圆标准方程的类型,常数a,b,c都大于零,其中a最大且a
的位置,是椭圆的定位条件,它决定椭圆标准方程的类型,常数a,b,c都大于零,其中a最大且a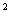 =b
=b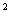 +c
+c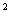
2、椭圆焦点三角形:设P为椭圆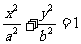 上任意一点,F
上任意一点,F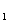 ,F
,F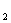 为焦点且∠F
为焦点且∠F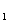 PF
PF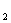 =
=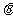 ,则△PF
,则△PF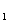 F
F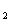 为焦点三角形,S=b
为焦点三角形,S=b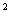 tan
tan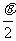 。
。
3、方程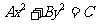 表示椭圆的充要条件是:ABC≠0,且A,B,C同号,A≠B。A>B时,焦点在y轴上,A<B时,焦点在x轴上。
表示椭圆的充要条件是:ABC≠0,且A,B,C同号,A≠B。A>B时,焦点在y轴上,A<B时,焦点在x轴上。
4、弦长公式:x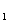 ,x
,x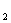 分别为弦PQ的横坐标,弦PQ所在直线方程为y=kx+b,代入椭圆方程整理得Ax2+Bx+C=0,则
分别为弦PQ的横坐标,弦PQ所在直线方程为y=kx+b,代入椭圆方程整理得Ax2+Bx+C=0,则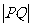 =
=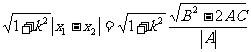 ,若y
,若y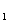 ,y
,y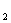 分别为弦PQ的纵坐标,则
分别为弦PQ的纵坐标,则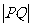 =
= ,
,
5、直线与椭圆的位置关系:设直线l的方程为:Ax+By+C=0,椭圆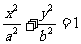 (a﹥b﹥0),组成方程组,消去y(或x)利用判别式△的符号来确定。
(a﹥b﹥0),组成方程组,消去y(或x)利用判别式△的符号来确定。
若△>0 则直线与椭圆有两个交点,
则直线与椭圆有两个交点,
若△=0 则直线与椭圆有一个交点,
则直线与椭圆有一个交点,
若△<0 则直线与椭圆没有交点。
则直线与椭圆没有交点。
6、斜率为k的弦的中点轨迹方程:设弦PQ的端点为P(x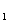 ,y
,y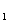 ),Q(x
),Q(x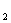 ,y
,y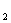 ),中点为M(x
),中点为M(x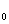 ,y
,y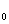 ),把P,Q的坐标代入椭圆方程后作差相减用中点公式和斜率公式可得
),把P,Q的坐标代入椭圆方程后作差相减用中点公式和斜率公式可得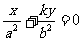 (椭圆内不含端点的线段)
(椭圆内不含端点的线段)
7、设P(x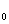 ,y
,y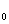 )是椭圆
)是椭圆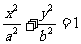 (a﹥b﹥0)上一点,则过P点的切线方程是:
(a﹥b﹥0)上一点,则过P点的切线方程是: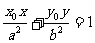
8、点P和椭圆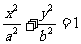 (a﹥b﹥0)的关系:(1)点P(x
(a﹥b﹥0)的关系:(1)点P(x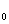 ,y
,y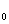 )在椭圆外
)在椭圆外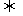
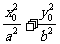 >1,(2)点P(x
>1,(2)点P(x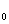 ,y
,y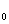 )在椭圆上
)在椭圆上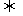
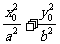 =1,(3)点P(x
=1,(3)点P(x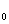 ,y
,y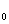 )在椭圆内
)在椭圆内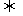
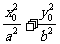 <1
<1
9、椭圆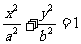 (a﹥b﹥0)按
(a﹥b﹥0)按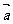 =(x
=(x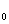 ,y
,y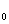 )平移得
)平移得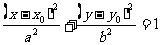 (它的中心、对称轴、焦点、准线方程都按
(它的中心、对称轴、焦点、准线方程都按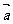 =(x
=(x ,y
,y )作了相应的平移。)
)作了相应的平移。)
[考点指要]
在历年的高考数学试题中,有关圆锥曲线的试题所占的比重约占试卷的15%左右,且题型,数量,难度保持相对稳定:选择题和填空题共2道题,解答题1道,选择题和填空题主要考查圆锥曲线的标准方程,几何性质等;解答题往往是以椭圆,双曲线或抛物线为载体的有一定难度的综合题,问题涉及函数,方程,不等式,三角函数,平面向量等诸多方面的知识,并蕴含着数学结合,等价转化,分类讨论等数学思想方法,对考生的数学学科能力及思维能力的考查要求较高。近几年解答题注意了控制运算量,增加了思维容量,即逻辑思维,数学思维的考查容量有所增加,运算能力的考查略有下降。
主要考查:圆锥曲线的概念和性质;直线与圆锥曲线的位置关系;求曲线的方程;与圆锥曲线有关的定值问题,最值问题,对称问题,范围问题等。曲线的应用问题,探索问题以及圆锥曲线与其它数学内容的交汇问题也将是高考命题的热点。
[典型例题]
例1. 求下列椭圆的标准方程
(1)椭圆的一个顶点为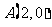 ,其长轴长是短轴长的2倍。
,其长轴长是短轴长的2倍。
分析:题目没有指出焦点的位置,要考虑两种位置.
解:①当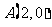 为长轴端点时,
为长轴端点时,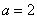 ,
,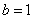 ,椭圆的标准方程为:
,椭圆的标准方程为: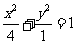 ;
;
②当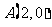 为短轴端点时,
为短轴端点时,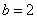 ,
,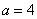 ,椭圆的标准方程为:
,椭圆的标准方程为: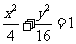 ;
;
说明:椭圆的标准方程有两个,给出一个顶点的坐标和对称轴的位置,是不能确定椭圆的横竖的,因而要考虑两种情况.
选题角度:根据椭圆上的点和长短轴之间的关系求标准方程,考查椭圆的标准方程和思考问题的全面性;
(2)已知中心在原点,焦点在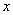 轴上的椭圆与直线
轴上的椭圆与直线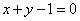 交于
交于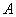 、
、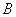 两点,
两点,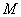 为
为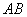 中点,
中点,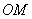 的斜率为0.25,椭圆的短轴长为2。
的斜率为0.25,椭圆的短轴长为2。
解:由题意,设椭圆方程为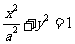
由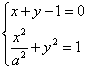 ,得
,得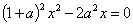 ,
,
∴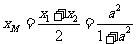 ,
,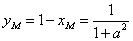 ,
,
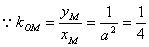 ,∴
,∴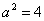 ,
,
∴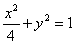 为所求.
为所求.
说明:(1)此题求椭圆方程采用的是待定系数法;(2)直线与曲线的综合问题,经常要借用根与系数的关系,来解决弦长、弦中点、弦斜率问题.
选题角度:根据椭圆的几何特征求椭圆的方程
例2. 已知点P(3,4)是椭圆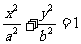 (a﹥b﹥0)上的一点,
两个焦点为F
(a﹥b﹥0)上的一点,
两个焦点为F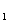 ,F
,F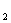 ,若PF
,若PF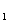 ⊥PF
⊥PF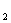 ,试求:
,试求:
(1)椭圆的方程
(2)△PF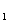 F
F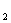 的面积
的面积
解析:(1)解法一:令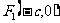 ,
,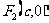 ,则
,则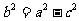 。
。

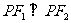 ,
,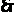
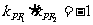 ,
,
即
 ,解得
,解得 ,
,
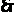 椭圆方程为
椭圆方程为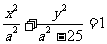 ,
,
 点
点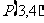 在椭圆上,
在椭圆上,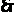
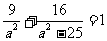 ,
,
解得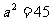 或
或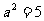
又 ,
,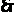
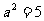 舍去,
舍去,
故所求椭圆方程为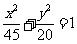 。
。
解法二:
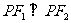 ,
,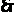
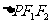 为直角三角形,
为直角三角形,
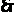
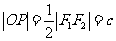
又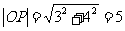 ,
,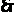
 ,
,
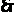 椭圆方程为
椭圆方程为 (以下同解法一)
(以下同解法一)
(2)解法一:
由焦半径公式:
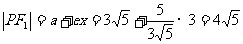 ,
,
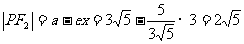 ,
,
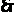
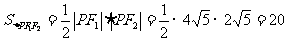 。
。
解法二:P点纵坐标的值即为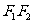 边上的高,
边上的高,
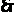
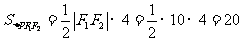 。
。
解法三:由椭圆定义知:
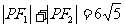 ①
①
又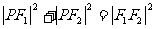 ②
②
①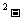 ② 得
② 得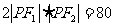 ,
,
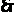
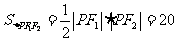
反思:要确定椭圆的标准方程,即确定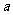 、
、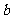 的值,由于
的值,由于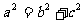 ,故只需求出
,故只需求出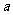 、
、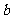 、
、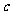 中的任意两个量即可。本例中利用
中的任意两个量即可。本例中利用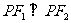 的条件或使用斜率或借助平面几何知识均可求出
的条件或使用斜率或借助平面几何知识均可求出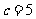 。对于求
。对于求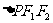 的面积,解法一使用了焦半径公式,解法二利用了第一定义和勾股定理,以上解法都说明在处理解析几何问题时,既可以用代数的方法求值运算,又可以利用某些几何性质。
的面积,解法一使用了焦半径公式,解法二利用了第一定义和勾股定理,以上解法都说明在处理解析几何问题时,既可以用代数的方法求值运算,又可以利用某些几何性质。
例3. 椭圆C: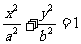 (a﹥b﹥0)的两个焦点为F
(a﹥b﹥0)的两个焦点为F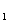 ,F
,F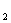 ,点P在椭圆C上,且PF
,点P在椭圆C上,且PF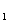 ⊥PF
⊥PF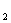 ,︱PF
,︱PF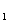 ︱=
︱= ,︱PF
,︱PF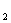 ︱=
︱=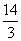
(1)求椭圆C的方程。
(2)若直线l过圆x2+y2+4x-2y=0的圆心M,交椭圆C于A,B两点,且A,B关于点M对称,求直线l的方程.
解析:解法一(1)因为点P在椭圆C上,所以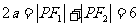 ,
,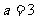 。
。
在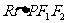 中,
中, ,故椭圆的半焦距
,故椭圆的半焦距 ,从而
,从而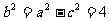 。
。
所以椭圆C的方程为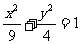 。
。
(2)设A,B的坐标分别为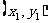 ,
,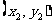 。
。
已知圆的方程为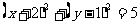 ,所以圆心M的坐标为
,所以圆心M的坐标为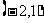 ,从而可设直线
,从而可设直线 的方程为
的方程为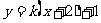 ,代入椭圆C的方程得
,代入椭圆C的方程得
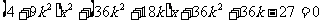 。
。
因为A,B关于点M对称,所以 ,解得
,解得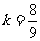 ,所以直线
,所以直线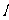 的方程为
的方程为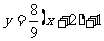 ,即
,即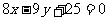 。
。
解法二:(1)同解法一。
(2)已知圆的方程为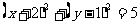 ,所以圆心M的坐标为
,所以圆心M的坐标为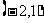 ,设A,B的坐标分别为
,设A,B的坐标分别为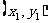 ,
,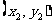 。由题意
。由题意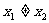 且
且

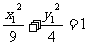 , ①
, ①

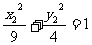 。 ②
。 ②
由①-②得
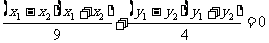 。 ③
。 ③
因为A,B关于点M对称,
所以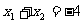 ,
,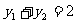 。代入 ③ 得
。代入 ③ 得 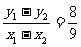 ,
,
即直线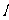 的斜率为
的斜率为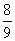 ,所以直线
,所以直线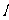 的方程为
的方程为
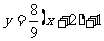 ,
,
即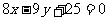 。
。
反思:
(1)利用椭圆的定义求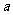 以及已知的条件求
以及已知的条件求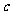 从而求出椭圆方程。
从而求出椭圆方程。
(2)解法一:利用解析几何的基本思想--用代数方法解决几何问题,先求出圆心坐标从而求出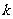 的值。
的值。
解法二:利用点差法求出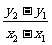 的值,从而求出直线
的值,从而求出直线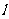 的方程。
的方程。
[模拟试题](答题时间:45分钟)
(一)椭圆的定义
1、第一定义:平面内与两个定点为F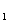 ,F
,F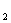 的距离的和等于常数(大于
的距离的和等于常数(大于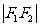 )的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。特别地,当常数等于
)的点的轨迹叫做椭圆,这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。特别地,当常数等于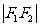 时,轨迹是线段F
时,轨迹是线段F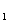 F
F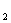 ,当常数小于
,当常数小于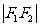 时,无轨迹。
时,无轨迹。
2、第二定义:平面内到定点F的距离和到定直线l的距离之比等于常数e(0﹤e﹤1)的点的轨迹,叫做椭圆,定点F叫椭圆的焦点,定直线l叫做椭圆的准线。e叫椭圆的离心率。
椭圆有两个焦点,两条准线。该定义中的焦点和准线具有“对应性”,即左焦点对应左准线,右焦点对应右准线。
掌握椭圆的定义,标准方程,能根据条件利用待定系数法求椭圆的方程,掌握椭圆的几何性质。了解椭圆的参数方程,能根据方程讨论曲线的性质,了解椭圆的一些实际应用,掌握直线与椭圆的位置关系的判断方法,能够正确熟练地解决直线和椭圆的位置关系的一些问题。
椭圆的定义、标准方程及几何性质
⒈分子结构鉴定的常用方法:
⑴化学方法:设计实验,利用特征反应鉴定出官能团,再制备它的衍生物进一步确认。
⑵物理方法:质谱、 、紫外光谱、 等。
⒉红外光谱:
原理: 在红外光谱图上的位置不同→含有 。
⒊核磁共振氢谱:
原理:不同化学环境中的 原子的核磁共振氢谱图上的位置不同,且吸收峰的面积(高度)与 原子数成正比→有机物中有几种不同类型的 原子及 原子数目。
试题枚举
[例1]某气态烃1L(标态)跟适量O2用电火花点燃,二者确好完全反应,生成物在1atm、
273℃时体积为xL ,冷却到标态时体积为yL,则该烃的分子式为 。
解析:本题用比例法求解。根据阿伏加德罗定律可知:同温、同压时气体的体积之比等于物质的量之比,气态烃1L(标态)与CO2 yL(标态)的条件相同,具有可比性得出该烃中含有y个C原子;而xL为H2O、CO2在1atm、273℃时体积,与烃的体积1L条件不同,要将体积转化为同一条件才可比较,可统一转化为1atm、273℃,此时气态烃的体积为2L,水的体积为x-2y,由此推出烃分子中H个数为x-2y。
答案:CyHx-2y
[例2] 下列是烃的衍生物中四个常见分子(溴乙烷、乙醇、乙醛、乙酸)的比例模型,其中表示乙醛分子的是( )

解析:根据题给条件, 4种分子中均只有2个C原子,且均含有有-CH3,从图中可看出左边为-CH3,与-CH3相连的黑色原子为C原子,与该C原子相连的白色原子为H,黑色原子为O或Br,根据各原子的成键数目及特点,可推出四种物质:
A为乙酸,B为乙醇,C为溴乙烷,D为乙醛。
答案:D
[例3]烃A的蒸汽对N2 的相对密度为5.07,若A为链烃,其分子式为 其同分异构体中支链最多的一种异构体的名称是 若A为环烃,其分子式为 。
解析:商余法解题的步骤是:Mr÷12=x……y ,分子式为CxH y,在此基础上,可用
C~12H、CH4 ~O、2CH4 ~2O的式量相等进行替代,可得到多个符合题意的分子式。
但替代后所得分子式中H原子数不得超过C原子数的2n+2个。
本题中Mr(A)=5.07×28=142 , 142÷12=10……22 C10H22 ,用1个C替换12个
H可得另一符合题意的分子式:C11H10
答案:C10H22 2,2,3,3,4-三甲基戊烷或 2,2,3,4,4-三甲基戊烷 ,C11H10 。
[例4]两种气态烃以任意比例混合,在105 ℃时1 L该混合烃与9 L氧气混合,充分燃烧
后恢复到原状态,所得气体体积仍是10 L。下列各组混合烃中不符合条件的是
A.CH4、C2H4 B.CH4、C3H6
C.C2H4、C3H4 D.C2H2、C3H6
解析:由题意T>100 ℃(水为气体)。而此状况下燃烧前后体积不变,则烃分子含氢原子数等于4。所以选B项;又两烃是以任意比例混合,则D项也应选。故此题选B、D。
答案:BD
[例5]质子核磁共振谱(PMR)是研究有机物结构的有力手段之一,在所研究的化合物分子
中,每一结构中的等性氢原子在PMR谱中都给出了相应的峰(信号)。峰的强度与结
构中的H原子数成正比,例如乙酸分子的PMR谱中有两个信号峰,其强度比为3:1。现有某化学式为C3H6O2的有机物的PMR谱有三个峰,其强度比为3:2:1,则该有机物的结构简式不可能是( )
A.CH3CH2COOH B.CH3COOCH3
C.HCOOCH2CH3 D.CH3COCH2OH
简析:在PMR谱中,等性氢原子都给出了相应的峰(信号),峰的强度与结构中的H原
子数成正比。因此PMR谱有三个峰说明有三种化学环境不同的氢原子,而且其个数比为3:2:1。
答案:B
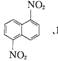 [例6]在一定条件下,萘可以被硝酸和硫酸的混合酸硝化生成二硝基物,它是1,5-二
[例6]在一定条件下,萘可以被硝酸和硫酸的混合酸硝化生成二硝基物,它是1,5-二
硝基萘 、1,8-二硝基萘 的混合物,后者可溶于质量分数大于
98%的硫酸,而前者不能。利用这一性质可将这两种异构体分离。将上述硝化产物加入适量98%的硫酸,充分搅拌,用耐酸漏斗过滤,欲从滤液中得到固体1,8-二硝基萘,应采用的方法是( )
A.蒸发浓缩结晶 B.向滤液中加水过滤
C.用碳酸钠溶液处理滤液 D.将滤液缓缓加入水中
简析:本题的关键是读懂题意,加入98%的硫酸后,1,5-二硝基萘不溶解,而1,8-二硝基萘溶于硫酸,这样得到了固体与液体的混合物,要用过滤的方法分离;分离后再将硫酸稀释,1,8-二硝基萘也析出,但只能将滤液缓缓加入水中,否则导致事故的发生。另外,不能将滤液用碳酸钠溶液处理,因该操作危险又浪费试剂。
答案:D
⒈最简式法:先由各元素的质量分数求出最简式 ,再由Mr求出分子式。(元素种类较少)
n(C)∶n(H)∶n(O)=ω(C)/12∶ω(H)/1∶ω(O)/16
⒉设n法:由元素X的ω(X)=n(X)·Ar(X)/Mr,得出分子中X的原子个数为:
n(X)=ω(X)·Mr/Ar(X)
⒊商余法:Mr÷12=x……y ,分子式为CxH y,然后用替换法写出可能的分子式
C-12H、O-CH4 如:Mr=58,58÷12=4…10,C4H 10,C3H6O,C2H2O2
⒋比例法:已知燃烧、反应前后的质量、物质的量、体积的定量关系
⒌通式法:根据题意先设有机物的分子式,再由题中条件立方程式(组)解答
⒍平均分子式法:C2.5H4
⒎其它方法:根据分子结构图、球棍模型或比例模型确定
⒈元素分析的目的是 ,
常用分析方法是
思考:如何进行元素C、H、O、N、X的测定?
⒉相对分子质量的测定
测定方法 ,该法是现代最快速、微量、精确测定相对分子质量的方法,该法测
出的 的数值即为未知物的相对分子质量
简介:其它测定M的方法:标态密度法、相对密度法、设n法
思考:⑴分离与提纯的区别;⑵除杂三原则: 、 、 。
⒈蒸馏
⑴蒸馏法适用于 的有机混合物的分离。
⑵必须的玻璃仪器和用品
温度计水银球位于 ;加热前加素烧瓷片,目的是 。
⒉重结晶:
重结晶适用于 的有机混合物的分离与提纯。
对溶解度的要求:杂质 ,被提纯的有机物 。
操作步骤: → →
所需玻璃仪器有 。
⒊萃取:
萃取适用于 ;
萃取剂的要求 ;
仪器: ;
操作:振荡,静置分层,打开 口活塞,下层液体从 口放出,上层液体从 口倒出。
其它分离、提纯的方法还有(至少写3种) 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com