
5.若F1、F2为双曲线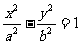 的左、右焦点,O为坐标原点,
的左、右焦点,O为坐标原点,
P在双曲线左支上,M在右准线上,且满足
(1)求此双曲线的离心率;
(2)若此双曲线过点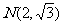 ,求双曲线方程;
,求双曲线方程;
(3)设(2)中双曲线的虚轴端点为B1,B2(B1在y轴正半轴上),求B2作直线AB与双曲线交于A、B两点,求 时,直线AB的方程.
时,直线AB的方程.
解:(1)由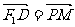 知四边形PF1OM为平行四边形,又由
知四边形PF1OM为平行四边形,又由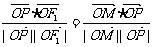
知 为菱形,设半焦距为c,由
为菱形,设半焦距为c,由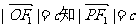 ,
,
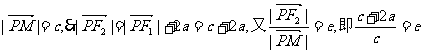
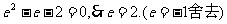
(2)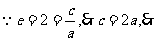 双曲线方程为
双曲线方程为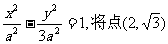 代入,
代入,
有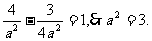 即所求双曲线方程为
即所求双曲线方程为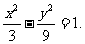
(3)依题意得B1(0,3),B2(0,-3).设直线AB的方程为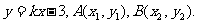
则由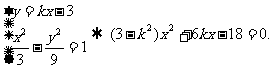
∵双曲线的渐近线为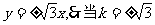 时,AB与双曲线只有一个交点,
时,AB与双曲线只有一个交点,
即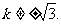
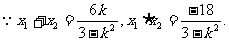
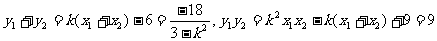
又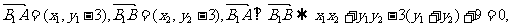
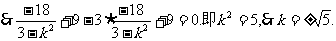
故所求直线AB的方程为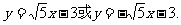
函数与导数:
4. 已知两点 、
、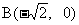 , 动点P在y轴上的射影为 Q,
, 动点P在y轴上的射影为 Q,
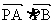
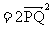 .
.
(1) 求动点P的轨迹E的方程;
(2) 设直线#过点A, 斜率为k. 当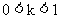 时, 曲线E的上支上有且仅有一点C到直线l的距离为
时, 曲线E的上支上有且仅有一点C到直线l的距离为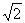 , 试求k的值及此时点C的坐标.
, 试求k的值及此时点C的坐标.
(1)设动点P的坐标为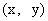 , 则点Q的坐标为
, 则点Q的坐标为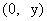 ,
,
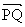
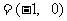 ,
, 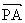
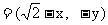 ,
,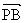
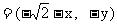 ,
,
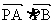 =
=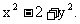 ……(3分) 由题意得
……(3分) 由题意得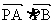
 , 得
, 得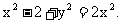
∴所求动点P的轨迹方程为: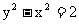
(2)设直线l: 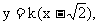
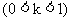
由题意点C在与直线l平行, 且与l之间的距离为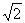 的直线上.
的直线上.
设直线l’: 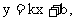 则得
则得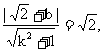 即
即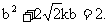 ……①
……①
把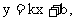 代入
代入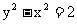 , 且整理得
, 且整理得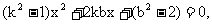
则由题意知: △= 即
即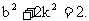 ……②
……②
由①-②得: 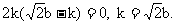
由方程组: 
此时, 由方程组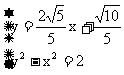 , 得点C的坐标为
, 得点C的坐标为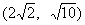
3.已知常数a > 0,向量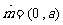 ,
, ,经过定点A (0,–
a )以
,经过定点A (0,–
a )以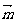 +
+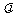
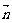 为方向向量的直线与经过定点B (0,a)以
为方向向量的直线与经过定点B (0,a)以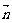 + 2
+ 2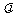
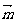 为方向向量的直线相交于点P,其中
为方向向量的直线相交于点P,其中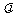 ∈R.
∈R.
(Ⅰ)求点P的轨迹C的方程;
(Ⅱ)若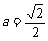 ,过E (0,1)的直线l交曲线C于M、N两点,求
,过E (0,1)的直线l交曲线C于M、N两点,求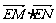 的取值范围.
的取值范围.
解:(Ⅰ)设P点的坐标为(x,y),则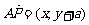 ,
,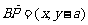 ,
,
又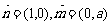 ,故
,故 ,
,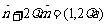 .
.
由题知向量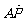 与向量
与向量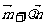 平行,故
平行,故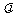 (y + a) = ax.
(y + a) = ax.
又向量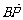 与向量
与向量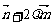 平行,故y – a = 2
平行,故y – a = 2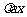 .
.
两方程联立消去参数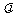 ,得点P (x,y)的轨迹方程是
,得点P (x,y)的轨迹方程是
(y + a)(y – a) = 2a2x2,即y2 – a2 = 2a2x2.
(Ⅱ)∵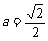 ,故点P的轨迹方程为2y2 – 2x2
= 1,
,故点P的轨迹方程为2y2 – 2x2
= 1,
此时点E (0,1)为双曲线的焦点.
①若直线l的斜率不存在,其方程为x = 0,l与双曲线交于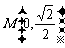 、
、
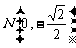 ,此时
,此时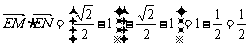 .
.
②若直线l的斜率存在,设其方程为y = kx + 1,代入2y2 – 2x2 = 1化简得
2(k2 – 1) x2 + 4kx + 1 = 0.
∴直线l与双曲线交于两点,
∴△= (4k)2 – 8 (k2 – 1) > 0且k2 – 1≠0.解得k≠±1.
设两交点为M (x1,y1)、N (x2,y2),
则x1 + x2 =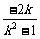 ,x1x2 =
,x1x2 =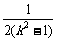 .
.
此时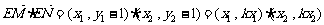
= x1x2
+ k2x1x2 = (k2
+ 1) x1x2 =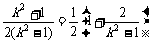 .
.
当– 1 < k < 1时,k2 – 1 < 0,故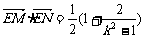 ≤
≤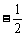 ;
;
当k > 1或k < – 1时,k2 – 1 > 0,故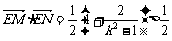 .
.
综上所述,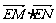 的取值范围是
的取值范围是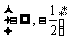 ∪
∪ .
.
2.已知O为坐标原点,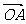 =(2,1),
=(2,1),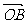 =(1,7),
=(1,7),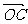 =(5,1),
=(5,1),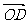 =x
=x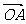 ,y=
,y= ·
·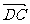 (x,y∈R)
(x,y∈R)
(Ⅰ)求点P(x,y)的轨迹方程;
(Ⅱ)将点P(x,y)的轨迹按向量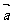 =(-2,8)平移到曲线C,M、N是曲线C上的两不同的点,如果
=(-2,8)平移到曲线C,M、N是曲线C上的两不同的点,如果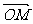 ⊥
⊥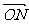 ,求证直线MN恒过一定点,并求出定点坐标.
,求证直线MN恒过一定点,并求出定点坐标.
解:(Ⅰ)∵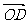 =x
=x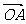 =x(2,1)=(2x,x) ∴D(2x,x)
=x(2,1)=(2x,x) ∴D(2x,x)
∵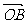 =(1,7),
=(1,7),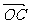 =(5,1) ∴B(1,7),C(5,1)
=(5,1) ∴B(1,7),C(5,1)
∴ =(1-2x,7-x),
=(1-2x,7-x),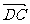 =(5-2x,1-x)
=(5-2x,1-x)
∴y= ·
·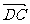 =(1-2x)·(5-2x)+(7-x)(1-x)=5x2-20x+12
=(1-2x)·(5-2x)+(7-x)(1-x)=5x2-20x+12
∴y=5(x-2)2-8这就是所求的点P(x,y)的轨迹方程
(Ⅱ)将y=f(x)的图象按向量平移到曲线C,所得的曲线C的方程为:y=5x2
设M(x1,y1),N(x2,y2)则OM⊥ON
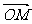 ·
·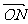 =
= x1x2+y1y2=0
x1x2+y1y2=0
设直线MN的方程为:y=kx+y0(k≠0)代入y2=5x得
k2x2+(2ky0-5)x+y02=0
Δ=(2ky0-5)-4k2y02=25-20ky0>0即ky0<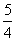 且x1+x2=
且x1+x2=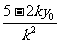 ,x1x2=
,x1x2=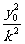
∴y1y2=(kx1+y0)(kx2+y0)=k2x1x2+ky0(x1+x2)+y02=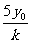 于是
于是
y02=-5(ky0)∴k=-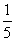 y0(显然y0≠0且满足ky0<
y0(显然y0≠0且满足ky0<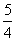 )
)
故直线MN的方程为:
∴y=-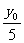 (x-5)
(x-5)
所以直线MN恒过定点(5,0)
1.过椭圆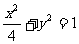 的右焦点F作直线l交椭圆于M、N两点,设
的右焦点F作直线l交椭圆于M、N两点,设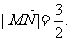
(Ⅰ)求直线l的斜率k;
(Ⅱ)设M、N在椭圆右准线上的射影分别为M1、N1,求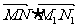 的值.
的值.
解:(Ⅰ)F(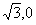 ) l:
) l:
由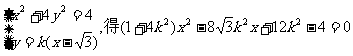
设M ①
①
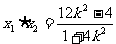 ②
②
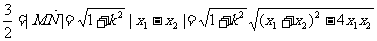 ③
③
把①②代入③,并整理,得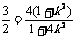
解得 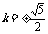
(Ⅱ)设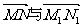 的夹角为
的夹角为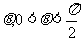
则由(Ⅰ)知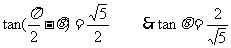 ∴
∴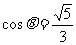
∴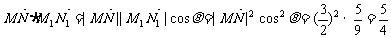
5.投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分,经过
多次试验,某生投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋。
(Ⅰ)求该人在4次投掷中恰有三次投入红袋的概率。
(Ⅱ)[文]求该人两次投掷后得2分的概率。
[理]求该人两次投掷后得分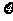 的数学期望。
的数学期望。
解:(Ⅰ)、“飞碟投入红袋”,“飞碟投入蓝袋”,“飞碟不入袋”分别记
为事件A,B,C。则由题意知: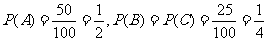
因每次投掷飞碟为相互独立事件,故4次投掷中恰有三次投入红袋的概率为;
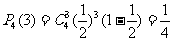
(Ⅱ)、两次投掷得分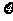 的得分可取值为0,1,2,3,4则:
的得分可取值为0,1,2,3,4则: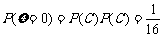
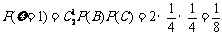
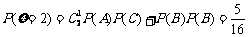
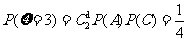 ;
;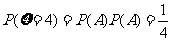
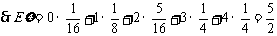
解析几何
4.在一次由三人参加的围棋对抗赛中,甲胜乙的概率为0.4,乙胜丙的概率为0.5,丙胜甲的概率为0.6,比赛按以下规则进行;第一局:甲对乙;第二局:第一局胜者对丙;第三局:第二局胜者对第一局败者;第四局:第三局胜者对第二局败者,求:
(1)乙连胜四局的概率;
(2)丙连胜三局的概率.
解:(1)当乙连胜四局时,对阵情况如下:
第一局:甲对乙,乙胜;第二局:乙对丙,乙胜;第三局:乙对甲,乙胜;第四局:乙对丙,乙胜.
所求概率为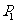 =
=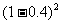 ×
×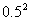 =
=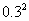 =0.09
=0.09
∴ 乙连胜四局的概率为0.09.
(2)丙连胜三局的对阵情况如下:
第一局:甲对乙,甲胜,或乙胜.
当甲胜时,第二局:甲对丙,丙胜.第三局:丙对乙,丙胜;第四局:丙对甲,丙胜.
当乙胜时,第二局:乙对丙,丙胜;第三局:丙对甲,丙胜;第四局:丙对乙,丙胜.
故丙三连胜的概率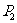 =0.4×
=0.4×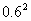 ×0.5+(1-0.4)×
×0.5+(1-0.4)×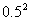 ×0.6=0.162.
×0.6=0.162.
3.从原点出发的某质点M,按向量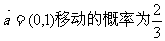 ,按向量
,按向量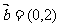 移动的概率为
移动的概率为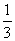 ,设M可到达点(0,n)的概率为Pn.
,设M可到达点(0,n)的概率为Pn.
(1)求P1和P2的值;
(2)求证: ;
;
(3)求Pn的表达式.
解:(1)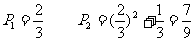
(2)M到达(0,n+2)有两种情况
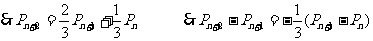
(3)数列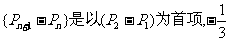 为公比的等比数列
为公比的等比数列
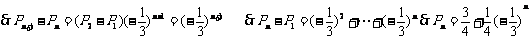
2.
某篮球职业联赛总决赛在甲、乙两支球队之间进行,比赛采用五局三胜制,即哪个队先胜三场即可获得总冠军。已知在每一场比赛中,甲队获胜的概率均为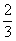 ,乙队获胜的概率均为
,乙队获胜的概率均为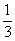 。求:
。求:
(I)甲队以3:0获胜的概率;
(II)甲队获得总冠军的概率。
解:(I)设“甲队以3:0获胜”为事件A,则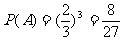
(II)设“甲队获得总冠军”为事件B,
则事件B包括以下结果:3:0;3:1;3:2三种情况
若以3:0胜,则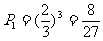 ;
;
若以3:1胜,则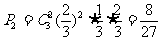
若以3:2胜,则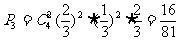
所以,甲队获得总冠军的概率为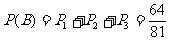
1.甲与乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次为ξ;乙用这次枚硬币掷2次,记正面朝上的次为η.
(Ⅰ)分别求ξ和η的期望;
(Ⅱ)规定;若ξ>η,则甲获胜,若ξ<η,则乙获胜,分别求出甲和乙获胜的概率.
解:(Ⅰ)依题意ζ~B(3,0.5),η~B(2,0.5),所以
Eζ=3×0.5=1.5, Eη=2×0.5=1
(Ⅱ)P(ζ=0)=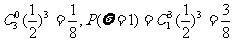
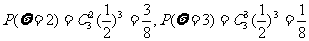

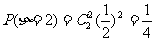
甲获胜有以下情形:ζ=1,η=0,ζ=2,η=0,1;ζ=3,η=0,1,2
则甲获胜的概率为 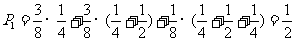
乙获胜有以下情形:η=1,ζ=0,η=2,ζ=0,1
则乙获胜的概率为 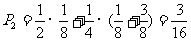
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com