
4.子弹以900m/s的速度从枪筒射出,汽车在北京长安街上行使,时快时慢,
20min行使了18km,汽车行驶的速度是54km/h,则 ( )
A、900m/s是平均速度 B、900m/s是瞬时速度
C、54km/h是平均速度 D、54km/s瞬时速度
3.下列关于路程和位移的说法中,正确的是 ( )
A.位移就是路程.
B.位移的大小永远不等于路程.
C.若物体作单向的直线运动,位移的大小就等于路程.
D.位移描述直线运动,是矢量;路程描述曲线运动,是标量.
2.关于时间和时刻,下列说法正确的是 ( )
A.物体在第5 s末时,指的是时刻
B.物体在5 s内指的是物体在4 s末到5 s末这l s的时间
C.物体在第5 s内指的是物体在4 s末到5 s末这l s的时间
D.第4 s末就是第5 s初.指的是同一时刻
1.关于质点的下列说法中,正确的是( )
A.质量很小的物体都可看作质点.
B.体积很小的物体都可看作质点.
C.在任何情况下,地球都不可以看作质点.
D.一个物体可否视为质点,要看研究问题的具体情况而定.
4.由原点O向三次曲线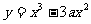 引切线,切于点P1(x1,y1)(O,P1两点不重合),再由P1引此曲线的切线,切于点P2(x2,y2)(P1,P2不重合).如此继续下去,得到点列
引切线,切于点P1(x1,y1)(O,P1两点不重合),再由P1引此曲线的切线,切于点P2(x2,y2)(P1,P2不重合).如此继续下去,得到点列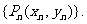
(1)求x1;
(2)求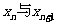 满足的关系式;
满足的关系式;
(3)若a>0,试判断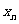 与a的大小关系并说明理由.
与a的大小关系并说明理由.
(1)解:由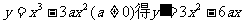
过曲线上点P1(x1,y1)的切线L1的斜率为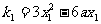
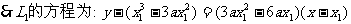
又
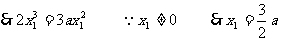
(2)过曲线上的点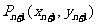 的切线方程是:
的切线方程是:
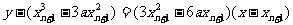
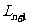 过曲线上点
过曲线上点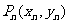
故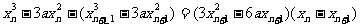
即: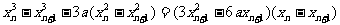
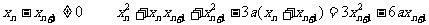
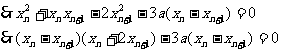
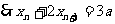
(3)由(2)得: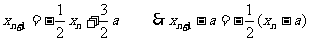
故数列 为首项,公比为
为首项,公比为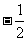 的等比数列.
的等比数列.
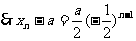
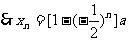
∵ ∴当n为偶数时:
∴当n为偶数时: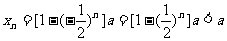
当n为奇数时: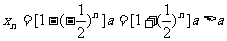
3.已知函数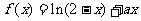 在开区间(0,1)内是增函数
在开区间(0,1)内是增函数
(1)求实数a的取值范围
(2)若数列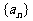 满足
满足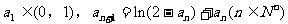 ,证明
,证明
(3)若数列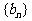 满足
满足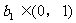 ,
,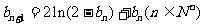 ,问数列
,问数列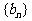 是否单调?
是否单调?
解:(1)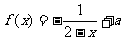 ,由于
,由于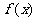 在(0,1)内是增函数
在(0,1)内是增函数
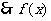 >0,即
>0,即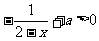 在
在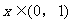 时恒成立
时恒成立
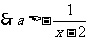 恒成立,而
恒成立,而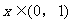 时,
时,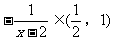
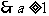 即为所求
即为所求
(2)由题意知当n=1时,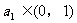 ,假设当
,假设当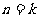 时,有
时,有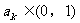
则当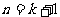 时有
时有 且
且
(由(1)知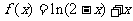 在(0,1)上是增函数)
在(0,1)上是增函数)
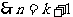 时命题成立,故
时命题成立,故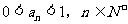
又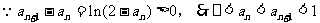
(3)数列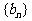 不具有单调性
不具有单调性
令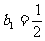 ,则
,则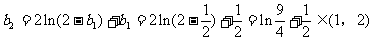
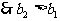 ,又
,又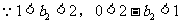
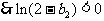
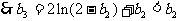 ,由此表明数列
,由此表明数列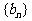 没有单调性
没有单调性
2.设平面上的动向量a=(s,t),b=(-1,t2-k)其中s,t为不同时为0的两个实数,实
数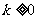 ,满足a⊥b,
,满足a⊥b,
(1)求函数关系式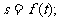
(2)若函数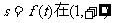 上是单调增函数,求证:
上是单调增函数,求证: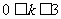 ;
;
(3)对上述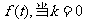 ,存在正项数列
,存在正项数列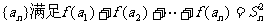 ,其中
,其中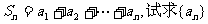 通项公式并证明
通项公式并证明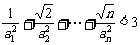 .
.
(1)解: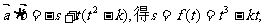
(2)证明: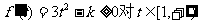 成立,
成立,
故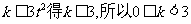 ;
;
(3)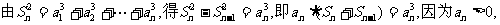
故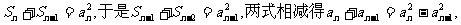
因为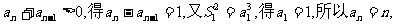
事实上,
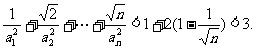
方法1: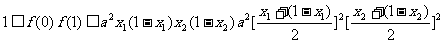
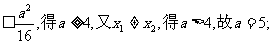
方法2:
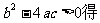

1.把正奇数数列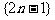 中的数按上小下大、左小右大的原则排成如下三角形数表:
中的数按上小下大、左小右大的原则排成如下三角形数表:
1
3 5
7 9 11
- - - -
- - - - -
设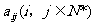 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第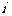 行、从左往右数第
行、从左往右数第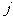 个数。
个数。
(I)若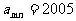 ,求
,求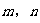 的值;
的值;
(II)已知函数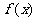 的反函数为
的反函数为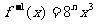
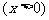 ,若记三角形数表中从上往下数第n行各数的和为
,若记三角形数表中从上往下数第n行各数的和为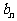 ,求数列
,求数列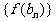 的前n项和
的前n项和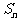 。
。
解:(I) 三角形数表中前
三角形数表中前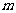 行共有
行共有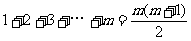 个数,
个数,
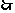 第
第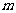 行最后一个数应当是所给奇数列中的第
行最后一个数应当是所给奇数列中的第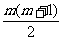 项。
项。
故第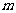 行最后一个数是
行最后一个数是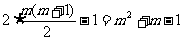
因此,使得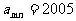 的m是不等式
的m是不等式 的最小正整数解。
的最小正整数解。
由 得
得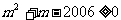
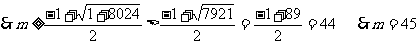
于是,第45行第一个数是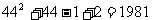
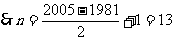
(II) ,
,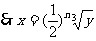 。
。
故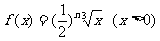
 第n行最后一个数是
第n行最后一个数是 ,且有n个数,若将
,且有n个数,若将 看成第n行第一个数,则第n行各数成公差为-2的等差数列,故
看成第n行第一个数,则第n行各数成公差为-2的等差数列,故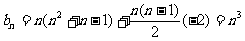 。
。
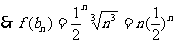
故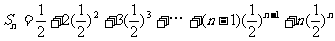
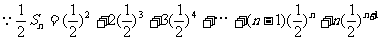 ,
,
两式相减得:
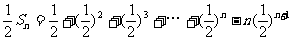
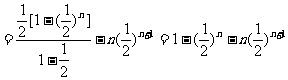
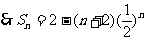
2.设函数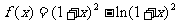
(1)求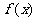 的单调区间;
的单调区间;
(2)若关于x的方程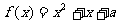 在
在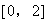 上恰有两个不同的实数根,求实数a的取值范围。
上恰有两个不同的实数根,求实数a的取值范围。
解:(1) 的定义域为(
的定义域为( ,
,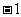 )
)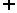 (1,
(1, )
)
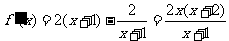
由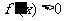 得
得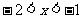 或
或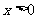
由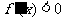 得
得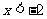 或
或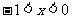
所以 在(
在(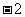 ,
,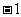 )和(0,
)和(0, )内为增函数,在(
)内为增函数,在( ,
,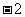 )和(
)和(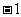 ,0)内为减函数
,0)内为减函数
(2)方程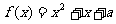 即
即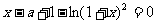
令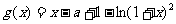
则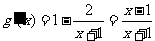
由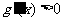 得
得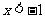 或
或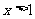
由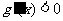 得
得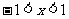
∴ 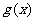 在
在 递减,在
递减,在 递增
递增
所以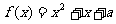 ,即
,即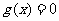 在
在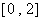 上恰有两个不同的实根是
上恰有两个不同的实根是

解得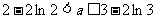
数列综合:
1.函数 的图象上有两点A(0,1)和B(1,0)
的图象上有两点A(0,1)和B(1,0)
(Ⅰ)在区间(0,1)内,求实数a使得函数 的图象在x=a处的切线平行于直线AB;
的图象在x=a处的切线平行于直线AB;
(Ⅱ)设m>0,记M(m,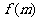 ),求证在区间(0,m)内至少有一实数b,使得函数图象在x=b处的切线平行于直线AM.
),求证在区间(0,m)内至少有一实数b,使得函数图象在x=b处的切线平行于直线AM.
(Ⅰ)解:直线AB斜率kAB=-1 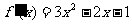
令
解得 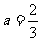
(Ⅱ)证明:直线AM斜率 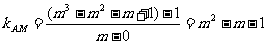
考察关于b的方程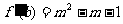
即3b2-2b-m2+m=0
在区间(0,m)内的根的情况
令g(b)= 3b2-2b-m2+m,则此二次函数图象的对称轴为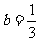
而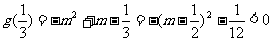
g(0)=-m2+m=m(1-m)
g(m)=2m2-m-m(2m-1)
∴(1)当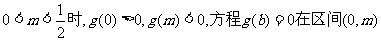 内有一实根
内有一实根
(2)当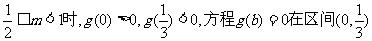 内有一实根
内有一实根
(3)当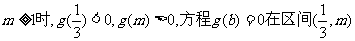 内有一实根
内有一实根
综上,方程g(b)=0在区间(0,m)内至少有一实根,故在区间(0,m)内至少有一实数b,使得函数图象在x=b处的切线平行于直线AM
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com