1.关于闭合电路的性质，下列说法正确的是(　)

A.外电路断路时，路端电压最高

B.外电路短路时，电源的功率最大

C.外电路的电阻变大时，电源的输出功率变大

D.不管外电路的电阻怎样变化，其电源的内外电压之和保持不变

解析：由闭合电路欧姆定律可知，E＝Ir+U_外，当外电路断路时，即I＝0，此时U_外＝E，路端电压最大；外电路短路时，电路中的电流最大，此时，电源的功率也最大；电源的输出功率P＝I²R＝R＝，只有当R＝r时，电源的输出功率才最大.

答案：ABD

6.北京正负电子对撞机的储存环是周长为240 m的近似圆形轨道.当环中电子以光速的的速度流动而形成的电流是10 mA时，环中运行的电子数目为(已知光速c＝3×10⁸ m/s，电子的电荷量e＝1.6×10^－19 C)(　)

A.5×10¹⁰　B.5×10¹¹　C.1×10²　D.1×10⁴

解析：设单位长度上的电子数目为n，则单位长度上的电子所带的电荷量q′＝ne

t秒内电子通过的距离s＝×ct

t秒内通过某截面的电荷量q＝sq′＝

由I＝得：I＝

所以n＝

环中运行的电子数目N＝240n

＝240×

＝5×10¹¹.

答案：B

第50讲　闭合电路的欧姆定律

体验成功

5.一个电解槽的额定电压为U，电流为I，两极间电解液的电阻为R.当它正常工作时，下列说法正确的是(　)

A.电解槽的功率为

B.电解槽的热功率为I²R

C.电解槽的输出功率为UI－I²R

D.电解槽的热功率为

解析：电解槽的功率指的是这一装置消耗电能的总功率P＝UI

电解槽的热功率由焦耳定律有：P_热＝I²R

电解槽的输出功率指的是这一装置把电能转化为化学能的功率(电解出单质)，故P_输＝UI－I²R.

答案：BC

4.在神经系统中，神经纤维分为有髓鞘和无髓鞘两大类.现代生物学认为，髓鞘是由多层类脂物质--髓质累积而成的，具有很大的电阻，经实验测得髓质的电阻率ρ＝8×10⁶ Ω·m.某生物体中某段髓质神经纤维可看做高20 cm、半径为4 cm的圆柱体，当在其两端加上电压U＝100 V时，该神经发生反应，则引起神经纤维产生感觉的最小电流为(　)

A.0.31 μA　 B.0.62 μA

C.0.15 μA　 D.0.43 μA

解析：根据电阻定律，可得神经纤维的电阻为：

R＝ρ＝8×10⁶× Ω＝3.18×10⁸ Ω

根据部分电路的欧姆定律可知：

I＝＝0.31×10^－6 A＝0.31 μA.

答案：A

3.如图所示，两个截面不同、长度相等的均匀铜棒串接在电路中，两端的电压为U，则(　)

A.通过两棒的电流不相等

B.两棒的自由电子定向移动的平均速率不同

C.两棒内的电场强度不同，细棒内场强E₁大于粗棒内场强E₂

D.细棒的电压U₁大于粗棒的电压U₂

解析：由R＝ρ可知，R₁＞R₂

又由串联电路的特点知：I₁＝I₂＝I

故U₁＝IR₁＞U₂＝IR₂

E₁＝＞E₂＝

可知选项A错误，C、D正确.

又因为铜棒内的电流是自由电子定向移动形成的，即I＝neSv，由S₁＜S₂可解得v₁＞v₂，选项B正确.

答案：BCD

2.一根粗细均匀的镍铬丝的横截面的直径为d，电阻是R，把它拉制成直径是的均匀细丝后，它的电阻变成(　)

A.R　　　B.10000R

C.R　 D.100R

解析：R＝ρ

拉长后L′＝＝100L

故R′＝ρ＝10000R.

答案：B

1.用一个内阻不计的电源和三根电热丝加热一壶水，已知电热丝的电阻R₁＝R₂＞R₃，则加热最快的方法是(　)

A.三根电热丝并联

B.三根电热丝串联

C.R₁、R₃并联再与R₃串联

D.R₂、R₃并联再与R₃串联

解析：三根电热丝并联时，三根电热丝的电功率之和最大，大小为：P_总＝U²(++).

答案：A

11.有两个完全相同的小滑块A和B，A沿光滑水平面以速度v₀与静止在平面边缘O点的B发生正碰，碰撞中无机械能损失.碰后B运动的轨迹为OD曲线，如图所示.

(1)已知滑块质量为m，碰撞时间为Δt，求碰撞过程中A对B平均冲力的大小.

(2)为了研究物体从光滑抛物线轨道顶端无初速下滑的运动，特制做一个与B平抛轨道完全相同的光滑轨道，并将该轨道固定在与OD曲线重合的位置，让A沿该轨道无初速下滑(经分析，A下滑过程中不会脱离轨道).

a.分析A沿轨道下滑到任意一点的动量p_A与B平抛经过该点的动量p_B的大小关系；

b.在OD曲线上有一M点，O和M两点连线与竖直方向的夹角为45°.求A通过M点时的水平分速度和竖直分速度.

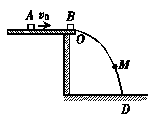[2008年高考·北京理综卷]

解析：(1)滑块A与B正碰，有：

mv₀＝mv_A+mv_B

mv＝mv+mv

解得：v_A＝0，v_B＝v₀，

根据动量定理，滑块B满足：F·Δt＝mv₀

解得：F＝.

(2)a.设任意点到O点竖直高度差为d.

A、 B由O点分别运动至该点过程中，只有重力做功，所以机械能守恒.

选该任意点为势能零点，有：

E_kA＝mgd，E_kB＝mgd+mv

由于p＝，有＝＝＜1

即p_A<p_B

A下滑到任意一点的动量总是小于B平抛经过该点的动量.

b.以O为原点，建立直角坐标系xOy，x轴正方向水平向右，y轴正方向竖直向下，则对B有：

x＝v₀t

y＝gt²

B的轨迹方程：y＝·x²

在M点x＝y，所以y＝

因为A、B的运动轨迹均为OD曲线，故在任意一点，两者速度方向相同.设B水平和竖直分速度大小分别为v_Bx和v_By，速率为v_B；A水平和竖直分速度大小分别为v_Ax和v_Ay，速率为v_A，则：

＝，＝

B做平抛运动，故

v_Bx＝v₀，y_By＝，v_B＝

对A由机械能守恒得v_A＝

由以上三式解得：v_Ax＝，v_Ay＝

将代y＝入得：v_Ax＝v₀，v_Ay＝v₀.

　答案：(1)　(2)a.p_A＜p_B　b.v₀，v₀

10.神奇的黑洞是近代引力理论所预言的一种特殊天体，探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时，发现了LMCX－3双星系统，如图所示，它由可见星A和不可见的暗星B构成.两星视为质点，不考虑其他天体的影响，A、B围绕两者连线上的O点做匀速圆周运动，它们之间的距离保持不变.引力常量为G，由观测能够得到可见星 A的速率 v和运行周期 T.

(1)可见星A所受暗星 B的引力 F_A 可等效为位于 O点处质量为m′的星体(视为质点)对它的引力，设A和B的质量分别为 m₁、m₂，试求m′. (用m₁、m₂ 表示)

(2)求暗星B的质量m₂ 与可见星A的速率v、运行周期T和质量m₁ 之间的关系式.

(3)恒星演化到末期，如果其质量大于太阳质量m_s 的2倍，它将有可能成为黑洞.若可见星A的速率v＝2.7×10⁵ m/s，运行周期T＝4.7π×10⁴ s，质量m₁＝6m_s，试通过估算来判断暗星B有可能是黑洞吗？ (G＝6.67×10^－11　 N·m²/kg²，m_s＝2.0×10³⁰ kg)[2006年高考·天津理综卷]

解析：(1)设 A、B的圆轨道半径分别为 r₁、 r₂ ，由题意知，A、B做匀速圆周运动的角速度相同，设其为ω.由牛顿运动定律，有：

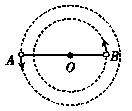F_A＝m₁ ω²r₁

F_B＝m₂ω²r₂

F_A＝F_B

设A、B之间的距离为r，又r＝r₁+r₂，由上述各式得：

r＝r₁

由万有引力定律，有：

F_A＝G

联立解得：F_A＝G

令F_A＝G

比较可得：m′＝.

　(2)由牛顿第二定律，有：

　G＝m₁

可见星A的轨道半径r₁＝

将m′代入，可解得：＝.

(3)将m₁＝6m_s代入上式，得：

＝

代入数据得：＝3.5m_s

设m₂＝nm_s(n>0)，可得：

＝m_s＝3.5m_s

可见，的值随n的增大而增大，试令n＝2，得：

m_s＝0.125m_s<3.5m_s

故n必大于2，即暗星B的质量m₂必大于2m_s.由此得出结论：暗星B有可能是黑洞.

　答案：(1)　(2)＝

(3)有可能

9.如图所示是一种叫“飞椅”的游乐项目的示意图，长为L的钢绳一端系着座椅，另一端固定在半径为r的水平转盘边缘，转盘可绕穿过其中心的竖直轴转动.当转盘以角速度ω匀速转动时，钢绳与转轴在同一竖直平面内，与竖直方向的夹角为θ，不计钢绳的重力，求转盘转动的角速度ω与夹角θ的关系.[2008年高考·广东物理卷]

解析：设转盘转动角速度为ω，夹角为θ，则

座椅到做圆周运动的半径R＝r+Lsin θ

对座椅有：F_向心＝mgtan θ＝mRω²

联立两式解得：ω＝.

　答案：