
6.一辆值勤的警车停在公路边,当警员发现从他旁边以10 m/s的速度匀速行驶的货车严重超载时,决定前去追赶.经过5.5 s后警车发动起来,并以2.5 m/s2的加速度做匀加速运动,但警车的行驶速度必须控制在90 km/h以内.问:
(1)警车在追赶货车的过程中,两车间的最大距离是多少?
(2)警车发动后要多长时间才能追上货车?
解析:解法一 (1)警车在追赶货车的过程中,当两车的速度相等时,它们之间的距离最大.设警车发动后经过t1时间两车的速度相等,则:
t1= s=4 s
s货=(5.5+4)×10 m=95 m
s警=at=×2.5×42 m=20 m
所以两车间的最大距离Δs=s货-s警=75 m.
(2)vm=90 km/h=25 m/s,当警车刚达到最大速度时,运动时间t2= s=10 s
s货′=(5.5+10)×10 m=155 m
s警′=at=×2.5×102 m=125 m
因为s货′>s警′,故此时警车尚未赶上货车,且此时两车间的距离Δs′=s货′-s警′=30 m
警车达到最大速度后做匀速运动,设再经过Δt时间追赶上货车,则:
Δt==2 s所以警车发动后追上货车要经过的时间为:
t=t2+Δt=12 s.
解法二 (1)在v-t图象中,两车的运动图线如图所示.因为位移等于v-t图象与t轴所围成的面积,由此可知在t1=9.5 s时两车间的距离最远.
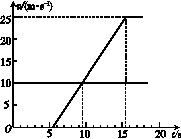 此时:Δsm=v0·t1-a(t1-t0)2=75 m.
此时:Δsm=v0·t1-a(t1-t0)2=75 m.
(2)由图象可知,警车加速t2==10 s时间后达到最大速度.
设警车发动后经t时间追上货车,由图象的意义可知:
v0(t0+t)=at+vm·(t-t2)
解得:t=12 s.
答案:(1)75 m (2)12 s
金典练习五 自由落体运动 竖直上抛运动 运动图象 追赶问题
选择题部分共10小题,每小题6分.在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.
5.一玩具火车A的制动性能经如下测定:当它以0.2 m/s 的速度在水平平直轨道上行驶时,在制动后需要40 s才能停下.现这列玩具火车正以0.2 m/s的速度在水平轨道上行驶,在其侧前方相距75 cm处有另一玩具火车B正以0.06 m/s 的速度在一旁的平行轨道上同向行驶.现对玩具火车A采取制动措施,问:两车是否会发生会车?会车几次?会车发生在什么时刻?
对于上述问题,小王同学是这样认为的:
两玩具火车相遇时,有:sA=sB
sB=0.75+0.06t
sA=0.2t-
即0.75+0.06t=0.2t-
解上述方程组,得到本题的结果.因为是二次方程,有两个解,故两小车会车两次.
小王同学的理解正确吗?如果你认为他的理解是正确的,那就请你解出相遇的时间;如果你认为他的理解有问题,那就请你给出简要的分析说明,并给出你的结果.
解析:该同学的结论是错误的.
由0.75+0.06t=0.2t-
解得:t1=6 s,t2=50 s
玩具火车A在40 s时已经停下,t2=50 s不合理,舍去.
玩具火车A停下时距离其出发点s1= t=·t=4 m
火车B到达该位置所需的时间为:
t2== s=54.17 s
即两车相会两次,分别为:t1=6 s,t2=54.17 s.
答案:两车相会两次,分别在t1=6 s和t2=54.17 s时刻
4.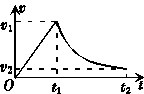 在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达较大值v1时打开降落伞做减速运动,在t2时刻以较小的速度v2着地.他的速度图象如图所示.下列关于该空降兵在0-t2或t1-t2时间内的平均速度的结论中,正确的是( )
在军事演习中,某空降兵从飞机上跳下,先做自由落体运动,在t1时刻,速度达较大值v1时打开降落伞做减速运动,在t2时刻以较小的速度v2着地.他的速度图象如图所示.下列关于该空降兵在0-t2或t1-t2时间内的平均速度的结论中,正确的是( )
A.0-t2时间内=
B.t1-t2时间内=
C.t1-t2时间内>
D.t1-t2时间内<
解析:在0-t1时间内1=
在t1-t2时间内2<
故选项B、C错误、D正确.
对于0-t2时间内的平均速度,有<、=和>三种可能,无法判定二者的关系,故选项A错误.
答案:D
3.两辆游戏赛车a、b在两条平行的直车道上行驶.t=0时两车都在同一计时线处,此时比赛开始.它们的四次比赛中的v-t图象如图所示.下列图象对应的比赛中,有一辆赛车追上了另一辆的是[2007年高考·海南物理卷]( )
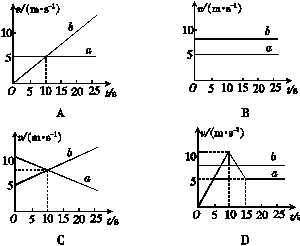
解析:在A、C图象中,在t=20 s时刻b车追上a车.
答案:AC
2.下列给出的四组图象中,能够反映同一直线运动的是( )
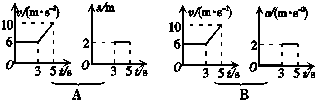
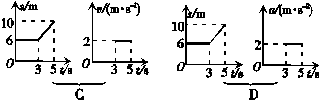
答案:BC
1.甲、乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标.在描述两车运动的v-t图象中(如图所示),直线a、b分别描述了甲、乙两车在0-20 s的运动情况.关于两车之间的位置关系,下列说法正确的是[2007年高考·宁夏理综卷]( )
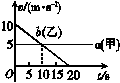
A.在0-10 s内两车逐渐靠近
B.在10-20 s内两车逐渐远离
C.在5-15 s内两车的位移相等
D.在t=10 s时两车在公路上相遇
答案:C
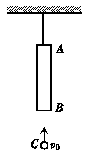
5.如图所示,长为0.5 m的圆筒AB悬挂于天花板上,在AB的正下方有直径小于圆筒内径的小钢球C,C距圆筒下端B的距离h=2 m.某时刻烧断悬挂AB的悬绳,同时将小钢球C以v0=20 m/s的初速度竖直上抛.空气阻力不计,取g=10 m/s2,求小钢球C从圆筒AB中穿过的时间.
解析:解法一 取C上抛位置处为位移参考点,向上为正方向,则:
 sA=h+l-gt2
sA=h+l-gt2
sB=h-gt2
sC=v0t-gt2
故C与B相遇的时刻有:sB=sC
解得:t1==0.1 s
C与A相遇的时刻有:sA=sC
解得:t2==0.125 s
故C从AB中穿过的时间Δt=t2-t1=0.025 s.
解法二 考虑圆筒与钢球的速度,则:
vAB=-gt,vC=v0-gt
故它们的相对速度v相=vC-vAB=v0
所以C从AB中穿过的时间Δt==0.025 s.
答案:0.025 s
第11讲 运动图象 追赶问题
体验成功
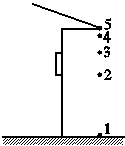
4.屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴恰好到达地面,而第3滴与第2滴分别位于高为1 m的窗户的上下缘,如图所示.取g=10 m/s2,问:
(1)此屋檐离地面多高?
(2)滴水的时间间隔是多少?
解析:(1)可以将这5滴水的运动等效地视为一滴水的下落,并对这一滴水的运动全过程分成4个相等的时间间隔,图中相邻的两滴水间的距离分别对应着各个相等时间间隔内的位移,它们满足比例关系:1∶3∶5∶7.设相邻水滴之间的距离自上而下依次为:x、3x、5x、7x,则窗户高为5x,依题意有5x=1 m,则x=0.2 m.
屋檐高度h=x+3x+5x+7x=16x=3.2 m.
(2)由h=gt2
得:t== s=0.8 s
所以滴水的时间间隔Δt==0.2 s.
答案:(1)3.2 m (2)0.2 s
3.在地质、地震、勘探、气象和地球物理等领域的研究中,需要精确的重力加速度g值,g值可由实验精确测定.近年来测g值的一种方法叫“对称自由下落法”,它是将测g值归于测长度和时间,以稳定的氦氖激光的波长为长度标准,用光学干涉的方法测距离,以铷原子钟或其他手段测时间,此方法能将g值测得很准.具体做法是:将真空长直管沿竖直方向放置,自其中的O点向上抛小球,从抛出小球至小球又落回抛出点的时间为T2;小球在运动过程中经过比O点高H的P点,小球离开P点至又回到P点所用的时间为T1.由T1、T2和H的值可求得g等于( )
A. B.
 C. D.
C. D.
解析:设小球上升的最大高度为h,由题意知:
h=g()2
h-H=g()2
解得:g=.
答案:A
2.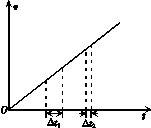 两个小球分别拴在一根轻绳的两端,一人用手拿住一球将它们从三楼阳台上由静止释放,两球先后落地的时间差为Δt1;若将它们从四楼阳台上由静止释放,则它们落地的时间差为Δt2.不计空气阻力,则Δt1、Δt2满足( )
两个小球分别拴在一根轻绳的两端,一人用手拿住一球将它们从三楼阳台上由静止释放,两球先后落地的时间差为Δt1;若将它们从四楼阳台上由静止释放,则它们落地的时间差为Δt2.不计空气阻力,则Δt1、Δt2满足( )
A.Δt1=Δt2 B.Δt1<Δt2
C.Δt1>Δt2 D.以上都有可能
解析:时间差等于轻绳长度除以下面小球落地后上面小球运动的平均速度,故Δt1>Δt2.
答案:C
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com