3.(10分)图示为气垫导轨上两个滑块A、B相互作用后运动过程的频闪照片.频闪的频率为10 Hz.开始两个滑块静止，它们之间有一根被压缩的轻弹簧，滑块用绳子连接，绳子烧断后，两个滑块向相反方向运动.已知滑块A、B的质量分别为200 g、300 g.根据照片记录的信息，A、B离开弹簧后，A滑块做　　运动，其速度大小为　　，本实验得出“在实验误差范围内，两木块组成的系统动量守恒”这一结论的依据是：

　　　　　　　　　　　　　　　　　　　　　　.

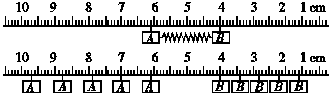
答案：匀速　0.09 m/s　释放弹簧前A、B的总动量为零；释放后p_A＝0.2×0.09 N·s＝1.8×10^－2 N·s，p_B＝－0.3× N·s＝－1.8×10^－2 N·s，p_A+p_B＝0

2.某同学利用计算机模拟A、B两球碰撞来验证动量守恒，已知A、B两球质量之比为2∶3，用A球作入射球，初速度v₁＝1.2 m/s，让A球与静止的B球相碰，若规定以v₁的方向为正，则该同学记录碰后的数据中，明显不合理的是(　)

解析：由动量守恒定律和能量的转化和守恒定律知，实验数据在误差允许范围内应满足：

m₁v₁＝m₁v₁′+m₂v₂′

m₁v≥m₁v₁′²+m₂v₂′²

又由两球的位置关系知：v₁′≤v₂′

可得B、C中数据不合理.

答案：BC

非选择题部分共7小题，共88分.

1.在做“验证动量守恒定律”的实验时，需要测定的物理量有(　)

A.小球的质量　　　B.小球的半径

C.小球的飞行时间　 D.小球的水平射程

答案：AD

3.为了验证碰撞中的动量守恒和检验两个小球的碰撞是否为弹性碰撞(即碰撞过程中没有机械能损失)，某同学选取了两个体积相同、质量不相等的小球按下述步骤做了如下实验.

a.用天平测出两个小球1、2的质量(分别为m₁和m₂，且m₁>m₂).

b.按照图示安装好实验装置：将斜槽AB固定在桌边，使槽的末端点的切线水平，将一斜面BC连接在斜槽末端.

c.先不放小球2，让小球1从斜槽顶端的A处由静止开始滚下，记下小球在斜面上的落点位置.

d.将小球2放在斜槽前端边缘处，让小球1从斜槽顶端的A处滚下，使它们发生碰撞，记下小球1和小球2在斜面上的落点位置.

e.用毫米刻度尺量出各个落点位置到斜槽末端点B的距离.

图中D、E、F点是该同学记下的小球在斜面上的几个落点位置，到B点的距离分别为L_D、L_E、L_F.

根据该同学的实验，回答下列问题：

(1)小球1与2发生碰撞后，1的落点是图中的　　　点，2的落点是图中的　　点.

(2)用测得的物理量来表示，只要满足关系式　　　　　　，则说明碰撞中动量是守恒的.

(3)用测得的物理量来表示，只要再满足关系式　　　　　　，则说明两小球的碰撞是弹性碰撞.

解析：设斜面的倾角为θ，小球做平抛运动，由Lsin θ＝gt²、Lcos θ＝vt，得其抛出速度v ∝；验证动量是否守恒的表达式为m₁v₀＝m₁v₁+m₂v₂，即m₁＝m₁+m₂；若没有机械能损失，则m₁v＝m₁v+m₂v，代入v ∝，得m₁L_E＝m₁L_D+m₂L_F.

答案：(1)D　F

(2)m₁＝m₁+m₂

(3)m₁L_E＝m₁L_D+m₂L_F

金典练习十八　实验：验证动量守恒定律

选择题部分共2小题，每小题6分.在每小题给出的四个选项中，有的小题只有一个选项正确，有的小题有多个选项正确.

2.如图所示，在实验室用两端带竖直挡板C、D的气垫导轨和有固定挡板的质量都是M的滑块A、B做“验证动量守恒定律”的实验，实验步骤如下：

a.把两滑块A、B紧贴在一起，在A上放质量为m的砝码，置于导轨上，用电动卡销卡住A、B，在A、B的固定挡板间放入一弹簧，使弹簧在水平方向上处于压缩状态.

b.按下电钮使电动卡销放开，同时启动记录两滑块运动时间的电子计时器，当滑块A、B与挡板C、D碰撞的同时，电子计时器自动停止计时，记下A至C的运动时间t₁和B至D的运动时间t₂.

c.将两滑块A、B仍置于原位置，重复几次上述实验，并对多次实验记录的t₁、t₂分别取平均值.

(1)在调整气垫导轨时，应注意　.

(2)应测量的数据还有　.

(3)只要满足关系式　　　　，即可验证动量守恒.

解析：由于滑块和气垫导轨间的摩擦力很小，可以忽略不计，可认为滑块在导轨上做匀速直线运动，因此两滑块作用后的速度可分别表示为：v_A＝，v_B＝.

若(M+m)＝M成立，则(M+m)v_A＝Mv_B成立，即动量守恒.

答案：(1)用水平仪测量使导轨水平　(2)A至C板的距离L₁，B至D板的距离L₂　(3)(M+m)＝M

1.实验“验证动量守恒定律”的主要步骤为：

A.测出球的直径和质量m₁、m₂，若m₁<m₂，则用质量为m₂的球作为入射球

B.把被碰球放在斜槽末端，让入射球从斜槽上同一高度滚下，与被碰球做正碰，重复多次，找出落点的平均位置

C.使入射球从斜槽上某一固定高度滚下，重复多次，找出落点的平均位置

D.测出入射球碰撞前后落点的水平距离和被碰球落点的水平距离

E.调整斜槽末端，使槽口的切线水平

以上步骤合理的排列顺序是　　　.

答案：AECBD

13.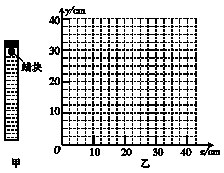(14分)如图甲所示，在一端封闭、长约1 m的玻璃管内注满清水，水中放一蜡块，将玻璃管的开口端用胶塞塞紧，然后将这个玻璃管倒置，在蜡块沿玻璃管上升的同时 ，将玻璃管水平向右移动.假设从某时刻开始计时，蜡块在玻璃管内每1 s上升的距离都是10 cm，玻璃管向右匀加速平移，连续的每1 s通过的水平位移依次是2.5 cm、7.5 cm、12.5 cm、17.5 cm.图乙中，y表示蜡块竖直方向的位移，x表示蜡块随玻璃管通过的水平位移，t＝0时蜡块位于坐标原点.

(1)请在图乙中描绘出蜡块4 s内的轨迹.

(2)求出玻璃管向右平移的加速度a.

(3)求t＝2 s时蜡块的速度v2.

解析：(1)蜡块4 s内的轨迹如图丙所示.

(2)由蜡块的运动轨迹知，蜡块在水平方向的分运动为匀加速运动，在竖直方向的分运动为匀速运动，故加速度：

a＝＝ m/s2＝5×10－2 m/s2.

(3)蜡块在竖直方向的速度vy＝＝0.1 m/s

t＝2 s时刻蜡块水平方向的分速度为：

vx＝at＝0.1 m/s

故v2＝＝0.14 m/s

方向与水平、竖直正方向均成45°角.

答案：(1)如图丙所示

(2)a＝5×10－2 m/s2

(3)v2＝0.14 m/s，方向与水平、竖直正方向均成45°角

12.(13分)如图甲所示，墙壁上落有两只飞镖，它们是从同一位置水平射出的.飞镖A与竖直墙壁成53°角，飞镖B与竖直墙壁成37°角，两者相距d.假设飞镖的运动是平抛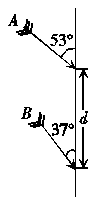运动，试估算射出点离墙壁的水平距离.(假设飞镖与墙壁的夹角等于镖的速度方向与竖直方向的夹角，已知sin 37°＝0.6，cos 37°＝0.8.)

解析：解法一　设射击点离墙壁的水平距离为x，两飞镖的初速度分别为vA、vB，则：

飞镖A的飞行时间tA＝＝

解得：tA＝

飞镖B的飞行时间tB＝＝

解得：tB＝

又由A、B竖直方向的位移关系可得：

d＝g·t－gt

可解得：x＝d.

解法二　平抛运动的速度与水平方向的夹角θ、位移与水平方向的夹角为α，如图乙所示，有：

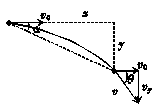tan θ＝

tan α＝＝＝tan θ

由此可知若飞镖A的位移与水平方向的夹角为α1，有：

tan α1＝tan 37°＝

若飞镖B的位移与水平方向的夹角为α2，有：

tan α2＝tan 53°＝

故飞镖A的竖直位移yA＝x·tan α1

飞镖B的竖直位移yB＝x·tan α2＝yA+d

可解得：x＝d.

答案：x＝d

11.(13分)如图所示，光滑斜面的倾角为θ，斜边长为L，斜面顶端有一小球以平行底边的速度v0水平抛出.则小球滑到底端时，水平方向的位移多大？

解析：将小球的运动分解为以下两个分运动：

①小球在水平方向不受力，做匀速直线运动.

②沿斜面向下做初速度为零的匀加速直线运动，加速度为gsin θ.

合运动为类平抛运动.则在水平方向上有：s＝v0t

在沿斜面向下有：L＝at2

由牛顿第二定律有：mgsin θ＝ma

联立解得：s＝v0.

答案：v0

10.从某一高度以相同速度相隔1 s先后水平抛出甲、乙两个小球.不计空气阻力，在乙球抛出后两球在空中运动的过程中，下列说法正确的是(　)

A.两球水平方向的距离越来越大

B.两球竖直高度差越来越大

C.两球水平方向的速度差越来越大

D.两球每秒内的速度变化量相同，与其质量无关

解析：两球做匀加速运动的加速度相等，都为g，两球每秒速度的变化都相同，D正确.取乙球抛出时刻及位置为零时刻和零位移，甲、乙两球的位移和速度分别如下：

甲球的速度　乙球的速度

甲球的位移　乙球的位移

故知A、C错误，B正确.

答案：BD

非选择题部分共3小题，共40分.