
第一节 单项填空(共15小题;每小题1分,满分15分)
从每题所给的A、B、C、D四个选项中,选出可以填入空白处的最佳选择。并在答题卡上将该项涂黑。
21. I remember seeing this kind of _____ product in _____ city of Shanghai, which is
known as _____ Paris of the East.
A. the; the; the B. /; the; the C. the; /; the D. the; a; /
4. 已知直线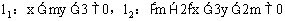 。
。
当m为_______时,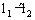 ;
;
当m为_______时,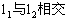 ;
;
当m为_______时, 。
。
3. 求直线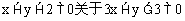 对称的直线方程。
对称的直线方程。
2. 直线l经过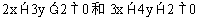 的交点,且与两坐标轴围成等腰直角三角形,求直线l的方程。
的交点,且与两坐标轴围成等腰直角三角形,求直线l的方程。
1. 已知: ,求实数m值使得:
,求实数m值使得:
(1)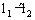 ;(2)
;(2) ;(3)
;(3)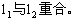
3. 点到直线的距离公式:设已知点P(x0,y0),直线l的方程为:Ax+By+C=0,
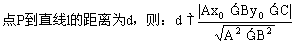
例1. 在等腰Rt△ABC中,∠C=90°,直角边BC在直线2x+3y-6=0上,顶点A(5,4),求AB和AC所在的直线方程。
解析:

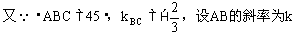
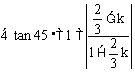
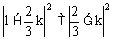


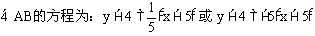
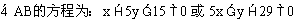
例2. 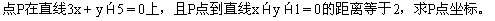
解: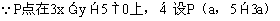
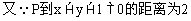
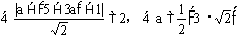
例3. 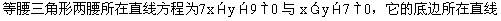
通过A(3,-8),求底边所在的直线方程。
解析:根据等腰三角形的两个底角相等,由此等量关系,根据到角公式即可求出底边的斜率。
解:设底边的斜率为k

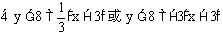

例4. 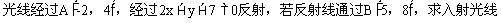
与反射光线所在的直线方程。
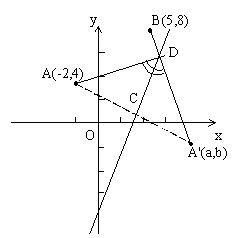
分析:根据入射角等于反射角知识,可知:点A的对称点A'应在反射光线上,连结A'B交已知直线于D,则AD为入射线,则任务为求A'B和AD的方程。
解: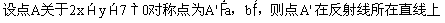


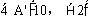
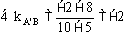
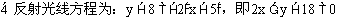
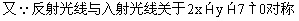
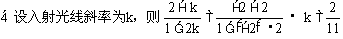
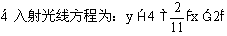
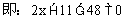
例5. 证明:三点A(1,3),B(5,7),C(10,12)共线。
分析:可采取其中一点到过另两点的直线的距离为0来证明。
证明:
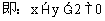


说明:证三点共线:
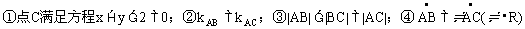
[模拟试题]
2. 两个公式:



1. 两个概念:
(1)l1到l2的角:
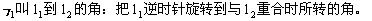
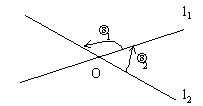
(2)l1与l2的夹角:
在l1到l2和l2到l1的角中,那个不大于90°的角叫做l1与l2的夹角。
注:①当l1与l2斜交时,夹角为锐角;
②当l1⊥l2时,夹角为90°;
③当l1∥l2时,夹角是0°。
夹角的范围:[0°,90°]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com