
3. 一只沿垂直于河岸的方向,以恒定的速度渡河,当船运动到河中央时,河水的流速突然增大,则船渡河的时间将
A.增大 B.不变 C.减小 D.无法确定
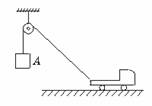
2. 如图所示,在不计滑轮摩擦和绳子质量的条件下,当小车匀速向右运动时,物体A的受力情况是
A.绳的拉力大于A的重力
B.绳的拉力等于A的重力
C.绳的拉力小于A的重力
D.拉力先大于重力,后变为小于重力
1.关于互成角度的两个初速度不为零的匀变速直线运动的合运动,下述说法正确的是
A.一定是直线运动
B.一定是抛物线运动
C.可能是直线运动,也可能是抛物线运动
 D.以上说法都不对
D.以上说法都不对
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
提出问题 |
示例1:数集的拓展 示例2:方程(x – 2) (x2 – 3) = 0的解集. ①在有理数范围内,②在实数范围内. |
学生思考讨论. |
挖掘旧知,导入新知,激发学习兴趣. |
|
形成概念 |
1.全集的定义. 如果一个集合含有我们所研究问题中涉及的所有元素,称这个集合为全集,记作U.  示例3:A = {全班参加数学兴趣小组的同学},B = {全班设有参加数学兴趣小组的同学},U = {全班同学},问U、A、B三个集关系如何.  2.补集的定义  补集:对于一个集合A,由全集U中不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,记作  UA. UA. 即  UA = {x | x∈U,且 UA = {x | x∈U,且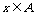 }, }, Venn图表示    |
师:教学学科中许多时候,许 多问题都是在某一范围内进行研究. 如实例1是在实数集范围内不断扩大数集. 实例2:①在有理数范围内求解;②在实数范围内求解. 类似这些给定的集合就是全集. 师生合作,分析示例  生:①U = A∪B,  ②U中元素减去A中元素就构成B.  师:类似②这种运算得到的集合B称为集合A的补集,生师合作交流探究补集的概念. |
合作交流,探究新知,了解全集、补集的含义. |
应用举例 深化概念 |
例1 设U = {x | x是小于9的正整数},A = {1,2,3},B = {3,4,5,6},求 UA, UA, UB. UB. 例2 设全集U = {x | x是三角形},A = {x|x是锐角三角形},B = {x | x是钝角三角形}. 求A∩B,  U (A∪B). U (A∪B). |
学生先尝试求解,老师指导、点评. 例1解:根据题意可知,U = {1,2,3,4,5,6,7,8},所以  UA = {4, 5, 6, 7, 8}, UA = {4, 5, 6, 7, 8},  UB = {1, 2, 7, 8}. UB = {1, 2, 7, 8}. 例2解:根据三角形的分类可知 A∩B = 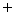 , , A∪B = {x | x是锐角三角形或钝角三角形},   U (A∪B) = {x | x是直角三角形}. U (A∪B) = {x | x是直角三角形}. |
加深对补集概念的理解,初步学会求集合的补集. |
|
性质探究 |
补集的性质: ①A∪(  UA) = U, UA) = U, ②A∩(  UA) = UA) =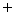 . . 练习1:已知全集U = {1, 2, 3, 4, 5, 6, 7},A={2, 4, 5},B = {1, 3, 5, 7},求A∩(  UB),( UB),( UA)∩( UA)∩( UB). UB). 总结:  (  UA)∩( UA)∩( UB) = UB) =  U (A∪B), U (A∪B), (  UA)∪( UA)∪( UB) = UB) =  U (A∩B). U (A∩B). |
师:提出问题 生:合作交流,探讨  师生:学生说明性质①、②成立的理由,老师点评、阐述.  师:变式练习:求A∪B,求  U (A∪B)并比较与( U (A∪B)并比较与( UA)∩( UA)∩( UB)的结果. UB)的结果.  解:因为  UA = {1, 3, 6, 7}, UA = {1, 3, 6, 7}, UB = {2, 4, 6},所以A∩( UB = {2, 4, 6},所以A∩( UB) = {2, 4}, UB) = {2, 4}, (  UA)∩( UA)∩( UB) = {6}. UB) = {6}. 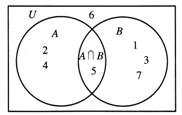 |
能力提升. 探究补集的性质,提高学生的归纳能力. |
|
应用举例 |
例2 填空 (1)若S = {2,3,4},A = {4,3},则  SA = . SA = . (2)若S = {三角形},B = {锐角三角形},则  SB = . SB = . (3)若S = {1,2,4,8},A = 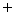 ,则 ,则 SA = . SA = . (4)若U = {1,3,a2 + 3a + 1},A = {1,3},  UA = {5},则a . UA = {5},则a . (5)已知A = {0,2,4},  UA = {–1,1}, UA = {–1,1}, UB = {–1,0,2},求B = UB = {–1,0,2},求B = .  (6)设全集U = {2,3,m2 + 2m – 3},A = {|m + 1| ,2},  UA = {5},求m. UA = {5},求m. (7)设全集U = {1,2,3,4},A = {x | x2 – 5x + m = 0,x∈U},求  UA、m. UA、m. |
师生合作分析例题. 例2(1):主要是比较A及S的区别,从而求  SA . SA .例2(2):由三角形的分类找B的补集. 例2(3):运用空集的定义. 例2(4):利用集合元素的特征. 综合应用并集、补集知识求解. 例2(7):解答过程中渗透分类讨论思想. 例2(1)解:  SA = {2} SA = {2}例2(2)解:  SB = {直角三角形或钝角三角形} SB = {直角三角形或钝角三角形}例2(3)解:  SA = S SA = S 例2(4)解:a2 + 3a + 1 = 5, a = – 4或1. 例2(5)解:利用韦恩图由A设  UA 先求U = {–1,0,1,2,4},再求B = {1,4}. UA 先求U = {–1,0,1,2,4},再求B = {1,4}.例2(6)解:由题m2 + 2m – 3 = 5且|m + 1| = 3, 解之m = – 4或m = 2. 例2(7)解:将x = 1、2、3、4代入x2 – 5x + m = 0中,m = 4或m = 6, 当m = 4时,x2 – 5x + 4 = 0,即A = {1,4}, 又当m = 6时,x2 – 5x + 6 = 0,即A = {2,3}. 故满足条件:  UA = {1,4},m = 4; UA = {1,4},m = 4; UB = {2,3},m = 6. UB = {2,3},m = 6. |
进一步深化理解补集的概念. 掌握补集的求法. |
|
归纳总结 |
1.全集的概念,补集的概念. 2.  UA ={x | x∈U,且 UA ={x | x∈U,且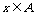 }. }.3.补集的性质: ①(  UA)∪A = U,( UA)∪A = U,( UA)∩A = UA)∩A =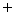 , ,②  U U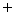 = U, = U, UU = UU =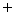 , ,③(  UA)∩( UA)∩( UB) = UB) =  U (A∪B), U (A∪B),(  UA)∪( UA)∪( UB) = UB) =  U (A∩B) U (A∩B) |
师生合作交流,共同归纳、总结,逐步完善. |
引导学生自我回顾、反思、归纳、总结,形成知识体系. |
|
课后作业 |
1.1 第四课时习案 |
学生独立完成 |
巩固基础、提升能力 |
备选例题
例1 已知A = {0,2,4,6}, SA = {–1,–3,1,3},
SA = {–1,–3,1,3}, SB = {–1,0,2},用列举法写出集合B.
SB = {–1,0,2},用列举法写出集合B.
[解析]∵A = {0,2,4,6}, SA = {–1,–3,1,3},
SA = {–1,–3,1,3},
∴S = {–3,–1,0,1,2,3,4,6}
而 SB = {–1,0,2},∴B =
SB = {–1,0,2},∴B = S (
S ( SB) = {–3,1,3,4,6}.
SB) = {–3,1,3,4,6}.
例2 已知全集S = {1,3,x3 +
3x2 + 2x},A = {1,|2x – 1|},如果 SA = {0},则这样的实数x是否存在?若存在,求出x;若不存在,请说明理由.
SA = {0},则这样的实数x是否存在?若存在,求出x;若不存在,请说明理由.
[解析]∵ SA = {0},∴0∈S,但0
SA = {0},∴0∈S,但0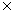 A,∴x3 +
3x2 + 2x = 0,x(x + 1) (x + 2) = 0,
A,∴x3 +
3x2 + 2x = 0,x(x + 1) (x + 2) = 0,
即x1 = 0,x2 = –1,x3 = –2.
当x = 0时,|2x – 1| = 1,A中已有元素1,不满足集合的性质;
当x= –1时,|2x – 1| = 3,3∈S; 当x = –2时,|2x – 1| = 5,但5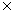 S.
S.
∴实数x的值存在,它只能是–1.
例3 已知集合S = {x | 1<x≤7},A = {x | 2≤x<5},B = {x | 3≤x<7}. 求:
(1)( SA)∩(
SA)∩( SB);(2)
SB);(2) S (A∪B);(3)(
S (A∪B);(3)( SA)∪(
SA)∪( SB);(4)
SB);(4) S (A∩B).
S (A∩B).
[解析]如图所示,可得
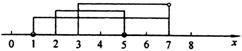
A∩B = {x | 3≤x<5},A∪B = {x | 2≤x<7},
 SA = {x | 1<x<2,或5≤x≤7},
SA = {x | 1<x<2,或5≤x≤7}, SB = {x | 1<x<3}∪{7}.
SB = {x | 1<x<3}∪{7}.
由此可得:(1)( SA)∩(
SA)∩( SB) = {x | 1<x<2}∪{7};
SB) = {x | 1<x<2}∪{7};
(2) S (A∪B) = {x | 1<x<2}∪{7};
S (A∪B) = {x | 1<x<2}∪{7};
(3)( SA)∪(
SA)∪( SB) = {x | 1<x<3}∪{x |5≤x≤7} = {x | 1<x<3,或5≤x≤7};
SB) = {x | 1<x<3}∪{x |5≤x≤7} = {x | 1<x<3,或5≤x≤7};
(4) S (A∩B) = {x | 1<x<3}∪{x | 5≤x≤7} = {x | 1<x<3,或5≤x≤7}.
S (A∩B) = {x | 1<x<3}∪{x | 5≤x≤7} = {x | 1<x<3,或5≤x≤7}.
例4 若集合S = {小于10的正整数},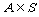 ,
,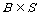 ,且(
,且( SA)∩B = {1,9},A∩B = {2},(
SA)∩B = {1,9},A∩B = {2},( SA)∩(
SA)∩( SB) = {4,6,8},求A和B.
SB) = {4,6,8},求A和B.
[解析]由( SA)∩B = {1,9}可知1,9
SA)∩B = {1,9}可知1,9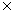 A,但1,9∈B,
A,但1,9∈B,
由A∩B = {2}知,2∈A,2∈B.
由( SA)∩(
SA)∩( SB) = {4,6,8}知4,6,8
SB) = {4,6,8}知4,6,8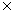 A,且4,6,8
A,且4,6,8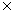 B
B
下列考虑3,5,7是否在A,B中:
若3∈B,则因3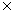 A∩B,得3
A∩B,得3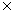 A.
于是3∈
A.
于是3∈ SA,所以3∈(
SA,所以3∈( SA)∩B,
SA)∩B,
这与( SA)∩B = {1,9}相矛盾.
SA)∩B = {1,9}相矛盾.
故3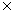 B,即3∈(
B,即3∈( SB),又∵3
SB),又∵3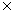 (
( SA)∩(
SA)∩( SB),
SB),
∴3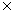 (
( SA),从而3∈A;同理可得:5∈A,5
SA),从而3∈A;同理可得:5∈A,5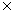 B;7∈A,7
B;7∈A,7 B.
B.
故A = {2,3,5,7},B = {1,2,9}.
评注:此题Venn图求解更易.
通过示例,尝试发现式学习法;通过示例的分析、探究,培养发现探索一般性规律的能力.
重点:补集概念的理解;难点:有关补集的综合运算.
3.情感、态度与价值观
通过补集概念的形成与发展、理解与掌握,感知事物具有相对性,渗透相对的辨证观点.
2.过程与方法
通过示例认识全集,类比实数的减法运算认识补集,加深对补集概念的理解,完善集合运算体系,提高思维能力.
1.知识与技能
(1)了解全集的意义.
(2)理解补集的含义,会求给定子集的补集.
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
|
提出问题引入新知 |
思考:观察下列各组集合,联想实数加法运算,探究集合能否进行类似“加法”运算. (1)A = {1,3,5},B = {2,4,6},C = {1,2,3,4,5,6}  (2)A = {x | x是有理数},  B = {x | x是无理数},  C = {x | x是实数}. |
师:两数存在大小关系,两集合存在包含、相等关系;实数能进行加减运算,探究集合是否有相应运算. 生:集合A与B的元素合并构成C.  师:由集合A、B元素组合为C,这种形式的组合就是为集合的并集运算. |
生疑析疑, 导入新知 |
形成 概念 |
思考:并集运算. 集合C是由所有属于集合A或属于集合B的元素组成的,称C为A和B的并集.  定义:由所有属于集合A或集合B的元素组成的集合. 称为集合A与B的并集;记作:A∪B;读作A并B,即A∪B = {x | x∈A,或x∈B},Venn图表示为:  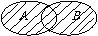  |
师:请同学们将上述两组实例的共同规律用数学语言表达出来. 学生合作交流:归纳→回答→补充或修正→完善→得出并集的定义. |
在老师指导下,学生通过合作交流,探究问题共性,感知并集概念,从而初步理解并集的含义. |
|
应用举例 |
例1 设A = {4,5,6,8},B = {3,5,7,8},求A∪B.  例2 设集合A = {x | –1<x<2},集合B = {x | 1<x<3},求A∪B.  |
例1解:A∪B = {4, 5, 6, 8}∪{3, 5, 7, 8} = {3, 4, 5, 6, 7, 8}. 例2解:A∪B = {x |–1<x<2}∪{x|1<x<3} = {x = –1<x<3}.  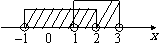   师:求并集时,两集合的相同元素如何在并集中表示.  生:遵循集合元素的互异性.  师:涉及不等式型集合问题.  注意利用数轴,运用数形结合思想求解.  生:在数轴上画出两集合,然后合并所有区间. 同时注意集合元素的互异性. |
学生尝试求解,老师适时适当指导,评析. 固化概念  提升能力 |
|
探究性质 |
①A∪A = A, ②A∪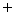 = A, = A, ③A∪B = B∪A,  ④ 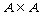 ∪B, ∪B,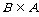 ∪B. ∪B. |
老师要求学生对性质进行合理解释. |
培养学生数学思维能力. |
|
形成概念 |
自学提要: ①由两集合的所有元素合并可得两集合的并集,而由两集合的公共元素组成的集合又会是两集合的一种怎样的运算?  ②交集运算具有的运算性质呢?  交集的定义.  由属于集合A且属于集合B的所有元素组成的集合,称为A与B的交集;记作A∩B,读作A交B.  即A∩B = {x | x∈A且x∈B}  Venn图表示  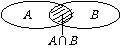  |
老师给出自学提要,学生在老师的引导下自我学习交集知识,自我体会交集运算的含义. 并总结交集的性质. 生:①A∩A = A;  ②A∩ 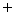 = =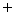 ; ; ③A∩B = B∩A;  ④A∩ 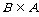 ,A∩ ,A∩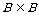 . . 师:适当阐述上述性质. |
自学辅导,合作交流,探究交集运算. 培养学生的自学能力,为终身发展培养基本素质. |
|
应用举例 |
例1 (1)A = {2,4,6,8,10}, B = {3,5,8,12},C = {8}.  (2)新华中学开运动会,设  A = {x | x是新华中学高一年级参加百米赛跑的同学},  B = {x | x是新华中学高一年级参加跳高比赛的同学},求A∩B. 例2 设平面内直线l1上点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示l1,l2的位置关系. |
学生上台板演,老师点评、总结. 例1 解:(1)∵A∩B = {8}, ∴A∩B = C. (2)A∩B就是新华中学高一年级中那些既参加百米赛跑又参加跳高比赛的同学组成的集合. 所以,A∩B = {x | x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}. 例2 解:平面内直线l1,l2可能有三种位置关系,即相交于一点,平行或重合. (1)直线l1,l2相交于一点P可表示为 L1∩L2 = {点P}; (2)直线l1,l2平行可表示为 L1∩L2 = 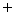 ; ;(3)直线l1,l2重合可表示为 L1∩L2 = L1 = L2. |
提升学生的动手实践能力. |
|
归纳总结 |
并集:A∪B = {x | x∈A或x∈B} 交集:A∩B = {x | x∈A且x∈B} 性质:①A∩A = A,A∪A = A, ②A∩ 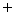 = =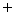 ,A∪ ,A∪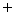 = A, = A,③A∩B = B∩A,A∪B = B∪A. |
学生合作交流:回顾→反思→总理→小结 老师点评、阐述 |
归纳知识、构建知识网络 |
|
课后作业 |
1.1第三课时 习案 |
学生独立完成 |
巩固知识,提升能力,反思升华 |
备选例题
例1 已知集合A = {–1,a2 + 1,a2 – 3},B = {– 4,a – 1,a + 1},且A∩B = {–2},求a的值.
[解析]法一:∵A∩B = {–2},∴–2∈B,
∴a – 1 = –2或a + 1 = –2,
解得a = –1或a = –3,
当a = –1时,A = {–1,2,–2},B = {– 4,–2,0},A∩B = {–2}.
当a = –3时,A = {–1,10,6},A不合要求,a = –3舍去
∴a = –1.
法二:∵A∩B = {–2},∴–2∈A,
又∵a2 + 1≥1,∴a2 – 3 = –2,
解得a =±1,
当a = 1时,A = {–1,2,–2},B = {– 4,0,2},A∩B≠{–2}.
当a = –1时,A = {–1,2,–2},B = {– 4,–2,0},A∩B ={–2},∴a = –1.
例2 集合A = {x | –1<x<1},B = {x | x<a},
(1)若A∩B =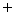 ,求a的取值范围;
,求a的取值范围;
(2)若A∪B = {x | x<1},求a的取值范围.
[解析](1)如下图所示:A = {x | –1<x<1},B = {x | x<a},且A∩B=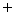 ,
,
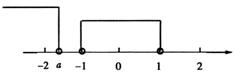
∴数轴上点x = a在x = – 1左侧.
∴a≤–1.
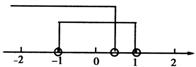 (2)如右图所示:A = {x | –1<x<1},B = {x | x<a}且A∪B = {x | x<1},
(2)如右图所示:A = {x | –1<x<1},B = {x | x<a}且A∪B = {x | x<1},
∴数轴上点x = a在x = –1和x = 1之间.
∴–1<a≤1.
 例3 已知集合A = {x | x2 – ax + a2 – 19 =
0},B = {x | x2 – 5x + 6 = 0},C = {x | x2 + 2x – 8 = 0},求a取何实数时,A∩B
例3 已知集合A = {x | x2 – ax + a2 – 19 =
0},B = {x | x2 – 5x + 6 = 0},C = {x | x2 + 2x – 8 = 0},求a取何实数时,A∩B 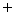 与A∩C =
与A∩C =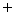 同时成立?
同时成立?
[解析]B = {x | x2 – 5x + 6 = 0} = {2,3},C = {x | x2 + 2x – 8 = 0} = {2,– 4}.
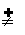 由A∩B
由A∩B 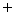 和A∩C =
和A∩C =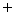 同时成立可知,3是方程x2 – ax + a2 – 19 = 0的解. 将3代入方程得a2 – 3a – 10 = 0,解得a = 5或a = –2.
同时成立可知,3是方程x2 – ax + a2 – 19 = 0的解. 将3代入方程得a2 – 3a – 10 = 0,解得a = 5或a = –2.
当a = 5时,A = {x | x2 – 5x + 6 = 0} = {2,3},此时A∩C = {2},与题设A∩C =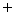 相矛盾,故不适合.
相矛盾,故不适合.
 当a = –2时,A = {x | x2 + 2x – 15 = 0} = {3,5},此时A∩B
当a = –2时,A = {x | x2 + 2x – 15 = 0} = {3,5},此时A∩B 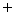 与A∩C =
与A∩C =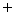 ,同时成立,∴满足条件的实数a = –2.
,同时成立,∴满足条件的实数a = –2.
例4 设集合A = {x2,2x – 1,– 4},B = {x – 5,1 – x,9},若A∩B = {9},求A∪B.
[解析]由9∈A,可得x2 = 9或2x – 1 = 9,解得x =±3或x = 5.
当x = 3时,A = {9,5,– 4},B = {–2,–2,9},B中元素违背了互异性,舍去.
当x = –3时,A = {9,–7,– 4},B = {–8,4,9},A∩B = {9}满足题意,故A∪B = {–7,– 4,–8,4,9}.
当x = 5时,A = {25,9,– 4},B = {0,– 4,9},此时A∩B = {– 4,9}与A∩B = {9}矛盾,故舍去.
综上所述,x = –3且A∪B = {–8,– 4,4,–7,9}.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com