9．“当日之冲(指日、地、月三星一线)，光常不合者，蔽于地也，是谓暗虚，在星则星微，遇月则食。”这一记载，最早有可能是在

A．《春秋》中　 　B．《史记》中　 　C．《汉书》中　 　D．《后汉书》中

8．《资治通鉴》记载：(西汉初期)“往往入盗汉边，不可胜数；然尚贪乐关市(指边境贸易)，嗜汉财物，汉亦关市不绝，以中其意。”这反映的是

A．汉朝与匈奴族的关系　　　　 B． 汉朝与西域各族的关系 　　　

C．汉朝与西南夷的关系　　 　　D．汉朝与朝鲜的关系　

7．据《汉书》记载，汉武帝时，某一官员“周行郡国，省察治状，黜陟能否，断治冤狱······”这一官员

A．级别不高，但可代表中央监察诸侯王和地方高官　　　

B．级别不高，但能代表中央执掌地方军政大权　　　

C．级别不高，不能监察诸侯王，只能监察地方官　　　　　　　　　

D．级别不高，不能代表中央监察诸侯王和地方高官

6. 秦朝徭役繁重，筑长城是其表现之一，古时即有孟姜女哭长城的传说故事以示控诉。为纪念孟姜女，山海关被后人定为哭长城之地，并盖有姜女庙。从秦朝的疆域图看，孟姜女哭长城的故事

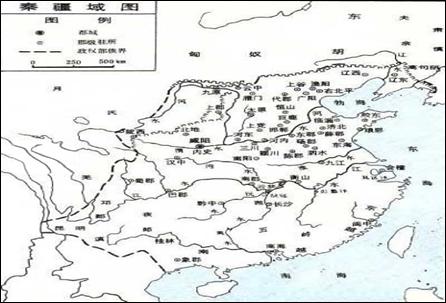
A．时间错误　　　 B. 地点错误　　　 C. 人物错误　　 　　D.　 情节错误

5. 2007年9月28日举行的祭孔大典上，从《论语》中评选出几句经典名句作为北京奥运会的礼仪用语，你认为以下不适合入选的一句是

A. “己所不欲，勿施于人” B. “四海之内皆兄弟也”　

C. “德不孤，必有邻”　　　 D. “非礼勿视，非礼勿听，非礼勿言，非礼勿动”　

4. “画野分民乱井田，百王礼乐散寒烟”所产生的重大影响是

A. 铁器大量使用，牛耕逐步推广　　　 B. 农业、手工业获得空前发展　　　　 C. 封建制度逐步得以确立　　　 　　　　　　D. 商人的政治地位显著提高　　　

3. 司马迁说：“(齐)桓公之盛，修善政以为诸侯会盟，称伯。”与之相关的史实正确的是

A. 桓公“修善政”的核心是“尊王攘夷”　 　

B. 此会盟发生在“城濮之战”大败楚军以后　　

C. 周王室派代表参加了会盟，并被迫承认“田氏代齐”　　　　

D. 此会盟发生地在今河南境内，桓公确立中原的霸主地位　

2. 2000年11月9日，《夏商周年表》正式公布，把我国的历史纪年由原来的“共和元年”向前延伸了1200多年。据此判断，“共和元年”发生的历史事件应是

A. 武王伐纣 　　B. 国人暴动　 　C. 犬戎攻破镐京　　 D. 周平王迁都洛邑

(三)简单的线性规划问题

问题：设P＝2x+y，式中变量x、y满足下列条件，求P的最大值和最小值。

首先，作出线性约束条件所表示的平面区域，这一区域称为可行区域；

其次，考虑目标P＝2x+y的几何意义；

第三，设P＝0，画出直线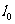；观察、分析，平移直线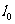，从而找到最优解；

最后，求得目标函数的最大值及最小值。

1. 基本概念：目标函数，线性目标函数线性规划问题，可行解，可行域，最优解：

诸如上述问题中，不等式组是一组对变量x、y的约束条件，由于这组约束条件都是关于x、y的一次不等式，所以又可称其为线性约束条件。P＝2x+y是欲达到最大值或最小值所涉及的变量x、y的解析式，我们把它称为目标函数。由于P＝2x+y又是关于x、y的一次解析式，所以又可叫做线性目标函数。

一般地，求线性目标函数在线性约束条件下的最大值或最小值的问题，统称为线性规划问题。那么，满足线性约束条件的解(x，y)叫做可行解，由所有可行解组成的集合叫做可行域。在上述问题中，可行域就是阴影部分表示的三角形区域。其中可行解(5，2)和(1，1)分别使目标函数取得最大值和最小值，它们都叫做这个问题的最优解。

2. 求线性目标函数在线性约束条件下的最优解的格式与步骤：

(1)寻找线性约束条件，线性目标函数；

(2)由二元一次不等式表示的平面区域做出可行域；

(3)在可行域内求目标函数的最优解。

[典型例题]

例1. 已知x、y满足不等式组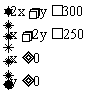，试求z＝300x+900y取最大值时的整点的坐标，及相应的z的最大值。

分析：先画出平面区域，然后在平面区域内寻找使z＝300x+900y取最大值时的整点。

解：如图所示平面区域AOBC，点A(0，125)，点B(150，0)，点C的坐标由方程组

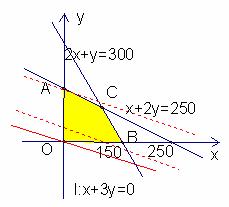
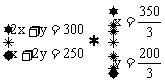
得C()，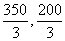

令t＝300x+900y，

即y＝－，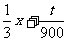

欲求z＝300x+900y的最大值，即转化为求截距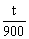的最大值，从而可求t的最大值，　 因直线y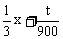＝－与直线y＝－x平行，故作y＝－x的平行线，当过点A(0，125)时，对应的直线的截距最大，所以此时整点A使z取最大值，z_max＝300×0+900×125＝112500。

例2. 求z＝600x+300y的最大值，使式中的x，y满足约束条件的整数值。

分析：画出约束条件表示的平面区域即可行域再解。

解：可行域如图所示：

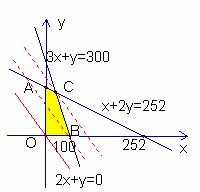
四边形AOBC，易求点A(0，126)，B(100，0)由方程组：

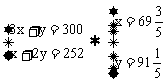
得点C的坐标为(69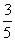，91)

因题设条件要求整点(x，y)使z＝600x+300y取最大值，将点(69，91)，(70，90)代入z＝600x+300y，可知当时，z取最大值为z_max＝600×70+300×900＝69000。

例3. 已知x、y满足不等式，求z＝3x+y的最小值。

分析：可先找出可行域，平行移动直线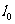：3x+y＝0，找出可行解，进而求出目标函数的最小值。

解：不等式x+2y≥2，表示直线x+2y＝2上及右上方的点的集合；

不等式2x+y≥1表示直线2x+y＝1上及右上方的点的集合。

可行域如图所示：

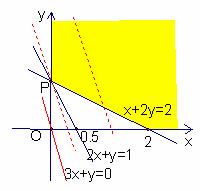
作直线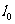：3x+y＝0，作一组与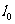直线平行的直线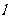：3x+y＝t，(t∈R)。

∵x、y是上面不等式组表示的区域内的点的坐标。

由图可知：

当直线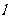：3x+y＝t通过P(0，1)时，t取到最小值1，即z_min＝1。

评述：简单线性规划问题就是求线性目标函数在线性约束条件下的最优解，无论此类题目是以什么实际问题提出，其求解的格式与步骤是不变的：

(1)寻找线性约束条件，线性目标函数；

(2)由二元一次不等式表示的平面区域做出可行域；

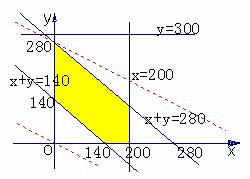
例4. 已知甲、乙两煤矿每年的产量分别为200万吨和300万吨，需经过东车站和西车站两个车站运往外地。东车站每年最多能运280万吨煤，西车站每年最多能运360万吨煤，甲煤矿运往东车站和西车站的运费价格分别为1元/吨和1.5元/吨，乙煤矿运往东车站和西车站的运费价格分别为0.8元/吨和1.6元/吨。煤矿应怎样编制调运方案，能使总运费最少?

解：设甲煤矿向东车站运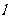万吨煤，乙煤矿向东车站运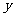万吨煤，那么总运费　　　　　　 z＝x+1.5(200－x)+0.8y+1.6(300－y)(万元)。即z＝780－0.5x－0.8y。

x、y应满足：

作出上面的不等式组所表示的平面区域。

设直线x+y＝280与y轴的交点为M，则M(0，280)。

把直线l：0.5x+0.8y＝0向上平移至经过平面区域上的点M时，z的值最小。

∵点M的坐标为(0，280)，

∴甲煤矿生产的煤全部运往西车站，乙煤矿向东车站运280万吨，向西车站运20万吨时，总运费最少。

[模拟试题](答题时间：25分钟)

1. 画出不等式组表示的平面区域。

2. 求z＝2x+y的最大值，使式中的x、y满足约束条件

3. 求z＝3x+5y的最大值和最小值，使式中x、y 满足约束条件

4. 某纺纱厂生产甲、乙两种棉纱，已知生产甲种棉纱1吨需耗一级子棉2吨、二级子棉1吨；生产乙种棉纱需耗一级子棉1吨、二级子棉2吨，每1吨甲种棉纱的利润是600元，每1吨乙种棉纱的利润是900元，工厂在生产这两种棉纱的计划中要求消耗一级子棉不超过300吨、二级子棉不超过250吨。甲、乙两种棉纱应各生产多少(精确到吨)，能使利润总额最大？

5. 要将甲、乙两种长短不同的钢管截成A、B、C三种规格，每根钢管可同时截得三种规格的短钢管的根数如下表所示：

今需A、B、C三种规格的钢管各13、16、18根，问各截这两种钢管多少根可得所需三种规格钢管，且使所用钢管根数最少。