
1. 新华社2007年7月29日报道,美国研究人员在黄石国家公园发现了一种罕见细菌,它们能像绿色植物一样把光能转化成维持自身生存的生物能。这种细菌嗜热,属于酸杆菌,这种细菌长有许多触角,叫做集光绿色体。每个触角含有大量叶绿素,正是这些叶绿素使得细菌能够在菌苔上同其他细菌争夺阳光,维持生存。这种细菌是人们迄今发现的第一种含有集光绿色体的好氧微生物。下列有关该菌的叙述,正确的是( )
A.该菌的基本结构包括细胞壁、细胞膜、细胞质和细胞核,用纤维素酶可破坏细胞壁
B.高倍显微镜下可观察到该菌的遗传物质分布于细胞核内,进行二分裂生殖
C.该菌是好氧细菌,其生命活动所需能量主要由线粒体提供 
D.培养该细菌的培养基可以不含碳源,该细菌在生态系统中属于生产者
22. (本小题满分12分)已知点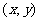 在椭圆C:
在椭圆C: 的第一象限上运动
的第一象限上运动
(1) 求点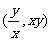 的轨迹
的轨迹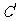 方程
方程
(2) 若把轨迹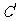 的方程表达式记为
的方程表达式记为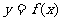 ,且在
,且在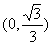 内
内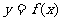 有最大值,试求椭圆C的离心率的取值范围
有最大值,试求椭圆C的离心率的取值范围
21.(本小题满分12分)P是抛物线C: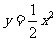 上一点,直线
上一点,直线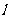 过点P并与抛物线C在点P的切线垂直,
过点P并与抛物线C在点P的切线垂直,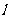 与抛物线C相交于另一点Q
与抛物线C相交于另一点Q
(1)当点P的横坐标为2时,求直线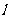 的方程;
的方程;
(2)当点P在抛物线C上移动时,求线段PQ中点M的轨迹方程,并求点M到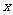 轴的最短距离。
轴的最短距离。
20.(本小题满分12分)已知数列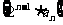 的前
的前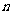 项和
项和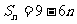
(1) 求数列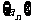 的通项公式;
的通项公式;
(2) 设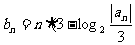 ),求数列
),求数列 的前
的前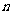 项和。
项和。
19.(本小题满分12分)已知平行六面体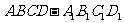 的底面
的底面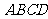 是矩形,且侧面
是矩形,且侧面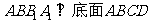
 ,
,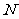 是
是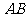 上一点,
上一点,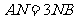 ,
, 的中点,F是EC中点 , E为AB中点,
的中点,F是EC中点 , E为AB中点,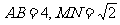 ,侧棱与底面
,侧棱与底面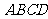 成
成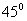 角.
角.
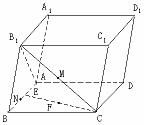 (1)求证:
(1)求证: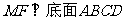
(2)求二面角M-AB-C的大小
(3)求MN与平面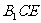 所成角的大小。
所成角的大小。
18.(本小题满分12分)设每次试验为同时抛掷三枚同样的硬币,若其中出现了正面,则称该次试验成功,现作了10次重复独立试验。
求(1)10次重复独立试验中至少成功一次的概率
(2)10次重复独立试验中成功次数的数学期望和方差









17.(本小题满分10分) 中,
中,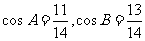

(1)求角C
(2)若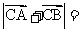
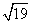 ,求AB的长
,求AB的长













16.给出下列命题:
①
若m α,n
α,n α,m∥β,n∥β,则α∥β。
α,m∥β,n∥β,则α∥β。
②
函数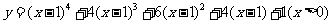 的反函数为
的反函数为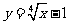

③
A、B、C、D四人中,调换其中三人的座位,不同的调换方法有8种。
④
α、β、γ为三个不同的平面,且α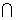 β=L。若α⊥γ,β⊥γ,则L⊥γ
β=L。若α⊥γ,β⊥γ,则L⊥γ
其中正确命题的序号是
.
15.

 中
中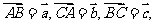 当
当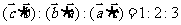 时,则
时,则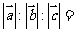

14. 设O为坐标原点,M
设O为坐标原点,M ,N
,N 满足
满足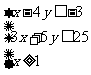 ,则
,则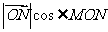 的最大值为 .
的最大值为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com