
7. 火车轨道在转弯处外轨高于内轨,其高度差由转弯半径与火车速度确定.若在某转弯处规定行驶的速度为v,则下列说法中正确的是
①当火车以v的速度通过此弯路时,火车所受重力与轨道面支持力的合力提供向心力
②当火车以v的速度通过此弯路时,火车所受重力、轨道面支持力和外轨对轮缘弹力的合力提供向心力
③当火车速度大于v时,轮缘挤压外轨 ④当火车速度小于v时,轮缘挤压外轨
A.①③ B.①④ C.②③ D.②④
6.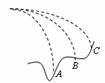 在同一点O抛出的三个物体,做平抛运动的轨迹如图所示,则三个体做平抛运动的初速度vA、vB、vC的关系和三个物体做平抛运动的时间tA、tB、tC的关系分别是
在同一点O抛出的三个物体,做平抛运动的轨迹如图所示,则三个体做平抛运动的初速度vA、vB、vC的关系和三个物体做平抛运动的时间tA、tB、tC的关系分别是
A.vA>vB>vC,tA>tB>tC B.vA=vB=vC,tA=tB=tC
C.vA<vB<vC,tA>tB>tC D.vA>vB>vC,tA<tB<tC
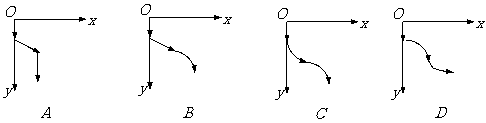
5. 一物体由静止开始自由下落,一小段时间后突然受一恒定水平向右的风力的影响,但着地前一段时间风突然停止,则其运动的轨迹可能是图中的哪一个?
4.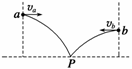 如图所示,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两抛出点水平距离相等的P点.若不计空气阻力,下列关系式正确的是
如图所示,在同一竖直面内,小球a、b从高度不同的两点,分别以初速度va和vb沿水平方向抛出,经过时间ta和tb后落到与两抛出点水平距离相等的P点.若不计空气阻力,下列关系式正确的是
A.ta>tb,va<vb B.ta>tb,va>vb
C.ta<tb,va<vb ? D.ta<tb,va>vb
3.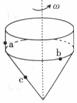 图所示是一个玩具陀螺。a、b和c是陀螺上的三个点。当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是
图所示是一个玩具陀螺。a、b和c是陀螺上的三个点。当陀螺绕垂直于地面的轴线以角速度ω稳定旋转时,下列表述正确的是
A.a、b和c三点的线速度大小相等 B.a、b和c三点的角速度相等
C.a、b的角速度比c的大 D.c的线速度比a、b的大
2.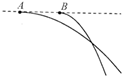 在同一水平直线上的两位置分别沿同方向抛出两小球
在同一水平直线上的两位置分别沿同方向抛出两小球 和
和 ,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须
,其运动轨迹如图所示,不计空气阻力.要使两球在空中相遇,则必须
A.甲先抛出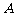 球 B.先抛出
球 B.先抛出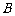 球
球
C.同时抛出两球 D.使两球质量相等
个选项是正确的)
1. 右图为一种早期的自行车,这种下带链条传动的自行车前轮的直径很大,这样的设计在当时主要是为了
右图为一种早期的自行车,这种下带链条传动的自行车前轮的直径很大,这样的设计在当时主要是为了
A.提高速度 B.提高稳定性
C.骑行方便 D.减小阻力
|
教学环节 |
教学内容 |
师生互动 |
设计意图 |
回顾反思 构建体系 |
函数性质单元知识网络 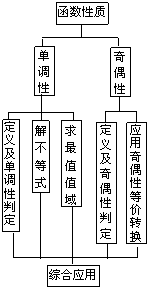  |
生:借助课本.并回顾学习过程. 整理函数掌握函数的有关性质归纳知识的纵横联系. 师生合作:学生口述单元基本知识及相互联系,老师点评、阐述、板书网络图. |
整理知识,培养归纳能力.  形成知识网络系统. |
经典例题 剖 析  升华能力 |
  例1试讨论函数f (x) = 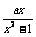 ,x(–1,1)的单调性(其中a≠0). ,x(–1,1)的单调性(其中a≠0).          例2 试计论并证明函数y = f (x) = x +  (a>0)在定义域上的单调性,函数在(0,+∞)上是否有最小值? (a>0)在定义域上的单调性,函数在(0,+∞)上是否有最小值?                       例3 已知f (x)是定义在(0,+∞)上的增函数,且满足f (xy) =  f (x) + f (y),f (2) =1.  (1)求证:f (8) =3;  (2)解不等式  f (x) – f (x–2) >3.      例4 已知函数f (x),当x、y∈R时,恒有f (x + y) = f (x) + f ( y).  (1)求证:f (x)是奇函数;  (2)如果x∈R+ ,f (x)<0,并且f (1) = 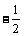 ,试求f (x)在区间[–2,6]上的最值. ,试求f (x)在区间[–2,6]上的最值. |
师生合作:学生独立尝试完成例1 ~ 例4并由学生代表板书解答过程. 老师点评. 师生共同小结解题思络. 例1[解析]设–x<x1<x2<1, 即△x = x2–x1>0, 则△y = f (x2) – f (x2) = = ∵–1<x1<x2<1, ∴x1–x2<0,–1<0,–1<0. |x1x2|<1,即 –1<x1x2<1,x1x2 +1>0, ∴<0. 因此,当a>0时,△y = f (x2) – f (x1)<0, 即f (x1)>f (x2),此时函数为减函数; 当a<0时,△y = f (x2) – f (x1) >0, 即f (x1)<f (x2),此时函数为增函数. 例2[解析]函数y = x +(a>0)在区间(–∞,–)上是增函数,在区间[–,0]上是减函数,在区间 (0,]上是减函数,在区间(,+∞)上是增函数. 先证明y = x +(a>0)在(0,+∞)上的增减性, 任取0<x1<x2, 则△x = x1–x2<0, △y = f (x1) – f (x2) = (x1 +) – (x2 +) = (x1–x2) + (–) = (x1–x2) + = (x1–x2) (1–) =△x. ∵0<x1<x2, ∴△x = x1–x2<0,x1x2>0. (1)当x1,x2∈(0,)时,0<x1x2<a,∴x1x2 – a<0, 此时①>0时, △y = f (x1) – f (x2)>0, ∴f (x)在(0,  )上是减函数. )上是减函数.(2)当x1,x2∈[  ,+∞)时,x1x2>a,∴x1x2 –
a>0, ,+∞)时,x1x2>a,∴x1x2 –
a>0,此时①<0,△y= f (x1) – f (x2)<0, ∴f (x)在[  ,+∞)上是增函数, ,+∞)上是增函数,同理可证函数f (x)在(–∞,–  )上为增函数, )上为增函数,在[–  ,0)上为减函数. ,0)上为减函数.由函数f (x) = x + 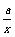 在[0, 在[0, )上为减函数,且在[ )上为减函数,且在[ ,+∞)上为增函数知道,f (x)≥f ( ,+∞)上为增函数知道,f (x)≥f ( ) =2 ) =2 ,其中x∈(0,+ ∞), ,其中x∈(0,+ ∞),∴f (x)min=2  , ,也可以配方求f (x) = x + 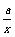 (a>0)在(0,+∞)上的最小值, (a>0)在(0,+∞)上的最小值,∴f (x) = x + 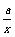 = ( = (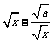 )2 + 2 )2 + 2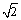 , ,当且仅当x =  时,f (x)min =2 时,f (x)min =2 . .例3[解析](1)在f (xy) = f (x) + f (y)中, 设x = y =2,则有f (4)=f (2)+f (2), 设x= 4,y =2, 则有f (8) = f (4) + f (2) =3 f (2) = 3. (2)由f (x) – f (x–2)>3, 得f (x)>f (8) + f (x–2) = f [8 (x–2)], ∵f (x) 是(0,+∞)上的增函数, ∴ 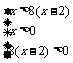 ,解得2<x< ,解得2<x<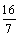 , ,故原不等式的解集为{x|2<x< 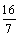 }. }.例4[解析](1)∵函数定义域为R,其定义域关于原点对称, ∵f (x + y) = f (x) + f ( y), 令y = –x,x、– x∈R, 代入f (x + y) = f (x) + f ( y), ∴f (0) = f (0) + f (0),得f (0) = 0, ∴f (x) + f (–x) = 0,得 f (–x) = – f (x), ∴f (x)为奇函数. (2)设x、y∈R+, ∵f (x+y) = f (x) + f ( y), ∴f (x+y) – f (x) = f ( y), ∵x∈R+,f (x)<0, ∴f (x+y) – f (x)<0, ∴f (x+y)<f (x). ∵x+y<x, ∴f (x)在(0,+∞)上是减函数. 又∵f (x)为奇函数, f (0) = 0, ∴f (x)在(–∞,+∞)上是减函数. ∴在区间[–2,6]上f (–2)为最大值,f (6)为最小值. ∵f (1) = 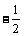 , ,∴f (–2)= – f (2) = –2 f (1) =1, f (6) = 2 f (3)=2[ f (1) + f (2)] = –3, ∴f (x)在区间[–2,6]上的最大值为1,最小值为–3. |
动手尝试练习,培养并提高解题能力. |
备选例题
例1 用定义证明函数y = f (x) =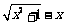 是减函数.
是减函数.
[解析]∵x2 +1>0对任意实数x均成立,
∴函数y = f
(x) =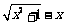 的定义域是R,
的定义域是R,
任取x1、x2∈R,且x1<x2,则△x = x2–x1>0,
△y = f (x2) – f (x1)
=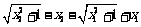
=
=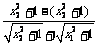 – (x2–x1)
– (x2–x1)
=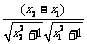 (x2
+ x1–
(x2
+ x1–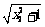 –
–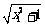 ),
),
∵x1∈R,x2∈R,且x1<x2,
∴x2–x1>0,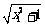 >
>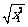 = |x1|≥x1,
= |x1|≥x1,
∴x1–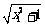 <0,同理x2–
<0,同理x2–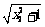 <0,
<0,
x1 + x2–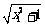 –
–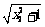 <0,
<0,
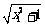 +
+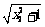 >| x1| + | x2 |>0,
>| x1| + | x2 |>0,
∴f (x2) – f (x1) <0,
∴y = f
(x) =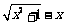 在R上是减函数.
在R上是减函数.
例2 已知函数f (x)的定义域为R,满足f (–x) =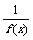 >0,且g (x) = f (x) + c(c为常数)在区间[a,b]上是减函数. 判断并证明g (x)在区间[– b,– a]上的单调性.
>0,且g (x) = f (x) + c(c为常数)在区间[a,b]上是减函数. 判断并证明g (x)在区间[– b,– a]上的单调性.
解析:设– b≤x1<x2≤– a,
则△x = x2 – x1>0,b≥–x1>–x2≥a,
∵g (x)在区间[a,b]上是减函数,
∴g (–x1)<g (–x2),即f (–x1) + c<f (–x2) + c,
则f (–x1)<f (–x2),又∵f (–x) =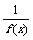 >0,
>0,
∴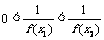 ,即f (x1)>f (x2)
,即f (x1)>f (x2)
∴f (x1) + c>f (x2) + c,即g (x1)>g(x2),
△y = g (x2) – g (x1)<0,
∴g (x)在区间[– b,– a]上是减函数.
动手练习与合作交流相结合. 在回顾、反思中整合知识,在综合问题探究、解答中提升能力. 加深对知识的准确、到位的理解与应用.
重点:整合知识、构建单元知识系统.
难点:提升综合应用能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com