
例1若f :y=3x+1是从集合A={1,2,3,k}到集合B={4,7,a4,a2+3a}的一个映射,求自然数a、k的值及集合A、B.(a=2,k=5;A={1,2,3,5}B={4,7,16,10})
例2、设函数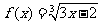 ,
,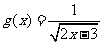 ,求函数
,求函数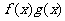 的定义域.{x|x>
的定义域.{x|x>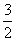 }
}
变式1: 函数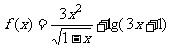 的定义域是
的定义域是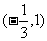
变式2:设 ,则
,则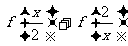 的定义域为
的定义域为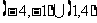
函数值域
观察法(用非负数的性质)
例1 求下列函数的值域:y=-3x2+2;{y|y≥2}
变式:y=5+2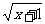 (x≥-1).{y|y≥5}
(x≥-1).{y|y≥5}
配方法
例2 求值域:y=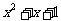
变式y=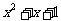 x
x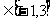
变式求函数y=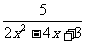 的值域.
的值域.
换元法
例3.求函数 的值域.
的值域.

变式求函数y=3x-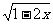 的值域.{y|y≤
的值域.{y|y≤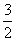 }
}
分离常数法
对某些分式函数,可通过分离常数法,化成部分分式来求值域.
例4
求下列函数的值域:y=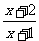 ({y|y
({y|y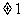 })
})
变式、y=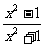 .
[-1,1]
.
[-1,1]
利用判别式
特殊地,对于可以化为关于x的二次方程a(y)x2+b(y)x+c(y)=0的函数y=f(x),可利用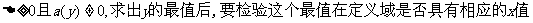 .
.
例5 求函数y =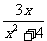 的最值.[-
的最值.[-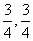 ]
]
变式: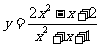 ;[1,5]
;[1,5]
函数解析式
8. 下列函数中值域为 的是(B)
的是(B)
(A) 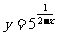 (B)
(B) 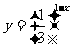 (C)
(C) 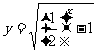 (D)
(D) 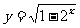
7. 求函数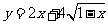 的值域
的值域 .
.
6.已知 (x¹0), 求
(x¹0), 求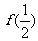 = 15
.
= 15
.
5. 若函数 的定义域为[-1,1],求函数
的定义域为[-1,1],求函数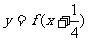
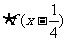 的定义域[-
的定义域[-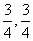 ]。
]。
4. 求函数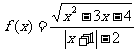 的定义域. {x|x≥3或-3<x≤-1或x>-3}
的定义域. {x|x≥3或-3<x≤-1或x>-3}
3.已知扇形的周长为20,半径为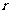 ,扇形面积为
,扇形面积为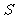 ,则
,则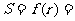 -r
-r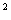 -20r;定义域为0<r<10。
-20r;定义域为0<r<10。
2. 设集合A和集合B都是自然数集合N,映射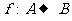 把集合A中的元素
把集合A中的元素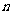 映射到集合B中的元素
映射到集合B中的元素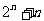 ,则在映射
,则在映射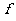 下,象20的原象是
4
下,象20的原象是
4
1.若 ,
,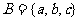 ,则
,则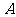 到
到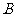 的映射有
3
的映射有
3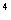 个,
个,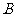 到
到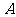 的映射有
4
的映射有
4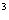 个;若
个;若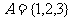 ,
,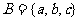 , 则
, 则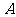 到
到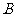 的一一映射有
6 个。
的一一映射有
6 个。
5.函数值域的求法:①配方法(二次或四次);②判别式法;③反函数法(反解法);④换元法(代数换元法);⑤不等式法;⑥单调函数法.
⑵常用函数的值域,这是求其他复杂函数值域的基础。
① 函数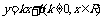 的值域为R;
的值域为R;
② 二次函数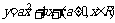
当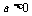 时值域是
时值域是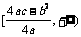 ,当
,当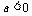 时值域是
时值域是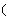

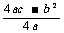 ];
];
③ 反比例函数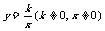 的值域为
的值域为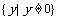 ;
;
④ 指数函数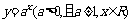 的值域为
的值域为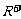 ;
;
⑤ 对数函数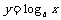
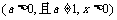 的值域为R;
的值域为R;
⑥ 函数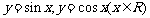 的值域为[-1,1];
的值域为[-1,1];
⑦ 函数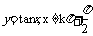 ,
,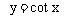
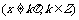 的值域为R;
的值域为R;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com